|
Order Isomorphic
In the mathematical field of order theory, an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets (posets). Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that either of the orders can be obtained from the other just by renaming of elements. Two strictly weaker notions that relate to order isomorphisms are order embeddings and Galois connections. Definition Formally, given two posets (S,\le_S) and (T,\le_T), an order isomorphism from (S,\le_S) to (T,\le_T) is a bijective function f from S to T with the property that, for every x and y in S, x \le_S y if and only if f(x)\le_T f(y). That is, it is a bijective order-embedding. It is also possible to define an order isomorphism to be a surjective order-embedding. The two assumptions that f cover all the elements of T and that it preserve orderings, are enough to ensure that f is also one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and mathematical analysis, analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of mathematical object, abstract objects and the use of pure reason to proof (mathematics), prove them. These objects consist of either abstraction (mathematics), abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of inference rule, deductive rules to already established results. These results include previously proved theorems, axioms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Interval
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \,\sim\, on S, the of an element a in S, denoted by is the set \ of elements which are equivalent to a. It may be proven, from the defining properties of equivalence relations, that the equivalence classes form a partition of S. This partition—the set of equivalence classes—is sometimes called the quotient set or the quotient space of S by \,\sim\,, and is denoted by S / \sim. When the set S has some structure (such as a group operation or a topology) and the equivalence relation \,\sim\, is compatible with this structure, the quotient set often inherits a similar structure from its parent set. Exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Relation
In mathematics, a relation on a set is transitive if, for all elements , , in , whenever relates to and to , then also relates to . Each partial order as well as each equivalence relation needs to be transitive. Definition A homogeneous relation on the set is a ''transitive relation'' if, :for all , if and , then . Or in terms of first-order logic: :\forall a,b,c \in X: (aRb \wedge bRc) \Rightarrow aRc, where is the infix notation for . Examples As a non-mathematical example, the relation "is an ancestor of" is transitive. For example, if Amy is an ancestor of Becky, and Becky is an ancestor of Carrie, then Amy, too, is an ancestor of Carrie. On the other hand, "is the birth parent of" is not a transitive relation, because if Alice is the birth parent of Brenda, and Brenda is the birth parent of Claire, then this does not imply that Alice is the birth parent of Claire. What is more, it is antitransitive: Alice can ''never'' be the birth parent of Claire. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Relation
A symmetric relation is a type of binary relation. An example is the relation "is equal to", because if ''a'' = ''b'' is true then ''b'' = ''a'' is also true. Formally, a binary relation ''R'' over a set ''X'' is symmetric if: :\forall a, b \in X(a R b \Leftrightarrow b R a) , where the notation aRb means that (a,b)\in R. If ''R''T represents the converse of ''R'', then ''R'' is symmetric if and only if ''R'' = ''R''T. Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation. Examples In mathematics * "is equal to" ( equality) (whereas "is less than" is not symmetric) * "is comparable to", for elements of a partially ordered set * "... and ... are odd": :::::: Outside mathematics * "is married to" (in most legal systems) * "is a fully biological sibling of" * "is a homophone A homophone () is a word that is pronounced the same (to varying extent) as another word but differs in meaning. A ''homophone'' may also dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflexive Relation
In mathematics, a binary relation ''R'' on a set ''X'' is reflexive if it relates every element of ''X'' to itself. An example of a reflexive relation is the relation " is equal to" on the set of real numbers, since every real number is equal to itself. A reflexive relation is said to have the reflexive property or is said to possess reflexivity. Along with symmetry and transitivity, reflexivity is one of three properties defining equivalence relations. Definitions Let R be a binary relation on a set X, which by definition is just a subset of X \times X. For any x, y \in X, the notation x R y means that (x, y) \in R while "not x R y" means that (x, y) \not\in R. The relation R is called if x R x for every x \in X or equivalently, if \operatorname_X \subseteq R where \operatorname_X := \ denotes the identity relation on X. The of R is the union R \cup \operatorname_X, which can equivalently be defined as the smallest (with respect to \subseteq) reflexive relation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes. Two elements of the given set are equivalent to each other if and only if they belong to the same equivalence class. Notation Various notations are used in the literature to denote that two elements a and b of a set are equivalent with respect to an equivalence relation R; the most common are "a \sim b" and "", which are used when R is implicit, and variations of "a \sim_R b", "", or "" to specify R explicitly. Non-equivalence may be written "" or "a \not\equiv b". Definition A binary relation \,\sim\, on a set X is said to be an equivalence relation, if and only if it is reflexive, symmetric and transitive. That is, for all a, b, and c in X: * a \sim a ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Composition
In mathematics, function composition is an operation that takes two functions and , and produces a function such that . In this operation, the function is applied to the result of applying the function to . That is, the functions and are composed to yield a function that maps in domain to in codomain . Intuitively, if is a function of , and is a function of , then is a function of . The resulting ''composite'' function is denoted , defined by for all in . The notation is read as " of ", " after ", " circle ", " round ", " about ", " composed with ", " following ", " then ", or " on ", or "the composition of and ". Intuitively, composing functions is a chaining process in which the output of function feeds the input of function . The composition of functions is a special case of the composition of relations, sometimes also denoted by \circ. As a result, all properties of composition of relations are true of composition of functions, such as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Mathematical Analysis And Applications
The ''Journal of Mathematical Analysis and Applications'' is an academic journal in mathematics, specializing in mathematical analysis and related topics in applied mathematics. It was founded in 1960, as part of a series of new journals on areas of mathematics published by Academic Press, and is now published by Elsevier. For most years since 1997 it has been ranked by SCImago Journal Rank The SCImago Journal Rank (SJR) indicator is a measure of the prestige of scholarly journals that accounts for both the number of citations received by a journal and the prestige of the journals where the citations come from. Rationale Citati ... as among the top 50% of journals in its topic areas. retrieved 2017 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
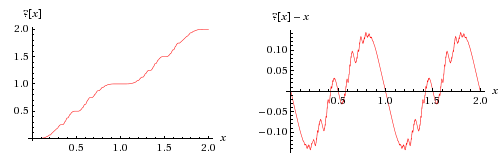
Minkowski's Question-mark Function
In mathematics, the Minkowski question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. It also maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree. Definition and intuition One way to define the question-mark function involves the correspondence between two different ways of representing fractional numbers using finite or infinite binary sequences. Most familiarly, a string of 0's and 1's with a single point mark ".", like "11.001001000011111..." can be interpreted as the binary representation of a number. In this case this number is 2+1+\frac18+\frac1+\cdots=\pi. There is a different way of interpreting the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Rational
In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number. The sum, difference, or product of any two dyadic rational numbers is another dyadic rational number, given by a simple formula. However, division of one dyadic rational number by another does not always produce a dyadic rational result. Mathematically, this means that the dyadic rational numbers form a ring, lying between the ring of integers and the field of rational numbers. This ring may be denoted \Z tfrac12/math>. In advanced mathematics, the dyadic rational numbers are central to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |