|
Oriented Surface
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
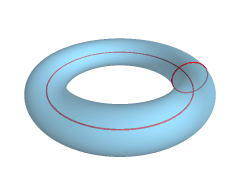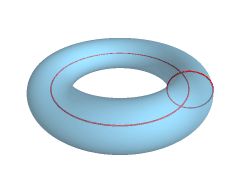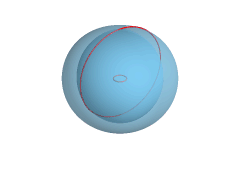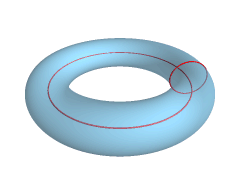
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a '' toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a ''solid torus'', which is form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifolds
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas (topology), atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is Differentiable function, differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homology (mathematics)
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry. The original motivation for defining homology groups was the observation that two shapes can be distinguished by examining their holes. For instance, a circle is not a disk because the circle has a hole through it while the disk is solid, and the ordinary sphere is not a circle because the sphere encloses a two-dimensional hole while the circle encloses a one-dimensional hole. However, because a hole is "not there", it is not immediately obvious how to define a hole or how to distinguish different kinds of holes. Homology was originally a rigorous mathematical method for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulation (topology)
In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling. Motivation On the one hand, it is sometimes useful to forget about superfluous information of topological spaces: The replacement of the original spaces with simplicial complexes may help to recognize crucial properties and to gain a better understanding of the considered object. On the other hand, simplicial complexes are objects of combinatorial character and therefore one can assign them quantities rising from their combinatorial pattern, for instance, the Euler characteristic. Triangulation allows now to assign such quantities to topological spaces. Investigations concerning the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Immersion (mathematics)
In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential (or pushforward) is everywhere injective. Explicitly, is an immersion if :D_pf : T_p M \to T_N\, is an injective function at every point ''p'' of ''M'' (where ''TpX'' denotes the tangent space of a manifold ''X'' at a point ''p'' in ''X''). Equivalently, ''f'' is an immersion if its derivative has constant rank equal to the dimension of ''M'': :\operatorname\,D_p f = \dim M. The function ''f'' itself need not be injective, only its derivative must be. A related concept is that of an embedding. A smooth embedding is an injective immersion that is also a topological embedding, so that ''M'' is diffeomorphic to its image in ''N''. An immersion is precisely a local embedding – that is, for any point there is a neighbourhood, , of ''x'' such that is an embedding, and conversely a local embedding is an immersion. For infinite dimensional manifolds, this is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein Bottle
In topology, a branch of mathematics, the Klein bottle () is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined. Informally, it is a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. Other related non-orientable objects include the Möbius strip and the real projective plane. While a Möbius strip is a surface with boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary. The concept of a Klein bottle was first described in 1882 by the German mathematician Felix Klein. Construction The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagrams below. Note that this is an "abstract" gluing in the sense that trying to rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Projective Plane
In mathematics, the real projective plane is an example of a compact non- orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in passing through the origin. The plane is also often described topologically, in terms of a construction based on the Möbius strip: if one could glue the (single) edge of the Möbius strip to itself in the correct direction, one would obtain the projective plane. (This cannot be done in three-dimensional space without the surface intersecting itself.) Equivalently, gluing a disk along the boundary of the Möbius strip gives the projective plane. Topologically, it has Euler characteristic 1, hence a demigenus (non-orientable genus, Euler genus) of 1. Since the Möbius strip, in turn, can be constructed from a square by g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a '' toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a ''solid torus'', which is form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (mathematics)
In mathematics, a plane is a Euclidean ( flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Normal
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one (a unit vector) or its length may represent the curvature of the object (a '' curvature vector''); its algebraic sign may indicate sides (interior or exterior). In three dimensions, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality ( right angles). The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphic
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word ''homeomorphism'' comes from the Greek words '' ὅμοιος'' (''homoios'') = similar or same and '' μορφή'' (''morphē'') = shape or form, introduced to mathematics by Henri Poincaré in 1895. Very roughly speaking, a topological space is a geometric object, and the homeomorphism is a continuous stretching and bending of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |