|
Octupole
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angular features ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity ( stress–energy tensor, cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Harmonics
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. Since the spherical harmonics form a complete set of orthogonal functions and thus an orthonormal basis, each function defined on the surface of a sphere can be written as a sum of these spherical harmonics. This is similar to periodic functions defined on a circle that can be expressed as a sum of circular functions (sines and cosines) via Fourier series. Like the sines and cosines in Fourier series, the spherical harmonics may be organized by (spatial) angular frequency, as seen in the rows of functions in the illustration on the right. Further, spherical harmonics are basis functions for irreducible representations of SO(3), the group of rotations in three dimensions, and thus play a central role in the group theoretic discussion of SO(3). Spherical harmonics originate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
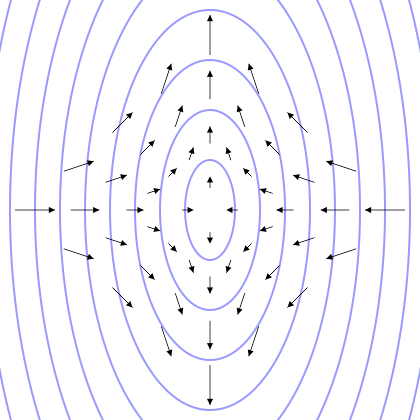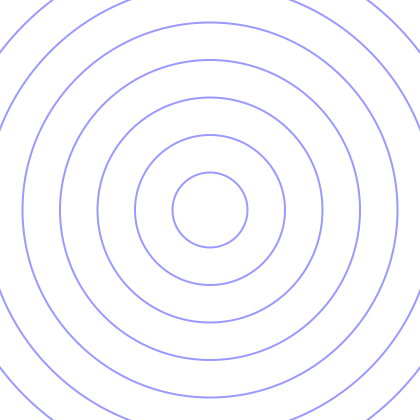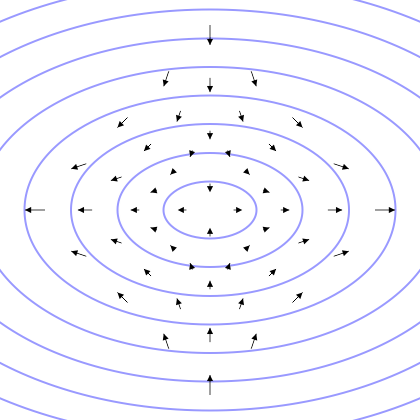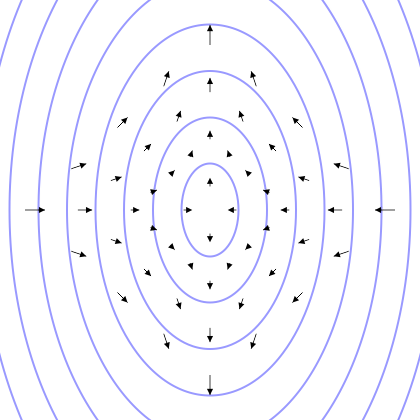
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity. Mathematical definition The quadrupole moment tensor ''Q'' is a rank-two tensor—3×3 matrix. There are several definitions, but it is normally stated in the traceless form (i.e. Q_ + Q_ + Q_ = 0). The quadrupole moment tensor has thus nine components, but because of transposition symmetry and Trace (linear algebra), zero-trace property, in this form only five of these are independent. For a discrete system of \ell point charges or masses in the case of a Quadrupole#Gravitational quadrupole, gravitational quadrupole, each with charge q_\ell, or mass m_\ell, and position \vec_\ell = \left(r_, r_, r_\right) relative to the coordinate system origin, the components of the ''Q'' matrix are defined by: : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\[1ex] & = \underbrace_ \times \underbrace_ \\[1ex] & = b^n \times b^m \end In other words, when multiplying a base raised to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes E-field) is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions (also called forces) of nature. Electric fields are important in many areas of physics, and are exploited in electrical technology. In atomic physics and chemistry, for instance, the electric field is the attractive force holding the atomic nucleus and electrons together in atoms. It is also the force responsible for chemical bonding between atoms that result in molecules. The electric field is defined as a vector field that associates to each point in space the electrostatic ( Coulomb) for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.. Definition The Laurent series for a complex function f(z) about a point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where a_n and c are constants, with a_n defined by a line integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic (analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in red ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Wave
Gravitational waves are waves of the intensity of gravity generated by the accelerated masses of an orbital binary system that propagate as waves outward from their source at the speed of light. They were first proposed by Oliver Heaviside in 1893 and then later by Henri Poincaré in 1905 as waves similar to electromagnetic waves but the gravitational equivalent. Gravitational waves were later predicted in 1916 by Albert Einstein on the basis of his general theory of relativity as ripples in spacetime. Later he refused to accept gravitational waves. Gravitational waves transport energy as gravitational radiation, a form of radiant energy similar to electromagnetic radiation. Newton's law of universal gravitation, part of classical mechanics, does not provide for their existence, since that law is predicated on the assumption that physical interactions propagate instantaneously (at infinite speed)showing one of the ways the methods of Newtonian physics are unable to explain ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a ''scalar potential'', which is a scalar field whose gradient is a given vector field. Formally, given a vector field v, a ''vector potential'' is a C^2 vector field A such that \mathbf = \nabla \times \mathbf. Consequence If a vector field v admits a vector potential A, then from the equality \nabla \cdot (\nabla \times \mathbf) = 0 (divergence of the curl is zero) one obtains \nabla \cdot \mathbf = \nabla \cdot (\nabla \times \mathbf) = 0, which implies that v must be a solenoidal vector field. Theorem Let \mathbf : \R^3 \to \R^3 be a solenoidal vector field which is twice continuously differentiable. Assume that decreases at least as fast as 1/\, \mathbf\, for \, \mathbf\, \to \infty . Define \mathbf (\mathbf) = \frac \int_ \frac \, d^3\mathbf. Then, A is a vector potential for , that is, \nabla \times \mathbf =\mathbf. Here, \nabla_y \times ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (mathematics)
A scalar is an element of a field which is used to define a ''vector space''. In linear algebra, real numbers or generally elements of a field are called scalars and relate to vectors in an associated vector space through the operation of scalar multiplication (defined in the vector space), in which a vector can be multiplied by a scalar in the defined way to produce another vector. Generally speaking, a vector space may be defined by using any field instead of real numbers (such as complex numbers). Then scalars of that vector space will be elements of the associated field (such as complex numbers). A scalar product operation – not to be confused with scalar multiplication – may be defined on a vector space, allowing two vectors to be multiplied in the defined way to produce a scalar. A vector space equipped with a scalar product is called an inner product space. A quantity described by multiple scalars, such as having both direction and magnitude, is called a '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |