|
Normalizing Flow
A flow-based generative model is a generative model used in machine learning that explicitly models a probability distribution by leveraging normalizing flow, which is a statistical method using the Probability density function#Function of random variables and change of variables in the probability density function, change-of-variable law of probabilities to transform a simple distribution into a complex one. The direct modeling of likelihood provides many advantages. For example, the negative log-likelihood can be directly computed and minimized as the loss function. Additionally, novel samples can be generated by sampling from the initial distribution, and applying the flow transformation. In contrast, many alternative generative modeling methods such as Variational autoencoder, variational autoencoder (VAE) and generative adversarial network do not explicitly represent the likelihood function. Method Let z_0 be a (possibly multivariate) random variable with distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generative Model
In statistical classification, two main approaches are called the generative approach and the discriminative approach. These compute classifiers by different approaches, differing in the degree of statistical modelling. Terminology is inconsistent, but three major types can be distinguished: # A generative model is a statistical model of the joint probability distribution P(X, Y) on a given observable variable ''X'' and target variable ''Y'';: "Generative classifiers learn a model of the joint probability, p(x, y), of the inputs ''x'' and the label ''y'', and make their predictions by using Bayes rules to calculate p(y\mid x), and then picking the most likely label ''y''. A generative model can be used to "generate" random instances ( outcomes) of an observation ''x''. # A discriminative model is a model of the conditional probability P(Y\mid X = x) of the target ''Y'', given an observation ''x''. It can be used to "discriminate" the value of the target variable ''Y'', given an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
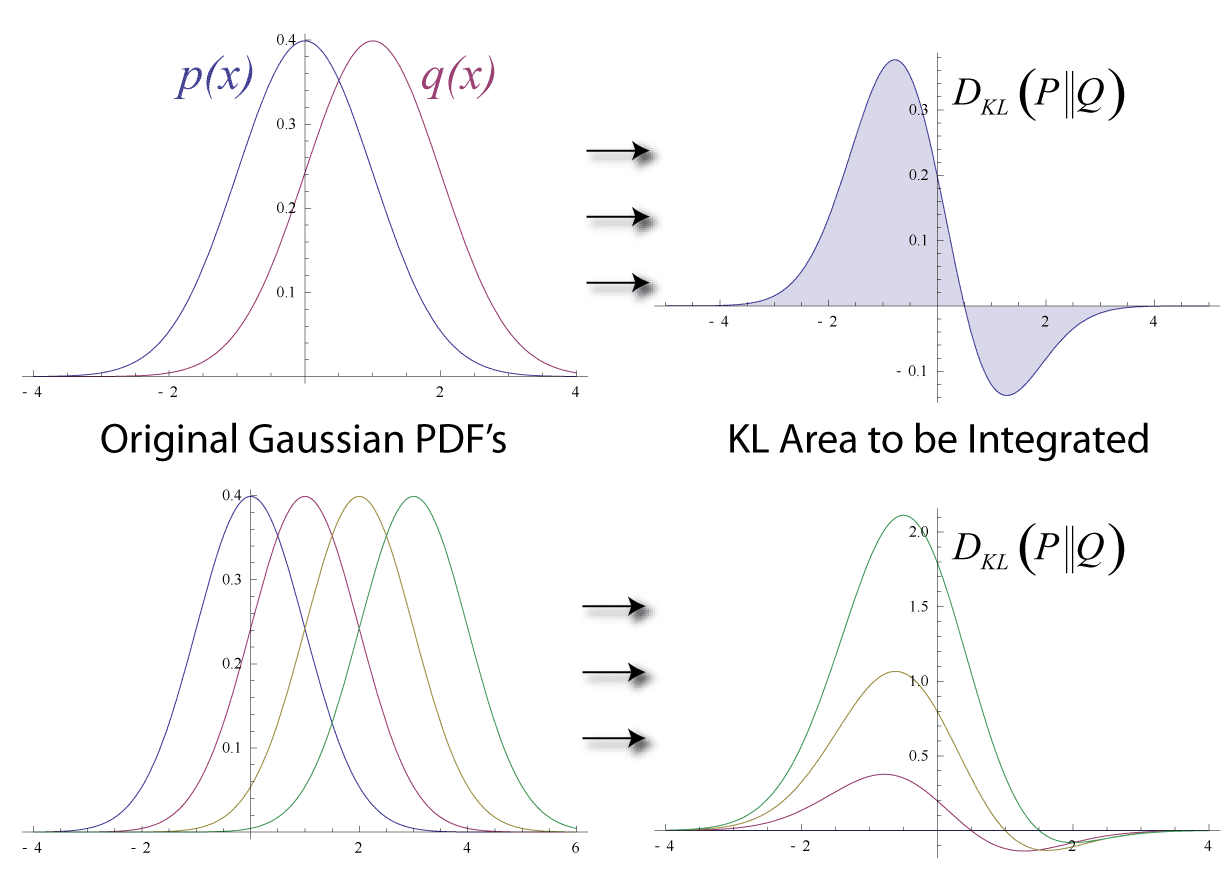
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Density
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a '' relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within a particular range o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Smooth Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Optimal Transport
In mathematics and economics, transportation theory or transport theory is a name given to the study of optimal transportation and allocation of resources. The problem was formalized by the French mathematician Gaspard Monge in 1781.G. Monge. ''Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année'', pages 666–704, 1781. In the 1920s A.N. Tolstoi was one of the first to study the transportation problem mathematically. In 1930, in the collection ''Transportation Planning Volume I'' for the National Commissariat of Transportation of the Soviet Union, he published a paper "Methods of Finding the Minimal Kilometrage in Cargo-transportation in space". Major advances were made in the field during World War II by the Soviet mathematician and economist Leonid Kantorovich.L. Kantorovich. ''On the translocation of masses.'' C.R. (Doklady) Acad. Sci. URSS (N.S.) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Universal Approximation Theorem
In the mathematical theory of artificial neural networks, universal approximation theorems are theorems of the following form: Given a family of neural networks, for each function f from a certain function space, there exists a sequence of neural networks \phi_1, \phi_2, \dots from the family, such that \phi_n \to f according to some criterion. That is, the family of neural networks is dense in the function space. The most popular version states that feedforward networks with non-polynomial activation functions are dense in the space of continuous functions between two Euclidean spaces, with respect to the compact convergence topology. Universal approximation theorems are existence theorems: They simply state that there ''exists'' such a sequence \phi_1, \phi_2, \dots \to f, and do not provide any way to actually find such a sequence. They also do not guarantee any method, such as backpropagation, might actually find such a sequence. Any method for searching the space of neural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Whitney Embedding Theorem
In mathematics, particularly in differential topology, there are two Whitney embedding theorems, named after Hassler Whitney: *The strong Whitney embedding theorem states that any smooth real - dimensional manifold (required also to be Hausdorff and second-countable) can be smoothly embedded in the real -space, if . This is the best linear bound on the smallest-dimensional Euclidean space that all -dimensional manifolds embed in, as the real projective spaces of dimension cannot be embedded into real -space if is a power of two (as can be seen from a characteristic class argument, also due to Whitney). *The weak Whitney embedding theorem states that any continuous function from an -dimensional manifold to an -dimensional manifold may be approximated by a smooth embedding provided . Whitney similarly proved that such a map could be approximated by an immersion provided . This last result is sometimes called the Whitney immersion theorem. About the proof Weak embedding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sphere Eversion
In differential topology, sphere eversion is a theoretical process of turning a sphere inside out in a three-dimensional space (the word ''wikt:eversion#English, eversion'' means "turning inside out"). It is possible to smoothly and continuously turn a sphere inside out in this way (allowing self-intersections of the sphere's surface) without cutting or tearing it or creating any Line (geometry), crease. This is surprising, both to non-mathematicians and to those who understand regular homotopy, and can be regarded as a veridical paradox; that is something that, while being true, on first glance seems false. More precisely, let :f\colon S^2\to \R^3 be the standard embedding; then there is a regular homotopy of immersion (mathematics), immersions :f_t\colon S^2\to \R^3 such that ''ƒ''0 = ''ƒ'' and ''ƒ''1 = −''ƒ''. History An existence proof for crease-free sphere eversion was first created by . It is difficult to visualize a particular example ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ambient Isotopy
In the mathematical subject of topology, an ambient isotopy, also called an ''h-isotopy'', is a kind of continuous distortion of an ambient space, for example a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the other without breaking it. Such a distortion is an example of an ambient isotopy. More precisely, let N and M be manifolds and g and h be embeddings of N in M. A continuous map :F:M \times ,1\rightarrow M is defined to be an ambient isotopy taking g to h if F_0 is the identity map, each map F_t is a homeomorphism from M to itself, and F_1 \circ g = h. This implies that the orientation must be preserved by ambient isotopies. For example, two knots that are mirror images of each other are, in general, not equivalent. See also * Isotopy * Regular homotopy *Regular isotopy References *M. A. Armstrong, ''Basic Topology'', Springer-Verlag Springer Science+Business M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Neural ODE
Neural differential equations are a class of models in machine learning that combine neural networks with the mathematical framework of differential equations. These models provide an alternative approach to neural network design, particularly for systems that evolve over time or through continuous transformations. The most common type, a neural ordinary differential equation (neural ODE), defines the evolution of a system's state using an ordinary differential equation whose dynamics are governed by a neural network: \frac=f_\theta(\mathbf(t), t).In this formulation, the neural network parameters ''θ'' determine how the state changes at each point in time. This approach contrasts with conventional neural networks, where information flows through discrete layers indexed by natural numbers. Neural ODEs instead use continuous layers indexed by positive real numbers, where the function h: \mathbb_ \to \mathbb represents the network's state at any given layer depth ''t''. Neural ODE ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rademacher Distribution
In probability theory and statistics, the Rademacher distribution (which is named after Hans Rademacher) is a discrete probability distribution where a random variate ''X'' has a 50% chance of being +1 and a 50% chance of being −1. A series (that is, a sum) of Rademacher distributed variables can be regarded as a simple symmetrical random walk where the step size is 1. Mathematical formulation The probability mass function of this distribution is : f(k) = \left\{\begin{matrix} 1/2 & \text{if }k=-1, \\ 1/2 & \text{if }k=+1, \\ 0 & \text{otherwise.}\end{matrix}\right. In terms of the Dirac delta function, as : f( k ) = \frac{ 1 }{ 2 } ( \delta (k - 1) + \delta (k + 1)). Bounds on sums of independent Rademacher variables There are various results in probability theory around analyzing the sum of i.i.d. Rademacher variables, including concentration inequalities such as Bernstein inequalities as well as anti-concentration inequalities like Tomaszewski's conjecture. Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |