|
Nonlocal Operator
In mathematics, a nonlocal operator is a mapping which maps functions on a topological space to functions, in such a way that the value of the output function at a given point cannot be determined solely from the values of the input function in any neighbourhood of any point. An example of a nonlocal operator is the Fourier transform. Formal definition Let X be a topological space, Y a set, F(X) a function space containing functions with domain X, and G(Y) a function space containing functions with domain Y. Two functions u and v in F(X) are called equivalent at x\in X if there exists a neighbourhood N of x such that u(x')=v(x') for all x'\in N. An operator A: F(X) \to G is said to be local if for every y\in Y there exists an x\in X such that Au(y) = Av(y) for all functions u and v in F(X) which are equivalent at x. A nonlocal operator is an operator which is not local. For a local operator it is possible (in principle) to compute the value Au(y) using only knowledge of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Surfaces
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below). The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However, the term is used for more general surfaces that may self-intersect or do not have constraints. For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum. Definitions Minimal surfaces can be defined in several equivalent ways in R3. The fact that they are equivalent serves to demonstrate how minimal surface theory lies at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Action At A Distance
In physics, action at a distance is the concept that an object can be affected without being physically touched (as in mechanical contact) by another object. That is, it is the non-local interaction of objects that are separated in space. Non-contact forces is action at a distance affecting specifically an object's motion. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant objects. For example, Coulomb's law and Newton's law of universal gravitation are such early theories. More generally, "action at a distance" describes the failure of early atomistic and mechanistic theories which sought to reduce all physical interaction to collision. The exploration and resolution of this problematic phenomenon led to significant developments in physics, from the concept of a field, to descriptions of quantum entanglement and the mediator particles of the Standard Model. Electric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlocal Lagrangian
In field theory, a nonlocal Lagrangian is a Lagrangian, a type of functional \mathcalphi(x) containing terms that are ''nonlocal'' in the fields \phi(x), i.e. not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (e.g. space-time). Examples of such nonlocal Lagrangians might be: * \mathcal = \frac\big(\partial_x \phi(x)\big)^2 - \fracm^2 \phi(x)^2 + \phi(x) \int \frac \,d^ny. * \mathcal = -\frac\mathcal_\left(1 + \frac\right)\mathcal^. * S = \int dt \,d^dx \left psi^*\left(i\hbar \frac + \mu\right)\psi - \frac\nabla \psi^*\cdot \nabla \psi\right- \frac\int dt \,d^dx \,d^dy \, V(\mathbf - \mathbf) \psi^*(\mathbf) \psi(\mathbf) \psi^*(\mathbf) \psi(\mathbf). * The Wess–Zumino–Witten action. Actions obtained from nonlocal Lagrangians are called ''nonlocal actions''. The actions appearing in the fundamental theories of physics, such as the Standard Model, are local actions; nonlocal actions play a par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) ''endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
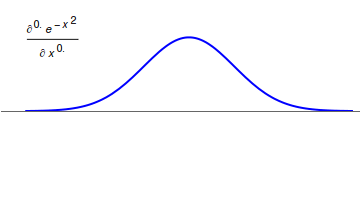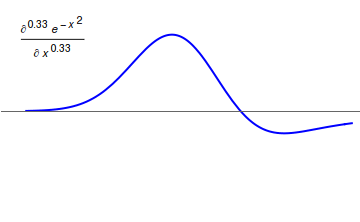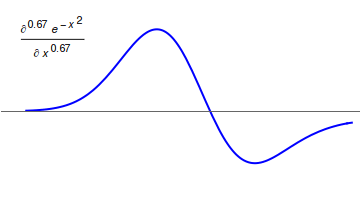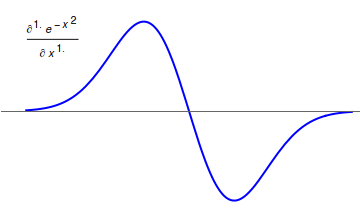
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel (image Processing)
In image processing, a kernel, convolution matrix, or mask is a small matrix used for blurring, sharpening, embossing, edge detection, and more. This is accomplished by doing a convolution between the kernel and an image. Details The general expression of a convolution is g(x,y)= \omega *f(x,y)=\sum_^a, where g(x,y) is the filtered image, f(x,y) is the original image, \omega is the filter kernel. Every element of the filter kernel is considered by -a \leq dx \leq a and -b \leq dy \leq b. Depending on the element values, a kernel can cause a wide range of effects. . The above are just a few examples of effects achievable by convolving kernels and images. Origin The origin is the position of the kernel which is above (conceptually) the current output pixel. This could be outside of the actual kernel, though usually it corresponds to one of the kernel elements. For a symmetric kernel, the origin is usually the center element. Convolution Convolution is the pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Motion Blur
Motion blur is the apparent streaking of moving objects in a photograph or a sequence of frames, such as a film or animation. It results when the image being recorded changes during the recording of a single exposure, due to rapid movement or long exposure. Usages / Effects of motion blur Photography When a camera creates an image, that image does not represent a single instant of time. Because of technological constraints or artistic requirements, the image may represent the scene over a period of time. Most often this exposure time is brief enough that the image captured by the camera appears to capture an instantaneous moment, but this is not always so, and a fast moving object or a longer exposure time may result in blurring artifacts which make this apparent. As objects in a scene move, an image of that scene must represent an integration of all positions of those objects, as well as the camera's viewpoint, over the period of exposure determined by the shutter speed. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Blur
In image processing, a Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function (named after mathematician and scientist Carl Friedrich Gauss). It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales—see scale space representation and scale space implementation. Mathematics Mathematically, applying a Gaussian blur to an image is the same as convolving the image with a Gaussian function. This is also known as a two-dimensional Weierstrass transform. By contrast, convolving by a circ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-local Means
Non-local means is an algorithm in image processing for image denoising. Unlike "local mean" filters, which take the mean value of a group of pixels surrounding a target pixel to smooth the image, non-local means filtering takes a mean of all pixels in the image, weighted by how similar these pixels are to the target pixel. This results in much greater post-filtering clarity, and less loss of detail in the image compared with local mean algorithms. If compared with other well-known denoising techniques, non-local means adds "method noise" (i.e. error in the denoising process) which looks more like white noise, which is desirable because it is typically less disturbing in the denoised product. Recently non-local means has been extended to other image processing applications such as deinterlacing, view interpolation, and depth maps regularization. Definition Suppose \Omega is the area of an image, and p and q are two points within the image. Then, the algorithm is: :u(p) = \int_\Om ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |