|
Nicomachus
Nicomachus of Gerasa ( grc-gre, Νικόμαχος; c. 60 – c. 120 AD) was an important ancient mathematician and music theorist, best known for his works ''Introduction to Arithmetic'' and ''Manual of Harmonics'' in Greek. He was born in Gerasa, in the Roman province of Syria (now Jerash, Jordan). He was a Neopythagorean, who wrote about the mystical properties of numbers.Eric Temple Bell (1940), ''The development of mathematics'', page 83.Frank J. Swetz (2013), ''The European Mathematical Awakening'', page 17, Courier Life Little is known about the life of Nicomachus except that he was a Pythagorean who came from Gerasa.} Historians consider him a Neopythagorean based on his tendency to view numbers as having mystical properties. The age in which he lived (c. 100 AD) is only known because he mentions Thrasyllus in his ''Manual of Harmonics'', and because his ''Introduction to Arithmetic'' was apparently translated into Latin in the mid 2nd century by Apuleius.Henrietta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nicomachus Theorem 3D
Nicomachus of Gerasa ( grc-gre, Νικόμαχος; c. 60 – c. 120 AD) was an important ancient mathematician and music theorist, best known for his works ''Introduction to Arithmetic'' and ''Manual of Harmonics'' in Greek. He was born in Gerasa, in the Roman province of Syria (now Jerash, Jordan). He was a Neopythagorean, who wrote about the mystical properties of numbers.Eric Temple Bell (1940), ''The development of mathematics'', page 83.Frank J. Swetz (2013), ''The European Mathematical Awakening'', page 17, Courier Life Little is known about the life of Nicomachus except that he was a Pythagorean who came from Gerasa.} Historians consider him a Neopythagorean based on his tendency to view numbers as having mystical properties. The age in which he lived (c. 100 AD) is only known because he mentions Thrasyllus in his ''Manual of Harmonics'', and because his ''Introduction to Arithmetic'' was apparently translated into Latin in the mid 2nd century by Apuleius.Henrietta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Introduction To Arithmetic
The book ''Introduction to Arithmetic'' ( grc-gre, Ἀριθμητικὴ εἰσαγωγή, ''Arithmetike eisagoge'') is the only extant work on mathematics by Nicomachus (60–120 AD). Summary The work contains both philosophical prose and basic mathematical ideas. Nicomachus refers to Plato quite often, and writes that philosophy can only be possible if one knows enough about mathematics. Nicomachus also describes how natural numbers and basic mathematical ideas are eternal and unchanging, and in an abstract realm. It consists of two books, twenty-three and twenty-nine chapters, respectively. Although he was preceded by the Babylonians and the Chinese, Nicomachus provided one of the earliest Greco-Roman multiplication tables, whereas the oldest extant Greek multiplication table is found on a wax tablet dated to the 1st century AD (now found in the British Museum). Influence The ''Introduction to Arithmetic'' of Nicomachus was a standard textbook in Neoplatonic schools an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagoreanism
Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the Ancient Greece, ancient Greek colony of Crotone, Kroton, in modern Calabria (Italy). Early Pythagorean communities spread throughout Magna Graecia. Pythagoras' death and disputes about his teachings led to the development of two philosophical traditions within Pythagoreanism. The ''akousmatikoi'' were superseded in the 4th century BC as a significant mendicant school of philosophy by the Cynicism (philosophy), Cynics. The ''mathēmatikoi'' philosophers were absorbed into the Platonic Academy, Platonic school in the 4th century BC. Following political instability in Magna Graecia, some Pythagorean philosophers fled to mainland Greece while others regrouped in Rhegium. By about 400 BC the majority of Pythagorean philosophers had left Italy. Pythagorean ideas exercised a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boethius
Anicius Manlius Severinus Boethius, commonly known as Boethius (; Latin: ''Boetius''; 480 – 524 AD), was a Roman senator, consul, ''magister officiorum'', historian, and philosopher of the Early Middle Ages. He was a central figure in the translation of the Greek classics into Latin, a precursor to the Scholastic movement, and, along with Cassiodorus, one of the two leading Christian scholars of the 6th century. The local cult of Boethius in the Diocese of Pavia was sanctioned by the Sacred Congregation of Rites in 1883, confirming the diocese's custom of honouring him on the 23 October. Boethius was born in Rome a few years after the collapse of the Western Roman Empire. A member of the Anicii family, he was orphaned following the family's sudden decline and was raised by Quintus Aurelius Memmius Symmachus, a later consul. After mastering both Latin and Greek in his youth, Boethius rose to prominence as a statesman during the Ostrogothic Kingdom: becoming a senator by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Numbers
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number. The sum of divisors of a number, excluding the number itself, is called its aliquot sum, so a perfect number is one that is equal to its aliquot sum. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors including itself; in symbols, \sigma_1(n)=2n where \sigma_1 is the sum-of-divisors function. For instance, 28 is perfect as 1 + 2 + 4 + 7 + 14 = 28. This definition is ancient, appearing as early as Euclid's ''Elements'' (VII.22) where it is called (''perfect'', ''ideal'', or ''complete number''). Euclid also proved a formation rule (IX.36) whereby q(q+1)/2 is an even perfect number whenever q is a prime of the form 2^p-1 for positive integer p—what is now called a Mersenne prime. Two millennia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
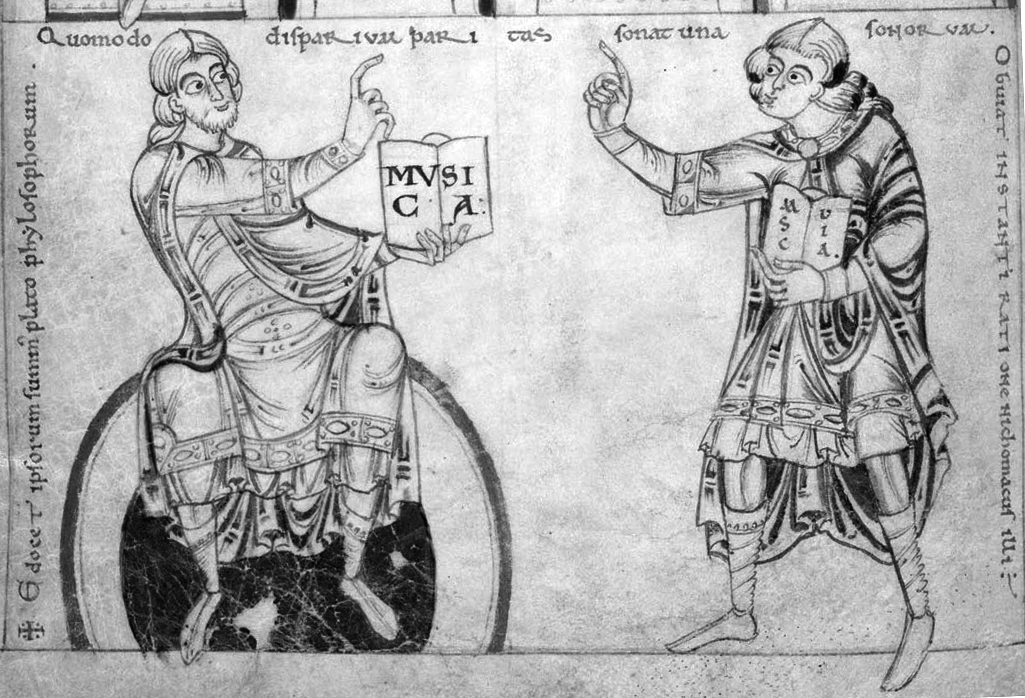
Music Theorist
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (key signatures, time signatures, and rhythmic notation); the second is learning scholars' views on music from antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built." Music theory is frequently concerned with describing how musicians and composers make music, including tuning systems and composition methods among other topics. Because of the ever-expanding conception of what constitutes music, a more inclusive definition could be the consideration of any sonic phenomena, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerasa
Jerash ( ar, جرش ''Ǧaraš''; grc, Γέρασα ''Gérasa'') is a city in northern Jordan. The city is the administrative center of the Jerash Governorate, and has a population of 50,745 as of 2015. It is located north of the capital city Amman. The earliest evidence of settlement in Jerash is in a Neolithic site known as Tal Abu Sowan, where rare human remains dating to around 7500 BC were uncovered. Jerash flourished during the Greek, Hellenistic, Roman, and Byzantine periods until the mid-eighth century CE, when the 749 Galilee earthquake destroyed large parts of it, while subsequent earthquakes contributed to additional destruction. However, in the year 1120, Zahir ad-Din Toghtekin, atabeg of Damascus ordered a garrison of forty men to build up a fort in an unknown site of the ruins of the ancient city, likely the highest spot of the city walls in the north-eastern hills. It was captured in 1121 by Baldwin II, King of Jerusalem, and utterly destroyed. Then, the Crusad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerash
Jerash ( ar, جرش ''Ǧaraš''; grc, Γέρασα ''Gérasa'') is a city in northern Jordan. The city is the administrative center of the Jerash Governorate, and has a population of 50,745 as of 2015. It is located north of the capital city Amman. The earliest evidence of settlement in Jerash is in a Neolithic site known as Tal Abu Sowan, where rare human remains dating to around 7500 BC were uncovered. Jerash flourished during the Greek, Hellenistic, Roman, and Byzantine periods until the mid-eighth century CE, when the 749 Galilee earthquake destroyed large parts of it, while subsequent earthquakes contributed to additional destruction. However, in the year 1120, Zahir ad-Din Toghtekin, atabeg of Damascus ordered a garrison of forty men to build up a fort in an unknown site of the ruins of the ancient city, likely the highest spot of the city walls in the north-eastern hills. It was captured in 1121 by Baldwin II, King of Jerusalem, and utterly destroyed. Then, the Crusad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neopythagorean
Neopythagoreanism (or neo-Pythagoreanism) was a school of Hellenistic philosophy which revived Pythagorean doctrines. Neopythagoreanism was influenced by middle Platonism and in turn influenced Neoplatonism. It originated in the 1st century BC and flourished during the 1st and 2nd centuries AD. The ''Encyclopædia Britannica'' Eleventh Edition describes Neopythagoreanism as "a link in the chain between the old and the new" within Hellenistic philosophy. Central to Neopythagorean thought was the concept of a soul and its inherent desire for a ''unio mystica'' with the divine. The word ''Neopythagoreanism'' is a modern (19th century) term, coined as a parallel of "Neoplatonism". History In the 1st century BC Cicero's friend Nigidius Figulus made an attempt to revive Pythagorean doctrines, but the most important members of the school were Apollonius of Tyana and Moderatus of Gades in the 1st century AD. Other important Neopythagoreans include the mathematician Nicomachus of Gerasa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Numbers
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neopythagoreanism
Neopythagoreanism (or neo-Pythagoreanism) was a school of Hellenistic philosophy which revived Pythagorean doctrines. Neopythagoreanism was influenced by middle Platonism and in turn influenced Neoplatonism. It originated in the 1st century BC and flourished during the 1st and 2nd centuries AD. The ''Encyclopædia Britannica'' Eleventh Edition describes Neopythagoreanism as "a link in the chain between the old and the new" within Hellenistic philosophy. Central to Neopythagorean thought was the concept of a soul and its inherent desire for a ''unio mystica'' with the divine. The word ''Neopythagoreanism'' is a modern (19th century) term, coined as a parallel of "Neoplatonism". History In the 1st century BC Cicero's friend Nigidius Figulus made an attempt to revive Pythagorean doctrines, but the most important members of the school were Apollonius of Tyana and Moderatus of Gades in the 1st century AD. Other important Neopythagoreans include the mathematician Nicomachus of Gera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |