|
Nakagami Distribution
The Nakagami distribution or the Nakagami-''m'' distribution is a probability distribution related to the gamma distribution. The family of Nakagami distributions has two parameters: a shape parameter m\geq 1/2 and a second parameter controlling spread \Omega>0. Characterization Its probability density function (pdf) is : f(x;\,m,\Omega) = \fracx^\exp\left(-\fracx^2\right), \forall x\geq 0. where (m\geq 1/2,\text\Omega>0) Its cumulative distribution function is : F(x;\,m,\Omega) = P\left(m, \fracx^2\right) where ''P'' is the regularized (lower) incomplete gamma function. Parametrization The parameters m and \Omega are : m = \frac , and : \Omega = \operatorname \left ^2 \right Parameter estimation An alternative way of fitting the distribution is to re-parametrize \Omega and ''m'' as ''σ'' = Ω/''m'' and ''m''. Given independent observations X_1=x_1,\ldots,X_n=x_n from the Nakagami distribution, the likelihood function is : L( \s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nakagami Pdf
Nakagami (written: 中上) is a Japanese surname. Notable people with the surname include: *, Japanese therapist * (1946–1992), Japanese writer, critic and poet * (born 1992), Japanese motorcycle racer See also * Nakagami District, Okinawa * Nakagami distribution The Nakagami distribution or the Nakagami-''m'' distribution is a probability distribution related to the gamma distribution. The family of Nakagami distributions has two parameters: a shape parameter m\geq 1/2 and a second parameter controlling ..., a statistical distribution {{surname, Nakagami Japanese-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Normal
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Normal Table
A standard normal table, also called the unit normal table or Z table, is a mathematical table for the values of Φ, which are the values of the cumulative distribution function of the normal distribution. It is used to find the probability that a statistic is observed below, above, or between values on the standard normal distribution, and by extension, any normal distribution. Since probability tables cannot be printed for every normal distribution, as there are an infinite variety of normal distributions, it is common practice to convert a normal to a standard normal and then use the standard normal table to find probabilities. Normal and standard normal distribution Normal distributions are symmetrical, bell-shaped distributions that are useful in describing real-world data. The ''standard'' normal distribution, represented by the letter Z, is the normal distribution having a mean of 0 and a standard deviation of 1. Conversion If ''X'' is a random variable from a normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio Normal Distribution
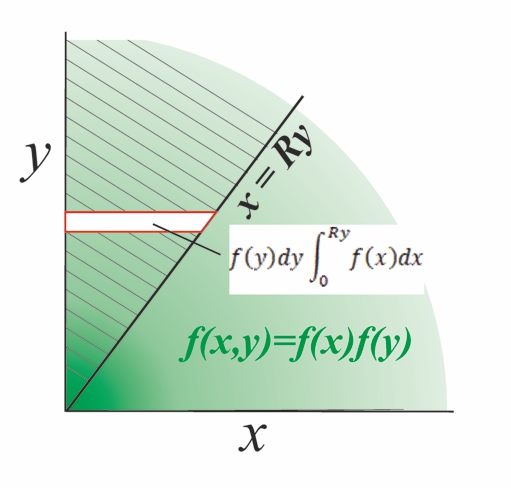
A ratio distribution (also known as a quotient distribution) is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two (usually independent) random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the ratio ''Z'' = ''X''/''Y'' is a ''ratio distribution''. An example is the Cauchy distribution (also called the ''normal ratio distribution''), which comes about as the ratio of two normally distributed variables with zero mean. Two other distributions often used in test-statistics are also ratio distributions: the ''t''-distribution arises from a Gaussian random variable divided by an independent chi-distributed random variable, while the ''F''-distribution originates from the ratio of two independent chi-squared distributed random variables. More general ratio distributions have been considered in the literature. Often the ratio distributions are heavy- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Normal Distribution
In probability theory and statistics, an inverse distribution is the distribution of the reciprocal of a random variable. Inverse distributions arise in particular in the Bayesian context of prior distributions and posterior distributions for scale parameters. In the algebra of random variables, inverse distributions are special cases of the class of ratio distributions, in which the numerator random variable has a degenerate distribution. Relation to original distribution In general, given the probability distribution of a random variable ''X'' with strictly positive support, it is possible to find the distribution of the reciprocal, ''Y'' = 1 / ''X''. If the distribution of ''X'' is continuous with density function ''f''(''x'') and cumulative distribution function ''F''(''x''), then the cumulative distribution function, ''G''(''y''), of the reciprocal is found by noting that : G(y) = \Pr(Y \leq y) = \Pr\left(X \geq \frac\right) = 1-\Pr\left(X<\frac\right) = 1 - F\left( \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normally Distributed And Uncorrelated Does Not Imply Independent
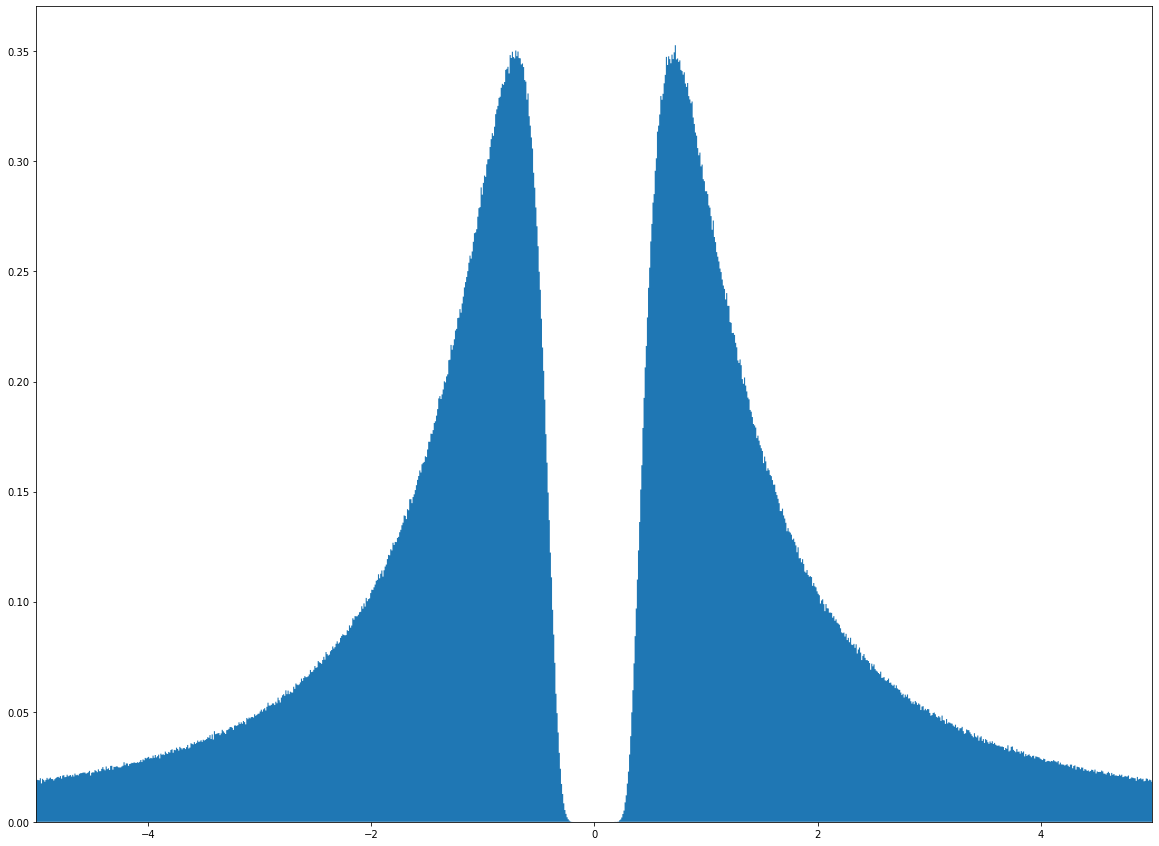
In probability theory, although simple examples illustrate that linear uncorrelatedness of two random variables does not in general imply their independence, it is sometimes mistakenly thought that it does imply that when the two random variables are normally distributed. This article demonstrates that assumption of normal distributions does not have that consequence, although the multivariate normal distribution, including the bivariate normal distribution, does. To say that the pair (X,Y) of random variables has a bivariate normal distribution means that every linear combination aX+bY of X and Y for constant (i.e. not random) coefficients a and b (not both equal to zero) has a univariate normal distribution. In that case, if X and Y are uncorrelated then they are independent. However, it is possible for two random variables X and Y to be so distributed jointly that each one alone is marginally normally distributed, and they are uncorrelated, but they are not independent; exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |