|
Noncommutative Signal-flow Graph
In automata theory and control theory, branches of mathematics, theoretical computer science and systems engineering, a noncommutative signal-flow graph is a tool for modeling interconnected systems and state machines by mapping the edges of a directed graph to a ring (mathematics), ring or semiring. A single edge weight might represent an array of impulse responses of a complex system (see figure to the right), or a character from an Alphabet (computer science), alphabet picked off the Finite state transducer, input tape of a finite automaton, while the graph might represent the flow of information or state transitions. As diverse as these applications are, they share much of the same underlying theory. Definition Consider ''n'' equations involving ''n''+1 variables . :x_i = \sum_^n a_x_j, \;\;\; 1\leq i \leq n, with ''a''ij elements in a ring or semiring ''R''. The free variable ''x''0 corresponds to a source vertex ''v''0, thus having no defining equation. Each equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
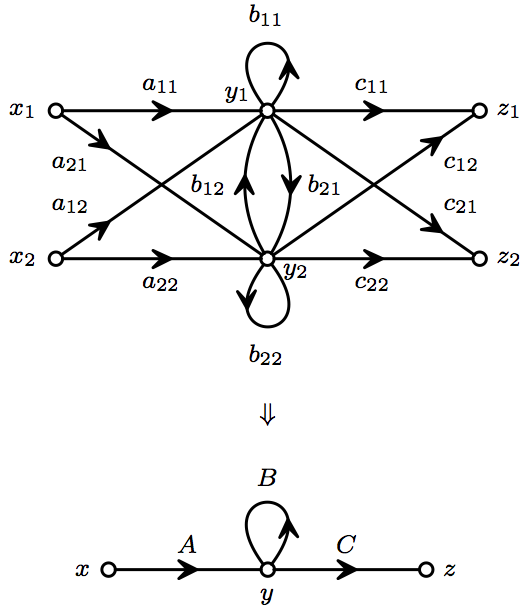
Matrix Signal-Flow Graph
Matrix most commonly refers to: * The Matrix (franchise), ''The Matrix'' (franchise), an American media franchise ** ''The Matrix'', a 1999 science-fiction action film ** "The Matrix", a fictional setting, a virtual reality environment, within The Matrix (franchise), ''The Matrix'' (franchise) * Matrix (mathematics), a rectangular array of numbers, symbols or expressions Matrix (or its plural form matrices) may also refer to: Science and mathematics * Matrix (mathematics), algebraic structure, extension of vector into 2 dimensions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Arts and entertainment Fiction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FRL BRL Example
FRL can refer to: * Fairlie railway station, in Scotland * Film Reference Library, a Canadian film archive * Fire Research Laboratory, part of the United States Bureau of Alcohol, Tobacco, Firearms and Explosives * '' Fish Rap Live!'', a publication at the University of California, Santa Cruz * Flight Refuelling Ltd, now Cobham plc, a British manufacturer * Florida Rookie League, now the Gulf Coast League, an American Minor League Baseball league * Forlì Airport, in Italy * Frame representation language * Freedom Airlines, a defunct American airline * French Radio London, a French-language internet radio station based in London * Friesland, a province of the Netherlands ** .frl, the Internet top-level domain for Friesland * Fundació Ramon Llull (Ramon Llull Foundation) a Catalan cultural organization * ''Furnace Room Lullaby'', an album by Neko Case & Her Boyfriends * Freedom of Russia Legion, Russians fighting for Ukraine during the 2022 Russian invasion of Ukraine On 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-flow Graph
A signal-flow graph or signal-flowgraph (SFG), invented by Claude Shannon, but often called a Mason graph after Samuel Jefferson Mason who coined the term, is a specialized flow graph, a directed graph in which nodes represent system variables, and branches (edges, arcs, or arrows) represent functional connections between pairs of nodes. Thus, signal-flow graph theory builds on that of directed graphs (also called digraphs), which includes as well that of oriented graphs. This mathematical theory of digraphs exists, of course, quite apart from its applications. i SFGs are most commonly used to represent signal flow in a physical system and its controller(s), forming a cyber-physical system. Among their other uses are the representation of signal flow in various electronic networks and amplifiers, digital filters, state-variable filters and some other types of analog filters. In nearly all literature, a signal-flow graph is associated with a set of linear equations. Histo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules. The alphabet of a formal language consists of symbols, letters, or tokens that concatenate into strings of the language. Each string concatenated from symbols of this alphabet is called a word, and the words that belong to a particular formal language are sometimes called ''well-formed words'' or ''well-formed formulas''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar, which consists of its formation rules. In computer science, formal languages are used among others as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages in which the words of the language represent concepts that are associated with particular meanings or semantics. In computational complexity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singleton (mathematics)
In mathematics, a singleton, also known as a unit set or one-point set, is a set with exactly one element. For example, the set \ is a singleton whose single element is 0. Properties Within the framework of Zermelo–Fraenkel set theory, the axiom of regularity guarantees that no set is an element of itself. This implies that a singleton is necessarily distinct from the element it contains, thus 1 and are not the same thing, and the empty set is distinct from the set containing only the empty set. A set such as \ is a singleton as it contains a single element (which itself is a set, however, not a singleton). A set is a singleton if and only if its cardinality is . In von Neumann's set-theoretic construction of the natural numbers, the number 1 is ''defined'' as the singleton \. In axiomatic set theory, the existence of singletons is a consequence of the axiom of pairing: for any set ''A'', the axiom applied to ''A'' and ''A'' asserts the existence of \, which is the same a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Expressions
A regular expression (shortened as regex or regexp; sometimes referred to as rational expression) is a sequence of characters that specifies a search pattern in text. Usually such patterns are used by string-searching algorithms for "find" or "find and replace" operations on strings, or for input validation. Regular expression techniques are developed in theoretical computer science and formal language theory. The concept of regular expressions began in the 1950s, when the American mathematician Stephen Cole Kleene formalized the concept of a regular language. They came into common use with Unix text-processing utilities. Different syntaxes for writing regular expressions have existed since the 1980s, one being the POSIX standard and another, widely used, being the Perl syntax. Regular expressions are used in search engines, in search and replace dialogs of word processors and text editors, in text processing utilities such as sed and AWK, and in lexical analysis. Most gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empty Word
In formal language theory, the empty string, or empty word, is the unique string of length zero. Formal theory Formally, a string is a finite, ordered sequence of characters such as letters, digits or spaces. The empty string is the special case where the sequence has length zero, so there are no symbols in the string. There is only one empty string, because two strings are only different if they have different lengths or a different sequence of symbols. In formal treatments, the empty string is denoted with ε or sometimes Λ or λ. The empty string should not be confused with the empty language ∅, which is a formal language (i.e. a set of strings) that contains no strings, not even the empty string. The empty string has several properties: * , ε, = 0. Its string length is zero. * ε ⋅ s = s ⋅ ε = s. The empty string is the identity element of the concatenation operation. The set of all strings forms a free monoid with respect to ⋅ and ε. * εR = ε. Reversal of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene Closure
In mathematical logic and computer science, the Kleene star (or Kleene operator or Kleene closure) is a unary operation, either on sets of strings or on sets of symbols or characters. In mathematics, it is more commonly known as the free monoid construction. The application of the Kleene star to a set V is written as ''V^*''. It is widely used for regular expressions, which is the context in which it was introduced by Stephen Kleene to characterize certain automata, where it means "zero or more repetitions". # If V is a set of strings, then ''V^*'' is defined as the smallest superset of V that contains the empty string \varepsilon and is closed under the string concatenation operation. # If V is a set of symbols or characters, then ''V^*'' is the set of all strings over symbols in V, including the empty string \varepsilon. The set ''V^*'' can also be described as the set containing the empty string and all finite-length strings that can be generated by concatenating arbitrary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Union
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other. A refers to a union of zero (0) sets and it is by definition equal to the empty set. For explanation of the symbols used in this article, refer to the table of mathematical symbols. Union of two sets The union of two sets ''A'' and ''B'' is the set of elements which are in ''A'', in ''B'', or in both ''A'' and ''B''. In set-builder notation, :A \cup B = \. For example, if ''A'' = and ''B'' = then ''A'' ∪ ''B'' = . A more elaborate example (involving two infinite sets) is: : ''A'' = : ''B'' = : A \cup B = \ As another example, the number 9 is ''not'' contained in the union of the set of prime number A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Monoid
In abstract algebra, the free monoid on a set is the monoid whose elements are all the finite sequences (or strings) of zero or more elements from that set, with string concatenation as the monoid operation and with the unique sequence of zero elements, often called the empty string and denoted by ε or λ, as the identity element. The free monoid on a set ''A'' is usually denoted ''A''∗. The free semigroup on ''A'' is the subsemigroup of ''A''∗ containing all elements except the empty string. It is usually denoted ''A''+./ref> More generally, an abstract monoid (or semigroup) ''S'' is described as free if it is isomorphic to the free monoid (or semigroup) on some set. As the name implies, free monoids and semigroups are those objects which satisfy the usual universal property defining free objects, in the respective categories of monoids and semigroups. It follows that every monoid (or semigroup) arises as a homomorphic image of a free monoid (or semigroup). The study ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automaton
An automaton (; plural: automata or automatons) is a relatively self-operating machine, or control mechanism designed to automatically follow a sequence of operations, or respond to predetermined instructions.Automaton – Definition and More from the Free Merriam-Webster Dictionary http://www.merriam-webster.com/dictionary/automaton Some automata, such as Jacquemart (bellstriker), bellstrikers in mechanical clocks, are designed to give the illusion to the casual observer that they are operating under their own power. Since long ago, the term is commonly associated with automated puppets that resemble moving humans or animals, built to impress and/or to entertain people. Animatronics are a modern type of automata with electronics, often used for the portrayal of characters in films and in theme park attractions. Etymology The word "automaton" is the latinization of the Ancient Greek , , (neuter) "acting of one's own will". This word was first used by Homer to describe an auto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite-state Machine
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of '' states'' at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types— deterministic finite-state machines and non-deterministic finite-state machines. A deterministic finite-state machine can be constructed equivalent to any non-deterministic one. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are vending machines, which dispense p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
