|
Newton's Law Of Cooling
In the study of heat transfer, Newton's law of cooling is a physical law which states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its environment. The law is frequently qualified to include the condition that the temperature difference is small and the nature of heat transfer mechanism remains the same. As such, it is equivalent to a statement that the heat transfer coefficient, which mediates between heat losses and temperature differences, is a constant. In heat conduction, Newton's law is generally followed as a consequence of Fourier's law. The thermal conductivity of most materials is only weakly dependent on temperature, so the constant heat transfer coefficient condition is generally met. In convective heat transfer, Newton's Law is followed for forced air or pumped fluid cooling, where the properties of the fluid do not vary strongly with temperature, but it is only approximately true for b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pierre Louis Dulong
Pierre Louis Dulong FRS FRSE (; ; 12 February 1785 – 19 July 1838) was a French physicist and chemist. He is remembered today largely for the law of Dulong and Petit, although he was much-lauded by his contemporaries for his studies into the elasticity of steam, conduction of heat, and specific heats of gases. He worked most extensively on the specific heat capacity and the expansion and refractive indices of gases. He collaborated the co-discoverer of the Dulong–Petit law. Early life and education Dulong was born in Rouen, France. An only child, he was orphaned at the age of 4, he was brought up by his aunt in Auxerre. He gained his secondary education in Auxerre and the Lycée Pierre Corneille in Rouen before entering the École polytechnique, Paris in 1801, only for his studies to be impeded by poor health. He began studying medicine, but gave this up, possibly because of a lack of financial means, to concentrate on science, working under the direction of Louis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics (more specifically thermodynamics), the heat equation is a parabolic partial differential equation. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. Since then, the heat equation and its variants have been found to be fundamental in many parts of both pure and applied mathematics. Definition Given an open subset of and a subinterval of , one says that a function is a solution of the heat equation if : \frac = \frac + \cdots + \frac, where denotes a general point of the domain. It is typical to refer to as time and as spatial variables, even in abstract contexts where these phrases fail to have their intuitive meaning. The collection of spatial variables is often referred to simply as . For any given value of , the right-hand side of the equation is the Laplace operator, Laplacian of the function . As such, the heat equation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Wiley & Sons
John Wiley & Sons, Inc., commonly known as Wiley (), is an American Multinational corporation, multinational Publishing, publishing company that focuses on academic publishing and instructional materials. The company was founded in 1807 and produces books, Academic journal, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, Technology, technical, and engineering subject areas, abandoning its literary interests. Wiley's son Joh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lumped-capacitance Model
The lumped-element model (also called lumped-parameter model, or lumped-component model) is a simplified representation of a physical system or circuit that assumes all components are concentrated at a single point and their behavior can be described by idealized mathematical models. The lumped-element model simplifies the system or circuit behavior description into a topology. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This is in contrast to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities. The simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters. Electrical systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Length
In physics, a characteristic length is an important dimension that defines the scale of a physical system. Often, such a length is used as an input to a formula in order to predict some characteristics of the system, and it is usually required by the construction of a dimensionless quantity, in the general framework of dimensional analysis and in particular applications such as fluid mechanics. In computational mechanics, a characteristic length is defined to force localization of a stress softening constitutive equation. The length is associated with an integration point. For 2D analysis, it is calculated by taking the square root of the area. For 3D analysis, it is calculated by taking the cubic root of the volume associated to the integration point. Examples A characteristic length is usually the volume of a system divided by its surface: L_c = \frac For example, it is used to calculate flow through circular and non-circular tubes in order to examine flow conditions (i.e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Layer
In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a Boundary (thermodynamic), bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a No-slip condition, no-slip boundary condition (zero velocity at the wall). The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer. The air next to a human is heated, resulting in gravity-induced convective airflow, which results in both a velocity and thermal boundary layer. A breeze disrupts the boundary layer, and hair and clothing protect it, making the human feel cooler or warmer. On an aircraft wing, the velocity boundary layer is the part of the flow close to the wing, where viscosity, viscous forces distort the surrounding non-viscous flow. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
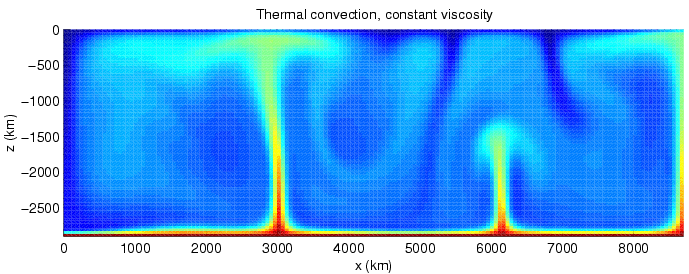
Turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to laminar flow, which occurs when a fluid flows in parallel layers with no disruption between those layers. Turbulence is commonly observed in everyday phenomena such as surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason, turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices appear of many sizes which interact with each other, consequently drag due to friction effects increases. The onset of turbulence can be predicted by the dimensionless Reynolds number, the ratio of kinetic energy to viscous damping ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watt
The watt (symbol: W) is the unit of Power (physics), power or radiant flux in the International System of Units (SI), equal to 1 joule per second or 1 kg⋅m2⋅s−3. It is used to quantification (science), quantify the rate of Work (physics), energy transfer. The watt is named in honor of James Watt (1736–1819), an 18th-century Scottish people, Scottish inventor, mechanical engineer, and chemist who improved the Newcomen engine with his own Watt steam engine, steam engine in 1776, which became fundamental for the Industrial Revolution. Overview When an object's velocity is held constant at one meter per second against a constant opposing force of one Newton (unit), newton, the rate at which Work (physics), work is done is one watt. \mathrm. In terms of electromagnetism, one watt is the rate at which electrical work is performed when a current of one ampere (A) flows across an electrical potential difference of one volt (V), meaning the watt is equivalent to the vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
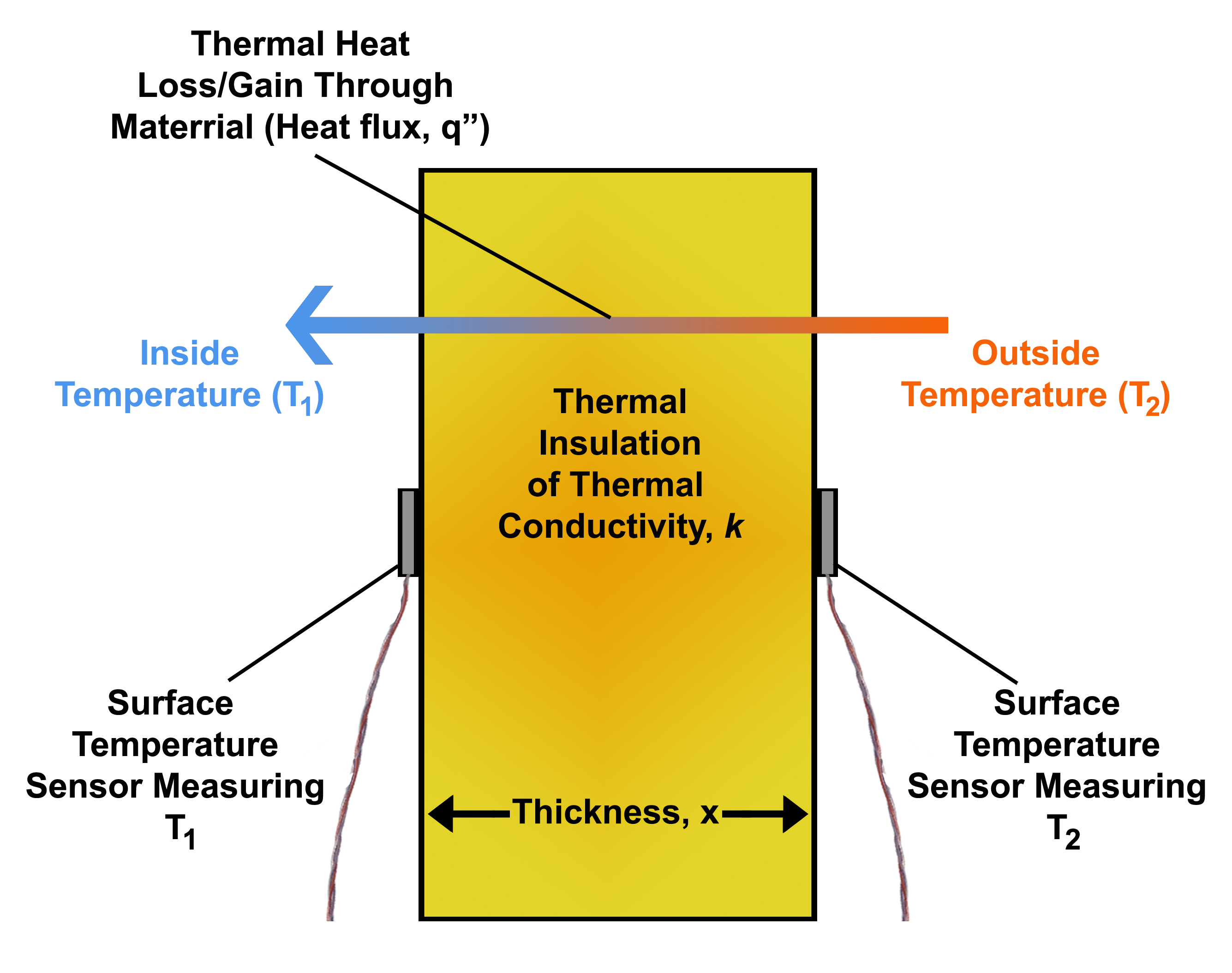
Heat Flux
In physics and engineering, heat flux or thermal flux, sometimes also referred to as heat flux density, heat-flow density or heat-flow rate intensity, is a flow of energy per unit area per unit time (physics), time. Its SI units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a Vector (geometric), vector quantity. To define the heat flux at a certain point in space, one takes the Limiting case (mathematics), limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''Mass flux, mass'' or Transport phenomena, ''momentum'' flux. Heat conduction#Fourier's law, Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by thermal conduction, conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan–Boltzmann Law
The Stefan–Boltzmann law, also known as ''Stefan's law'', describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically. For an ideal absorber/emitter or black body, the Stefan–Boltzmann law states that the total energy radiated per unit area, surface area per unit time (also known as the ''radiant exitance'') is directly Proportionality (mathematics), proportional to the fourth power of the black body's temperature, : M^ = \sigma\, T^. The constant of proportionality, \sigma, is called the Stefan–Boltzmann constant. It has the value In the general case, the Stefan–Boltzmann law for radiant exitance takes the form: M = \varepsilon\, M^ = \varepsilon\,\sigma\, T^4 , where \varepsilon is the emissivity of the surface emitting the radiation. The emissivity is generally between zero and one. An emiss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |