|
N-ary Associativity
In algebra, ''n''-ary associativity is a generalization of the associative law In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement f ... to ''n''-ary operations. Ternary associativity is : (''abc'')''de'' = ''a''(''bcd'')''e'' = ''ab''(''cde''), i.e. the string ''abcde'' with any three adjacent elements bracketed. ''n''-ary associativity is a string of length ''n'' + (''n'' − 1) with any ''n'' adjacent elements bracketed.. References Properties of binary operations {{algebra-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in education, to the study of algebraic structures such as groups, rings, and fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, some having "algebra" in their name, such as commutative algebra, and some not, such as Galois theory. The word ''alge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalization
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation. Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them. However, the parts cannot be generalized into a whole—until a common relation is established among ''all'' parts. This does not mean that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associative Law
In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs. Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations: \begin (2 + 3) + 4 &= 2 + (3 + 4) = 9 \,\\ 2 \times (3 \times 4) &= (2 \times 3) \times 4 = 24 . \end Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds true when performing addition and multiplication on any real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arity
Arity () is the number of arguments or operands taken by a function, operation or relation in logic, mathematics, and computer science. In mathematics, arity may also be named ''rank'', but this word can have many other meanings in mathematics. In logic and philosophy, it is also called adicity and degree. In linguistics, it is usually named valency. Examples The term "arity" is rarely employed in everyday usage. For example, rather than saying "the arity of the addition operation is 2" or "addition is an operation of arity 2" one usually says "addition is a binary operation". In general, the naming of functions or operators with a given arity follows a convention similar to the one used for ''n''-based numeral systems such as binary and hexadecimal. One combines a Latin prefix with the -ary ending; for example: * A nullary function takes no arguments. ** Example: f()=2 * A unary function takes one argument. ** Example: f(x)=2x * A binary function takes two arguments. ** E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
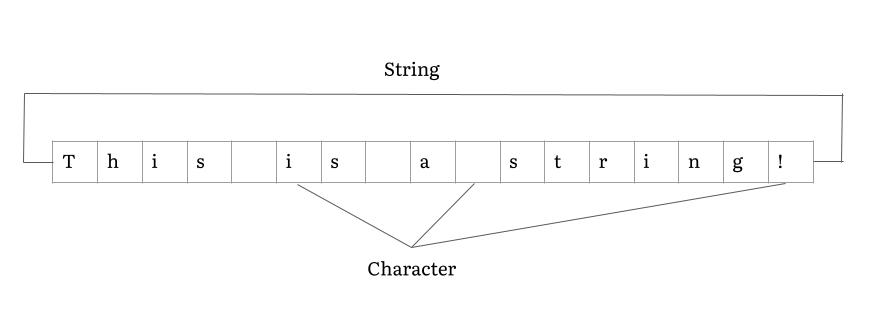
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |