|
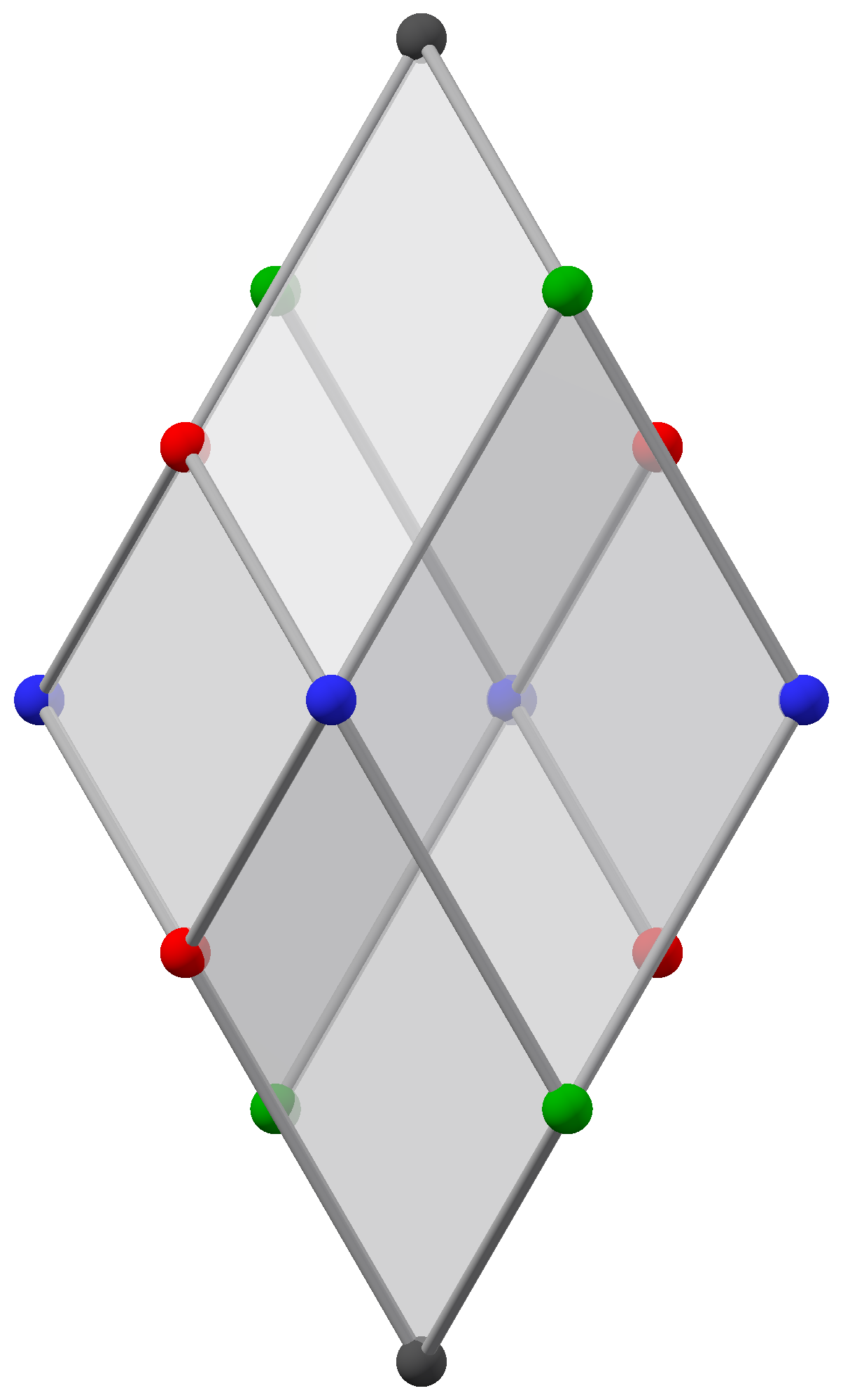
Miquel Configuration
In geometry, the Miquel configuration is a configuration of eight points and six circles in the Euclidean plane, with four points per circle and three circles through each point.. Its Levi graph is the Rhombic dodecahedral graph, the skeleton of both Rhombic dodecahedron and Bilinski dodecahedron. The configuration is related to Miquel's theorem Miquel's theorem is a result in geometry, named after Auguste Miquel, concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles .... References Configurations (geometry) {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miquel Isometric
{{surname ...
Miquel may refer to: * the Catalan form of the given name Michael * Friedrich Anton Wilhelm Miquel (1811–1871), a Dutch botanist * Gérard Miquel (born 1946), a member of the Senate of France * Ignasi Miquel (born 1992), a Spanish football player *Joaquín Miquel (1903–1929), Spanish Olympic runner * Johann von Miquel (1828–1901), a German statesman * Miquel's theorem, a result in geometry, named after Auguste Miquel * Miquel Brown (born 1945), a Canadian actress and disco/soul singer See also *Sant Miquel (other) Sant Miquel (Catalan for Saint Michael) may refer to: Buildings * Sant Miquel, Benedictine monastery in Cruïlles, Monells i Sant Sadurní de l'Heura, Catalonia, Spain *Sant Miquel del Fai, Benedictine monastery in Bigues i Riells, Catalonia, Spain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedral Graph
{{disambiguation ...
Rhombic may refer to: * Rhombus, a quadrilateral whose four sides all have the same length (often called a diamond) *Rhombic antenna, a broadband directional antenna most commonly used on shortwave frequencies * polyhedra formed from rhombuses, such as the rhombic dodecahedron or the rhombic triacontahedron or the rhombic dodecahedral honeycomb or the rhombic icosahedron or the rhombic hexecontahedron or the rhombic enneacontahedron or the trapezo-rhombic dodecahedron * other things that exhibit the shape of a rhombus, such as rhombic tiling, Rhombic Chess, rhombic drive, Rhombic Skaapsteker, rhombic egg eater, rhombic night adder, forest rhombic night adder ''Causus maculatus'' is viper species found mainly in West- and Central Africa. No subspecies are currently recognized. Common names include forest rhombic night adder,Mallow D, Ludwig D, Nilson G. 2003. True Vipers: Natural History and Toxinolo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Configuration (geometry)
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points. Although certain specific configurations had been studied earlier (for instance by Thomas Kirkman in 1849), the formal study of configurations was first introduced by Theodor Reye in 1876, in the second edition of his book ''Geometrie der Lage'', in the context of a discussion of Desargues' theorem. Ernst Steinitz wrote his dissertation on the subject in 1894, and they were popularized by Hilbert and Cohn-Vossen's 1932 book ''Anschauliche Geometrie'', reprinted in English as . Configurations may be studied either as concrete sets of points and lines in a specific geometry, such as the Euclidean or projective planes (these are said to be ''realizable'' in that geometry), or as a type of abstract incidence geometry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In classical Euclidean geometry, a point is a primitive notion that models an exact location in space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space. Being a primitive notion means that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy; for example, ''"there is exactly one line that passes through two different points"''. Points in Euclidean geometry Points, considered within the framework of Euclidean geometry, are one of the most fundamental objects. Euclid originally defined the point as "that which has no part". In two-dimensional Euclidean space, a point is represented by an ordered pair (, ) of numbers, where the first number conventionally represents the horizontal and is often denoted by , and the second number conventionally represents the vertical and is often denoted by . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of parallel lines, and also metrical notions of distance, circles, and angle measurement. The set \mathbb^2 of pairs of real numbers (the real coordinate plane) augmented by appropriate structure often serves as the canonical example. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles in a triangle, and the three cases in which triangles are "equal" (have the same area), among many other topics. Later, the plane was described in a so-called '' Cartesian coordinate system'', a coordinate system that specifies each point uniquely in a plane by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graduate Studies In Mathematics
Graduate Studies in Mathematics (GSM) is a series of graduate-level textbooks in mathematics published by the American Mathematical Society (AMS). The books in this series are published ihardcoverane-bookformats. List of books *1 ''The General Topology of Dynamical Systems'', Ethan Akin (1993, ) *2 ''Combinatorial Rigidity'', Jack Graver, Brigitte Servatius, Herman Servatius (1993, ) *3 ''An Introduction to Gröbner Bases'', William W. Adams, Philippe Loustaunau (1994, ) *4 ''The Integrals of Lebesgue, Denjoy, Perron, and Henstock'', Russell A. Gordon (1994, ) *5 ''Algebraic Curves and Riemann Surfaces'', Rick Miranda (1995, ) *6 ''Lectures on Quantum Groups'', Jens Carsten Jantzen (1996, ) *7 ''Algebraic Number Fields'', Gerald J. Janusz (1996, 2nd ed., ) *8 ''Discovering Modern Set Theory. I: The Basics'', Winfried Just, Martin Weese (1996, ) *9 ''An Invitation to Arithmetic Geometry'', Dino Lorenzini (1996, ) *10 ''Representations of Finite and Compact Groups'', Barry Simon (199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levi Graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure.. See in particulap. 181 From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942. The Levi graph of a system of points and lines usually has girth at least six: Any 4- cycles would correspond to two lines through the same two points. Conversely any bipartite graph with girth at least six can be viewed as the Levi graph of an abstract incidence structure. Levi graphs of configurations are biregular, and every biregular graph with girth at least six can be viewed as the Levi graph of an abstract configuration.. Levi graphs may also be defined for other types of incidence structure, such as the incidences between points and planes in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet correspond t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilinski Dodecahedron
In geometry, the Bilinski dodecahedron is a Convex set, convex polyhedron with twelve Congruence (geometry), congruent golden rhombus faces. It has the same topology but a different geometry than the face-transitive rhombic dodecahedron. It is a parallelohedron. History This shape appears in a book by John Lodge Cowley, labeled as the dodecarhombus. It is named after Stanko Bilinski, who rediscovered it in . Bilinski himself called it the rhombic dodecahedron of the second kind.. Bilinski's discovery corrected a -year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent Rhombus, rhombic faces. Definition and properties Definition The Bilinski dodecahedron is formed by gluing together twelve Congruence (geometry), congruent Golden rhombus, golden rhombi. These are Rhombus, rhombi whose diagonals are in the golden ratio: :\varphi = \approx 1.618~034 . The graph of the resulting polyhedron is Graph isomorphism, isomorphic to the graph of the rhombic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miquel's Theorem
Miquel's theorem is a result in geometry, named after Auguste Miquel, concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles in Euclidean geometry due to Miquel, whose work was published in Liouville's newly founded journal ''Journal de mathématiques pures et appliquées''. Formally, let ''ABC'' be a triangle, with arbitrary points ''A´'', ''B´'' and ''C´'' on sides ''BC'', ''AC'', and ''AB'' respectively (or their extensions). Draw three circumcircles (Miquel's circles) to triangles ''AB´C´'', ''A´BC´'', and ''A´B´C''. Miquel's theorem states that these circles intersect in a single point ''M'', called the Miquel point. In addition, the three angles ''MA´B'', ''MB´C'' and ''MC´A'' (green in the diagram) are all equal, as are the three supplementary angles ''MA´C'', ''MB´A'' and ''MC´B''. - Wells refers to Miquel's theorem as the pivot theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |