|
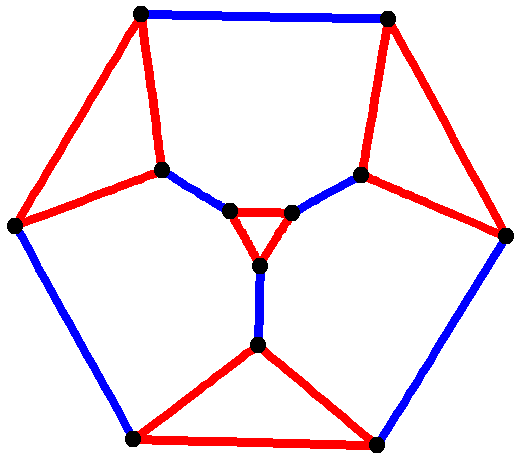
McGee Graph
In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges. The McGee graph is the unique (3,7)-cage (the smallest cubic graph of girth 7). It is also the smallest cubic cage that is not a Moore graph. First discovered by Sachs but unpublished, the graph is named after McGee who published the result in 1960. Then, the McGee graph was proven the unique (3,7)-cage by Tutte in 1966. The McGee graph requires at least eight crossings in any drawing of it in the plane. It is one of three non-isomorphic graphs tied for being the smallest cubic graph that requires eight crossings. Another of these three graphs is the generalized Petersen graph , also known as the Nauru graph. The McGee graph has radius 4, diameter 4, chromatic number 3 and chromatic index 3. It is also a 3- vertex-connected and a 3- edge-connected graph. It has book thickness 3 and queue number 2. Algebraic properties The characteristic polynomial of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
McGee Graph Hamiltonian
McGee or McGees may refer to: People * McGee (surname), a surname of Irish origin, including a list of people with this surname Places United States *McGee, Missouri *McGees, Washington *McGee, West Virginia McGee is an unincorporated community in Taylor County, West Virginia West Virginia is a state in the Appalachian, Mid-Atlantic and Southeastern regions of the United States.The Census Bureau and the Association of American Geographers cl ... Games * ''McGee'' (video game series), a series of computer games for young children See also * * {{disambiguation, geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nauru Graph
In the mathematics, mathematical field of graph theory, the Nauru graph is a symmetric graph, symmetric bipartite graph, bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru. It has chromatic number 2, chromatic index 3, diameter 4, radius 4 and girth 6.Marston Conder, Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002. It is also a 3-k-vertex-connected graph, vertex-connected and 3-k-edge-connected graph, edge-connected graph. It has book thickness 3 and queue number 2. The Nauru graph requires at least eight crossings in any drawing of it in the plane. It is one of three non-isomorphic graphs tied for being the smallest cubic graph that requires eight crossings. Another of these three graphs is the McGee graph, also known as the (3-7)-Cage (graph theory), cage. Construction The Nauru graph is hamiltonian graph, Hamiltonian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acyclic Coloring
In graph theory, an acyclic coloring is a (proper) Graph coloring, vertex coloring in which every 2-chromatic subgraph is Glossary of graph theory, acyclic. The acyclic chromatic number of a Graph (discrete mathematics), graph is the fewest colors needed in any acyclic coloring of . Acyclic coloring is often associated with graphs Graph embedding, embedded on non-plane surfaces. Upper bounds A(''G'') ≤ 2 if and only if ''G'' is acyclic. Bounds on A(''G'') in terms of Δ(''G''), the Glossary of graph theory, maximum degree of ''G'', include the following: * A(''G'') ≤ 4 if Δ(''G'') = 3. * A(''G'') ≤ 5 if Δ(''G'') = 4. * A(''G'') ≤ 7 if Δ(''G'') = 5. * A(''G'') ≤ 12 if Δ(''G'') = 6. A milestone in the study of acyclic coloring is the following affirmative answer to a conjecture of Grünbaum: :Theorem A(''G'') ≤ 5 if ''G'' is planar graph. introduced acyclic coloring and acyclic chromatic number, and conjectured the result in the above theorem. Borodin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crossing Number (graph Theory)
In graph theory, the crossing number of a graph is the lowest number of edge crossings of a plane drawing of the graph . For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing. The study of crossing numbers originated in Turán's brick factory problem, in which Pál Turán asked for a factory plan that minimized the number of crossings between tracks connecting brick kilns to storage sites. Mathematically, this problem can be formalized as asking for the crossing number of a complete bipartite graph. The same problem arose independently in sociology at approximately the same time, in connection with the construction of sociograms. Turán's conjectured formula for the crossing numbers of complete bipartite graphs remains unproven, as does an analogous formu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex-transitive Graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph in which, given any two vertices and of , there is some automorphism :f : G \to G\ such that :f(v_1) = v_2.\ In other words, a graph is vertex-transitive if its automorphism group acts transitively on its vertices.. A graph is vertex-transitive if and only if its graph complement is, since the group actions are identical. Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's graph). Finite examples Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected cycles) are also ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The characteristic polynomial of an endomorphism of a finite-dimensional vector space is the characteristic polynomial of the matrix of that endomorphism over any base (that is, the characteristic polynomial does not depend on the choice of a basis). The characteristic equation, also known as the determinantal equation, is the equation obtained by equating the characteristic polynomial to zero. In spectral graph theory, the characteristic polynomial of a graph is the characteristic polynomial of its adjacency matrix. Motivation In linear algebra, eigenvalues and eigenvectors play a fundamental role, since, given a linear transformation, an eigenvector is a vector whose direction is not changed by the transformation, and the corresponding eigenva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queue Number
In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number (book thickness) using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings. Definition A queue layout of a given graph is defined by a total ordering of the vertices of the graph together with a partition of the edges into a number of "queues". The set of edges in each queue is required to avoid edges that are properly nested: if and are two edges in the same queue, then it should not be possible to have in the vertex ordering. The queue number of a graph is the minimum number of queues in a queue layout.. Equivalently, from a queue layout, one could process the edges in a single queue using a queue data structure, by considering the vertices in their given ordering, and when reaching a vertex, dequeueing all edges for which it is the second endpoint followed by enqueueing all edges for which it is the first en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Book Thickness
In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings into a ''book'', a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the ''spine'', and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number. Every graph with vertices has book thickness at most \lceil n/2\rceil, and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-edge-connected Graph
In graph theory, a connected graph is -edge-connected if it remains connected whenever fewer than edges are removed. The edge-connectivity of a graph is the largest for which the graph is -edge-connected. Edge connectivity and the enumeration of -edge-connected graphs was studied by Camille Jordan in 1869. Formal definition Let G = (V, E) be an arbitrary graph. If subgraph G' = (V, E \setminus X) is connected for all X \subseteq E where , X, < k, then ''G'' is ''k''-edge-connected. The edge connectivity of is the maximum value ''k'' such that ''G'' is ''k''-edge-connected. The smallest set ''X'' whose removal disconnects ''G'' is a in ''G''. The edge connectivity version of provi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-vertex-connected Graph
In graph theory, a connected graph is said to be -vertex-connected (or -connected) if it has more than vertices and remains connected whenever fewer than vertices are removed. The vertex-connectivity, or just connectivity, of a graph is the largest for which the graph is -vertex-connected. Definitions A graph (other than a complete graph) has connectivity ''k'' if ''k'' is the size of the smallest subset of vertices such that the graph becomes disconnected if you delete them. Complete graphs are not included in this version of the definition since they cannot be disconnected by deleting vertices. The complete graph with ''n'' vertices has connectivity ''n'' − 1, as implied by the first definition. An equivalent definition is that a graph with at least two vertices is ''k''-connected if, for every pair of its vertices, it is possible to find ''k'' vertex-independent paths connecting these vertices; see Menger's theorem . This definition produces the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Index
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most different colors, for a given value of , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three. By Vizing's theorem, the number of colors needed to edge color a simple graph is either its maximum degree or . For some graphs, such as bipartite graphs and high-degree planar graphs, the number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Number
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |