|
Mathieu Lewin
Mathieu Lewin (born 14 November 1977 in Senlis, Oise, France) is a French mathematician and mathematical physicist who deals with partial differential equations, mathematical quantum field theory and mathematics of quantum mechanical many-body systems. Biography Lewin studied mathematics at the École normale supérieure de Cachan, receiving his master's degree in 2000. He then received his PhD in 2004 at the Paris Dauphine University (Dauphine-Paris) PhD under the direction of Éric Séré. His dissertation was titled ''Some nonlinear models in quantum mechanics''. From 2004 to 2005 he was a postdoctoral fellow at the University of Copenhagen under Jan Philip Solovej. From 2005, he conducted research for the Centre national de la recherche scientifique (CNRS) at the University of Cergy-Pontoise, then at the Paris-Dauphine university. In July 2012, he has been awarded an EMS Prize "for his ground breaking work in rigorous aspects of quantum chemistry, mean field approximati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Senlis
Senlis () is a commune in the northern French department of Oise, Hautes de France. The monarchs of the early French dynasties lived in Senlis, attracted by the proximity of the Chantilly forest. It is known for its Gothic cathedral and other historical monuments. Its inhabitants are called "Senlisiens" and "Senlisiennes". Geography Senlis is situated on the river Nonette, between the forests of Chantilly and d'Ermenonville in the South and d'Halatte on the North. It is located 40 kilometers to the north of Paris, 44 km from Beauvais and 79 km from Amiens. The highest point of the town (140m) lies at the heart of the forest Halatte and the lowest point is located on the banks of the Nonette, west of the city. Geologically, the area is occupied by a vast limestone plateau of the Lutetian covered mostly in silt. History Senlis was known in early Roman imperial times as Augustomagus and later as Civitas Silvanectium ("City of the Silvanectes"). During the 3rd cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as '' geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1977 Births
Events January * January 8 – 1977 Moscow bombings, Three bombs explode in Moscow within 37 minutes, killing seven. The bombings are attributed to an Armenian separatist group. * January 10 – Mount Nyiragongo erupts in eastern Zaire (now the Democratic Republic of the Congo). * January 17 ** 49 marines from the and are killed as a result of a collision in Barcelona harbour, Spain. * January 18 ** Scientists identify a previously unknown Bacteria, bacterium as the cause of the mysterious Legionnaires' disease. ** Australia's worst Granville rail disaster, railway disaster at Granville, a suburb of Sydney, leaves 83 people dead. ** SFR Yugoslavia Prime minister Džemal Bijedić, his wife and 6 others are killed in a plane crash in Bosnia and Herzegovina. * January 19 – An Ejército del Aire CASA C-207 Azor, CASA C-207C Azor (registration T.7-15) plane crashes into the side of a mountain near Chiva, Valencia, Chiva, on approach to Valencia Airport in Spain, killing all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advances In Mathematics
''Advances in Mathematics'' is a peer-reviewed scientific journal covering research on pure mathematics. It was established in 1961 by Gian-Carlo Rota. The journal publishes 18 issues each year, in three volumes. At the origin, the journal aimed at publishing articles addressed to a broader "mathematical community", and not only to mathematicians in the author's field. Herbert Busemann writes, in the preface of the first issue, "The need for expository articles addressing either all mathematicians or only those in somewhat related fields has long been felt, but little has been done outside of the USSR. The serial publication ''Advances in Mathematics'' was created in response to this demand." Abstracting and indexing The journal is abstracted and indexed in: * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models. The diversity of systems and phenomena available for study makes condensed matt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
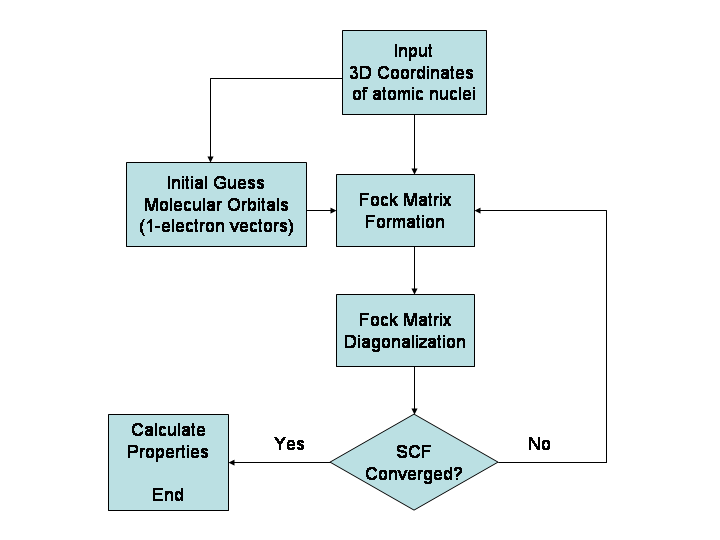
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distributi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multi-configurational Self-consistent Field
Multi-configurational self-consistent field (MCSCF) is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate (e.g., for molecular ground states which are quasi-degenerate with low-lying excited states or in bond-breaking situations). It uses a linear combination of configuration state functions (CSF), or configuration determinants, to approximate the exact electronic wavefunction of an atom or molecule. In an MCSCF calculation, the set of coefficients of both the CSFs or determinants and the basis functions in the molecular orbitals are varied to obtain the total electronic wavefunction with the lowest possible energy. This method can be considered a combination between configuration interaction (where the molecular orbitals are not varied but the expansion of the wave function) and Hartree–Fock (where there is only one determinant, but the molecular orbitals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of systems of linear equations and their generalizations. The theory is connected to that of analytic functions because the spectral properties of an operator are related to analytic functions of the spectral parameter. Mathematical background The name ''spectral theory'' was introduced by David Hilbert in his original formulation of Hilbert space theory, which was cast in terms of quadratic forms in infinitely many variables. The original spectral theorem was therefore conceived as a version of the theorem on principal axes of an ellipsoid, in an infinite-dimensional setting. The later discovery in quantum mechanics that spectral theory could explain features of atomic spectra was the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Functional Analysis
Nonlinear functional analysis is a branch of mathematical analysis that deals with nonlinear mappings. Topics Its subject matter includes: * generalizations of calculus to Banach spaces * implicit function theorems * fixed-point theorems (Brouwer fixed point theorem, Fixed point theorems in infinite-dimensional spaces, topological degree theory, Jordan separation theorem, Lefschetz fixed-point theorem) * Morse theory and Lusternik–Schnirelmann category theory * methods of complex function theory See also * Functional analysis Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. inner product, norm, topology, etc.) and the linear functions defined ... Notes {{Authority control ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
EMS Prize
The European Mathematical Society (EMS) is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians. The current president is Volker Mehrmann, professor at the Institute for Mathematics at the Technical University of Berlin. Goals The Society seeks to serve all kinds of mathematicians in universities, research institutes and other forms of higher education. Its aims are to #Promote mathematical research, both pure and applied, #Assist and advise on problems of mathematical education, #Concern itself with the broader relations of mathematics to society, #Foster interaction between mathematicians of different countries, #Establish a sense of identity amongst European mathematicians, #Represent the mathematical community in supra-national institutions. The EMS is itself an Affiliate Member of the International Mathematical Union and an Associate Mem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |