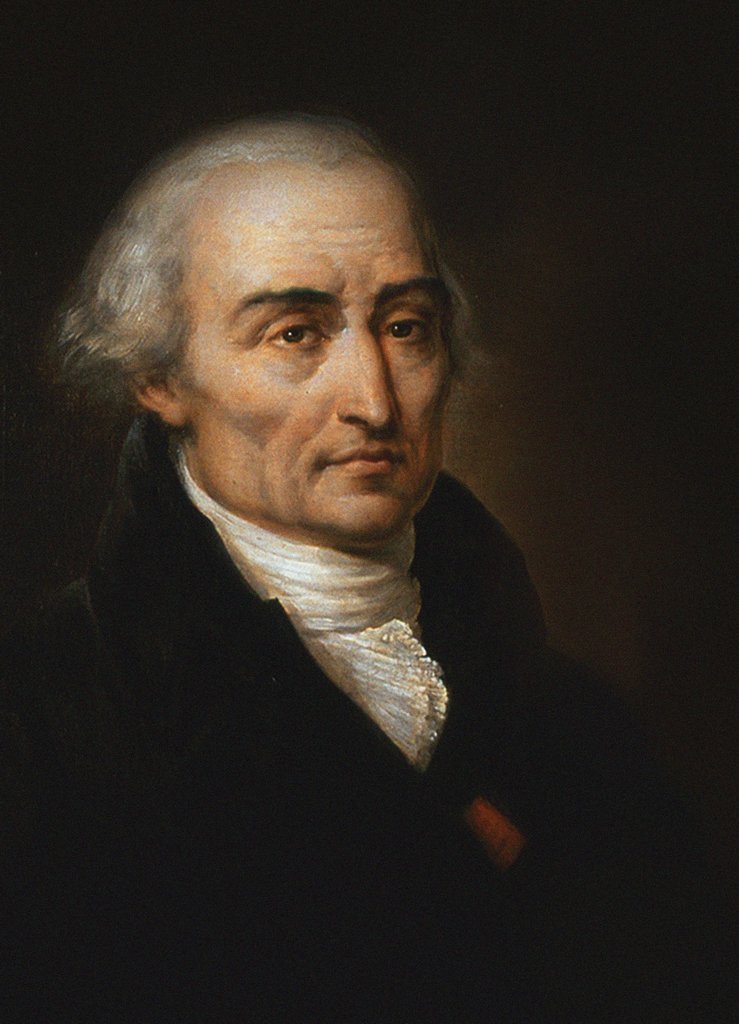|
Mathematical Physics
Mathematical physics refers to the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and for the formulation of physical theories". An alternative definition would also include those mathematics that are inspired by physics (also known as physical mathematics). Scope There are several distinct branches of mathematical physics, and these roughly correspond to particular historical periods. Classical mechanics The rigorous, abstract and advanced reformulation of Newtonian mechanics adopting the Lagrangian mechanics and the Hamiltonian mechanics even in the presence of constraints. Both formulations are embodied in analytical mechanics and lead to understanding the deep interplay of the notions of symmetry (physics), symmetry and conservation law, con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, craft, science and technology h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Theory
In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to ''plasticity'', in which the object fails to do so and instead remains in its deformed state. The physical reasons for elastic behavior can be quite different for different materials. In metals, the atomic lattice changes size and shape when forces are applied (energy is added to the system). When forces are removed, the lattice goes back to the original lower energy state. For rubbers and other polymers, elasticity is caused by the stretching of polymer chains when forces are applied. Hooke's law states that the force required to deform elastic objects should be directly proportional to the distanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's Principia of 1687. The name "celestial mechanics" is more recent than that. Newton wrote that the field should be called "rational mechanics." The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term "celestial mechanics." Prior to Kepler there was little connection between exact, quantitative prediction of planetary positions, using geometrical or arithmetical techniques, and contemporary discussions of the physical causes of the planets' motion. Johannes Kepler Johannes Kepler (1571–1630) was the first to closely integrate the predictive geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrodynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph-Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian and , later naturalized |
Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and Mathematical notation, notation, including the notion of a function (mathematics), mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean Le Rond D'Alembert
Jean-Baptiste le Rond d'Alembert (; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the '' Encyclopédie''. D'Alembert's formula for obtaining solutions to the wave equation is named after him. The wave equation is sometimes referred to as d'Alembert's equation, and the fundamental theorem of algebra is named after d'Alembert in French. Early years Born in Paris, d'Alembert was the natural son of the writer Claudine Guérin de Tencin and the chevalier Louis-Camus Destouches, an artillery officer. Destouches was abroad at the time of d'Alembert's birth. Days after birth his mother left him on the steps of the church. According to custom, he was named after the patron saint of the church. D'Alembert was placed in an orphanage for foundling children, but his father found him and placed him with the wife of a glazier, Madame Rousseau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Analysis
Vector calculus, or vector analysis, is concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space \mathbb^3. The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow. Vector calculus was developed from quaternion analysis by J. Willard Gibbs and Oliver Heaviside near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson in their 1901 book, '' Vector Analysis''. In the conventional form using cross products, vector calculus does not generalize to higher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Theory
In mathematics and mathematical physics, potential theory is the study of harmonic functions. The term "potential theory" was coined in 19th-century physics when it was realized that two fundamental forces of nature known at the time, namely gravity and the electrostatic force, could be modeled using functions called the gravitational potential and electrostatic potential, both of which satisfy Poisson's equation—or in the vacuum, Laplace's equation. There is considerable overlap between potential theory and the theory of Poisson's equation to the extent that it is impossible to draw a distinction between these two fields. The difference is more one of emphasis than subject matter and rests on the following distinction: potential theory focuses on the properties of the functions as opposed to the properties of the equation. For example, a result about the singularities of harmonic functions would be said to belong to potential theory whilst a result on how the solution dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |