|
Mass Point Geometry
Mass point geometry, colloquially known as mass points, is a problem-solving technique in geometry which applies the physical principle of the center of mass to geometry problems involving triangles and intersecting cevians. All problems that can be solved using mass point geometry can also be solved using either similar triangles, vectors, or area ratios, but many students prefer to use mass points. Though modern mass point geometry was developed in the 1960s by New York high school students, the concept has been found to have been used as early as 1827 by August Ferdinand Möbius in his theory of homogeneous coordinates. Definitions The theory of mass points is defined according to the following definitions:H. S. M. Coxeter, ''Introduction to Geometry'', pp. 216-221, John Wiley & Sons, Inc. 1969 * Mass Point - A mass point is a pair (m, P), also written as mP, including a mass, m, and an ordinary point, P on a plane. * Coincidence - We say that two points mP and nQ coinc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Altitude
Altitude or height (also sometimes known as depth) is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The exact definition and reference datum varies according to the context (e.g., aviation, geometry, geographical survey, sport, or atmospheric pressure). Although the term ''altitude'' is commonly used to mean the height above sea level of a location, in geography the term elevation is often preferred for this usage. Vertical distance measurements in the "down" direction are commonly referred to as depth. In aviation In aviation, the term altitude can have several meanings, and is always qualified by explicitly adding a modifier (e.g. "true altitude"), or implicitly through the context of the communication. Parties exchanging altitude information must be clear which definition is being used. Aviation altitude is measured using either mean sea level (MSL) or local ground level (above ground level, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
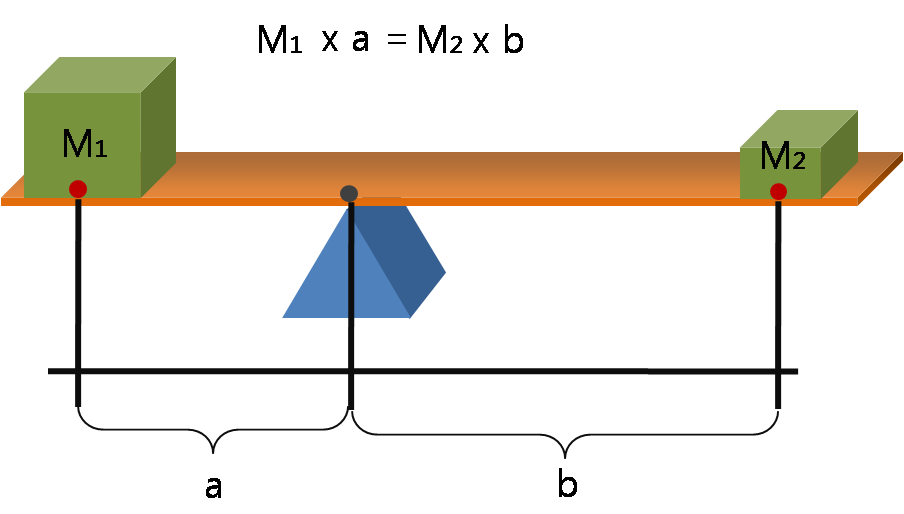
Lever
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or '' fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load and effort, the lever is divided into three types. Also, leverage is mechanical advantage gained in a system. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage. The ratio of the output force to the input force is the mechanical advantage of the lever. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English around 1300 from Old French, in which the word was ''levier''. This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to the Latin ''levare'', itself from the adjective ''levis'', meaning "light" (as in "not heavy") ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinates (mathematics)
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or ''barycenter'') of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex. Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity. Barycentric coordina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Bisector Theorem
In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle. Theorem Consider a triangle ''ABC''. Let the angle bisector of angle ''A'' intersect side ''BC'' at a point ''D'' between ''B'' and ''C''. The angle bisector theorem states that the ratio of the length of the line segment ''BD'' to the length of segment ''CD'' is equal to the ratio of the length of side ''AB'' to the length of side ''AC'': :=, and conversely, if a point ''D'' on the side ''BC'' of triangle ''ABC'' divides ''BC'' in the same ratio as the sides ''AB'' and ''AC'', then ''AD'' is the angle bisector of angle ''∠ A''. The generalized angle bisector theorem states that if ''D'' lies on the line ''BC'', then :=. This reduces to the previous version if ''AD'' is the bisector of ''∠ BA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Menelaus's Theorem
Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Suppose we have a triangle ''ABC'', and a transversal line that crosses ''BC'', ''AC'', and ''AB'' at points ''D'', ''E'', and ''F'' respectively, with ''D'', ''E'', and ''F'' distinct from ''A'', ''B'', and ''C''. A weak version of the theorem states that : \frac \times \frac \times \frac = 1, where '', AB, '' is taken to be the ordinary length of segment ''AB'': a positive value. The theorem can be strengthened to a statement about signed lengths of segments, which provides some additional information about the relative order of collinear points. Here, the length ''AB'' is taken to be positive or negative according to whether ''A'' is to the left or right of ''B'' in some fixed orientation of the line; for example, ''AF''/''FB'' is defined as having positive value when ''F'' is between ''A'' and ''B'' and negative otherwise. The signed version of Menelaus's theorem sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ceva's Theorem
In Euclidean geometry, Ceva's theorem is a theorem about triangles. Given a triangle , let the lines be drawn from the vertices to a common point (not on one of the sides of ), to meet opposite sides at respectively. (The segments are known as cevians.) Then, using signed lengths of segments, :\frac \cdot \frac \cdot \frac = 1. In other words, the length is taken to be positive or negative according to whether is to the left or right of in some fixed orientation of the line. For example, is defined as having positive value when is between and and negative otherwise. Ceva's theorem is a theorem of affine geometry, in the sense that it may be stated and proved without using the concepts of angles, areas, and lengths (except for the ratio of the lengths of two line segments that are collinear). It is therefore true for triangles in any affine plane over any field. A slightly adapted converse is also true: If points are chosen on respectively so that : \frac \c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cevian
In geometry, a cevian is a line that intersects both a triangle's vertex, and also the side that is opposite to that vertex. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name. Length Stewart's theorem The length of a cevian can be determined by Stewart's theorem: in the diagram, the cevian length is given by the formula :\,b^2m + c^2n = a(d^2 + mn). Less commonly, this is also represented (with some rearrangement) by the following mnemonic: :\underset = \!\!\!\!\!\! \underset Median If the cevian happens to be a median (thus bisecting a side), its length can be determined from the formula :\,m(b^2 + c^2) = a(d^2 + m^2) or :\,2(b^2 + c^2) = 4d^2 + a^2 since :\,a = 2m. Hence in this case :d= \frac\sqrt2 . Angle bisector If the cevian happens to be an angle bisector, its length obeys the formulas :\,(b + c)^2 = a^2 \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Points8
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Points7
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Points6
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Points5
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |