|
Madelung Constant
The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. It is named after Erwin Madelung, a German physicist. Because the anions and cations in an ionic solid attract each other by virtue of their opposing charges, separating the ions requires a certain amount of energy. This energy must be given to the system in order to break the anion–cation bonds. The energy required to break these bonds for one mole of an ionic solid under standard conditions is the lattice energy. Formal expression The Madelung constant allows for the calculation of the electric potential V_i of all ions of the lattice felt by the ion at position r_i :V_i = \frac \sum_ \frac\,\! where r_ = , r_i-r_j, is the distance between the i^ and the j^ ion. In addition, :z_j = number of charges of the j^ ion :e= 1.6022 C :4\pi \epsilon_0= . If the distances r_ are normalized to the nearest neighbor distance r_0, the potent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditionally Convergent
In mathematics, a series or integral is said to be conditionally convergent if it converges, but it does not converge absolutely. Definition More precisely, a series of real numbers \sum_^\infty a_n is said to converge conditionally if \lim_\,\sum_^m a_n exists (as a finite real number, i.e. not \infty or -\infty), but \sum_^\infty \left, a_n\ = \infty. A classic example is the alternating harmonic series given by 1 - + - + - \cdots =\sum\limits_^\infty , which converges to \ln (2), but is not absolutely convergent (see Harmonic series). Bernhard Riemann proved that a conditionally convergent series may be rearranged to converge to any value at all, including ∞ or −∞; see ''Riemann series theorem''. The Lévy–Steinitz theorem identifies the set of values to which a series of terms in R''n'' can converge. A typical conditionally convergent integral is that on the non-negative real axis of \sin (x^2) (see Fresnel integral). See also *Absolute convergen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cation-anion Radius Ratio
Anions are larger than cations. Large sized anions occupy lattice sites, while small sized cations are found in voids. The ratio of radius of cation to anion is called radius ratio. In condensed matter physics and inorganic chemistry the cation-anion radius ratio (also: radius ratio rule) is the ratio of the ionic radius of the cation to the ionic radius of the anion in a cation-anion compound. This is simply given by r_ / r_. According to Pauling's rules for crystal structures, the allowed size of the cation for a given structure is determined by the critical radius ratio. If the cation is too small, then it will attract the anions into each other and they will collide hence the compound will be unstable due to anion-anion repulsion; this occurs when the radius ratio drops below 0.155. At the stability limit the cation is touching all the anions and the anions are just touching at their edges (radius ratio = 0.155). For radius ratios greater than 0.155, the compound may be sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Number
In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion/molecule/atom is called a ligand. This number is determined somewhat differently for molecules than for crystals. For molecules and polyatomic ions the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, r(NH3)2Cl2Br2sup>− has Cr3+ as its central cation, which has a coordination number of 6 and is described as ''hexacoordinate''. The common coordination numbers are 4, 6 and 8. Molecules, polyatomic ions and coordination complexes In chemistry, coordination number, defined originally in 1893 by Alfred Werner, is the total number of neighbors of a central atom in a molecule or ion. The concept is most commonly applied to coordin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
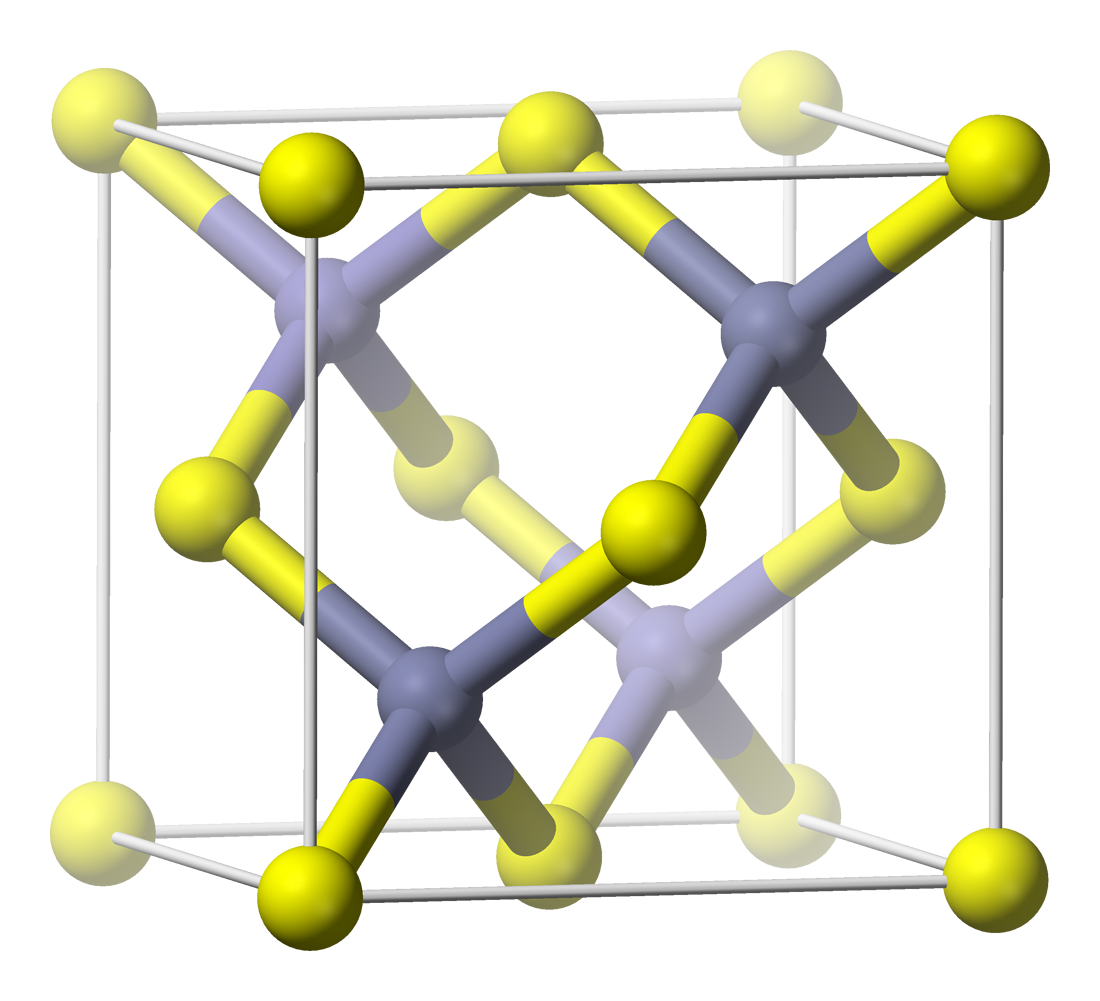
Fluorite Structure
In solid state chemistry, the fluorite structure refers to a common motif for compounds with the formula MX2. The X ions occupy the eight tetrahedral interstitial sites whereas M ions occupy the regular sites of a face-centered cubic (FCC) structure. Many compounds, notably the common mineral fluorite (CaF2), adopt this structure. Many compounds with formula M2X have an antifluorite structure. In these the locations of the anions and cations are reversed relative to fluorite (an anti-structure); the anions occupy the FCC regular sites whereas the cations occupy the tetrahedral interstitial sites. For example, Magnesium silicide, Mg2Si, has a lattice parameter of 6.338 Å with magnesium cations occupying the tetrahedral interstitial sites, in which each silicide anion is surrounded by eight magnesium cations and each magnesium cation is surrounded by four silicide anions in a tetrahedral fashion. File:Fluorite Structure.jpg, The fluorite structure of calcium fluoride CaF2. File:Anti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphalerite
Sphalerite (sometimes spelled sphaelerite) is a sulfide mineral with the chemical formula . It is the most important ore of zinc. Sphalerite is found in a variety of deposit types, but it is primarily in Sedimentary exhalative deposits, sedimentary exhalative, Carbonate-hosted lead-zinc ore deposits, Mississippi-Valley type, and Volcanogenic massive sulfide ore deposit, volcanogenic massive sulfide deposits. It is found in association with galena, chalcopyrite, pyrite (and other sulfide mineral, sulfides), calcite, dolomite (mineral), dolomite, quartz, rhodochrosite, and fluorite. German geologist Ernst Friedrich Glocker discovered sphalerite in 1847, naming it based on the Greek word ''sphaleros'', meaning "deceiving", due to the difficulty of identifying the mineral. In addition to zinc, sphalerite is an ore of cadmium, gallium, germanium, and indium. Miners have been known to refer to sphalerite as ''zinc blende'', ''black-jack'', and ''ruby blende''. Marmatite is an opaque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rocksalt
Halite (), commonly known as rock salt, is a type of salt, the mineral (natural) form of sodium chloride ( Na Cl). Halite forms isometric crystals. The mineral is typically colorless or white, but may also be light blue, dark blue, purple, pink, red, orange, yellow or gray depending on inclusion of other materials, impurities, and structural or isotopic abnormalities in the crystals. It commonly occurs with other evaporite deposit minerals such as several of the sulfates, halides, and borates. The name ''halite'' is derived from the Ancient Greek word for "salt", ἅλς (''háls''). Occurrence Halite dominantly occurs within sedimentary rocks where it has formed from the evaporation of seawater or salty lake water. Vast beds of sedimentary evaporite minerals, including halite, can result from the drying up of enclosed lakes and restricted seas. Such salt beds may be hundreds of meters thick and underlie broad areas. Halite occurs at the surface today in playas in regio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the Crystal_structure#Unit_cell, unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called Close-packing_of_equal_spheres, ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive_cell, primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one Lattice_(group), lattice point on each corner of the cube; this means each simple cubic unit cell has in total one latt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ewald Summation
Ewald summation, named after Paul Peter Ewald, is a method for computing long-range interactions (e.g. electrostatic interactions) in periodic systems. It was first developed as the method for calculating electrostatic energies of ionic crystals, and is now commonly used for calculating long-range interactions in computational chemistry. Ewald summation is a special case of the Poisson summation formula, replacing the summation of interaction energies in real space with an equivalent summation in Fourier space. In this method, the long-range interaction is divided into two parts: a short-range contribution, and a long-range contribution which does not have a singularity. The short-range contribution is calculated in real space, whereas the long-range contribution is calculated using a Fourier transform. The advantage of this method is the rapid convergence of the energy compared with that of a direct summation. This means that the method has high accuracy and reasonable speed when co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Transform
In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in the original function space. The transformed function can generally be mapped back to the original function space using the ''inverse transform''. General form An integral transform is any transform ''T'' of the following form: :(Tf)(u) = \int_^ f(t)\, K(t, u)\, dt The input of this transform is a function ''f'', and the output is another function ''Tf''. An integral transform is a particular kind of mathematical operator. There are numerous useful integral transforms. Each is specified by a choice of the function K of two variables, the kernel function, integral kernel or nucleus of the transform. Some kernels have an associated ''inverse kernel'' K^( u,t ) which (roughly speaking) yields an inverse transform: :f(t) = \int_^ (Tf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent. The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of singularities. The case of several complex variables is rather different, since singularities then need not be isolated points, and its investigation was a major reason for the development of sheaf cohomology. Initial discussion Suppose ''f'' is an analytic function defined on a non-empty open subset ''U'' of the complex plane If ''V'' is a larger open subset of containing ''U'', and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jonathan Borwein
Jonathan Michael Borwein (20 May 1951 – 2 August 2016) was a Scottish mathematician who held an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. He was a close associate of David H. Bailey, and they have been prominent public advocates of experimental mathematics. Borwein's interests spanned pure mathematics (analysis), applied mathematics (optimization), computational mathematics (numerical and computational analysis), and high performance computing. He authored ten books, including several on experimental mathematics, a monograph on convex functions, and over 400 refereed articles. He was a co-founder in 1995 of software company MathResources, consulting and producing interactive software primarily for school and university mathematics. Borwein was also an expert on the number pi and especially its computation. Early life and education Borwein was born in St. Andrews, Scotland in 1951 into a Jewish family. His father was mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |