|
Multivariate Hypergeometric Distribution
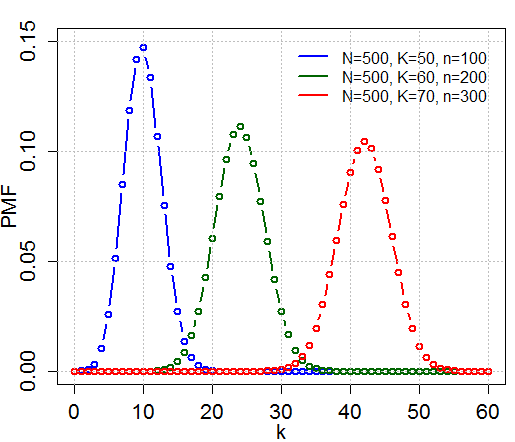
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population (''sampling without replacement'' from a finite population). A random variable X follows the hyper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
WikiProject Probability
A WikiProject, or Wikiproject, is a Wikimedia movement affinity group for contributors with shared goals. WikiProjects are prevalent within the largest wiki, Wikipedia, and exist to varying degrees within sister projects such as Wiktionary, Wikiquote, Wikidata, and Wikisource. They also exist in different languages, and translation of articles is a form of their collaboration. During the COVID-19 pandemic, CBS News noted the role of Wikipedia's WikiProject Medicine in maintaining the accuracy of articles related to the disease. Another WikiProject that has drawn attention is WikiProject Women Scientists, which was profiled by '' Smithsonian'' for its efforts to improve coverage of women scientists which the profile noted had "helped increase the number of female scientists on Wikipedia from around 1,600 to over 5,000". On Wikipedia Some Wikipedia WikiProjects are substantial enough to engage in cooperative activities with outside organizations relevant to the field at issue. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marbles
A marble is a small spherical object often made from glass, clay, steel, plastic, or agate. They vary in size, and most commonly are about in diameter. These toys can be used for a variety of games called ''marbles'', as well being placed in marble runs or races, or created as a form of art. They are often collected, both for nostalgia and for their aesthetic colors. Sizes may range from less than to over , while some art glass marbles for display purposes are over wide. In the North of England the objects and the game are called "taws", with larger taws being called "bottle washers" after the use of a marble in Codd-neck bottles, which were often collected for play. Games History In the early twentieth century, small balls of stone from about 2500 BCE, identified by archaeologists as marbles, were found by excavation near Mohenjo-daro, in a site associated with the Indus Valley civilization. Marbles are often mentioned in Roman literature, as in Ovid's poem "Nux" (whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Prior
In Bayesian probability theory, if the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function p(x \mid \theta). A conjugate prior is an algebraic convenience, giving a closed-form expression for the posterior; otherwise, numerical integration may be necessary. Further, conjugate priors may give intuition by more transparently showing how a likelihood function updates a prior distribution. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory. Howard Raiffa and Robert Schlaifer. ''Applied Statistical Decision Theory''. Division of Research, Graduate School of Business Administration, Harvard University, 1961. A similar concept had been discovered independently by George ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta-binomial Distribution
In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of ''n'' trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data. The beta-binomial is a one-dimensional version of the Dirichlet-multinomial distribution as the binomial and beta distributions are univariate versions of the multinomial and Dirichlet distributions respectively. The special case where ''α'' and ''β'' are integers is also known as the negative hypergeometric distribution. Motivation and derivation As a compound dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noncentral Hypergeometric Distribution
In statistics, the hypergeometric distribution is the discrete probability distribution generated by picking colored balls at random from an urn without replacement. Various generalizations to this distribution exist for cases where the picking of colored balls is biased so that balls of one color are more likely to be picked than balls of another color. This can be illustrated by the following example. Assume that an opinion poll is conducted by calling random telephone numbers. Unemployed people are more likely to be home and answer the phone than employed people are. Therefore, unemployed respondents are likely to be over-represented in the sample. The probability distribution of employed versus unemployed respondents in a sample of ''n'' respondents can be described as a noncentral hypergeometric distribution. The description of biased urn models is complicated by the fact that there is more than one noncentral hypergeometric distribution. Which distribution one gets dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probability distribution of a random variable which takes the value 1 with probability p and the value 0 with probability q = 1-p. Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are boolean-valued: a single bit whose value is success/yes/ true/one with probability ''p'' and failure/no/false/zero with probability ''q''. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and ''p'' would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and ''p'' would be the probability of tails). In particular, unfair coins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher's Exact Test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables. Although in practice it is employed when sample sizes are small, it is valid for all sample sizes. It is named after its inventor, Ronald Fisher, and is one of a class of exact tests, so called because the significance of the deviation from a null hypothesis (e.g., P-value) can be calculated exactly, rather than relying on an approximation that becomes exact in the limit as the sample size grows to infinity, as with many statistical tests. Fisher is said to have devised the test following a comment from Muriel Bristol, who claimed to be able to detect whether the tea or the milk was added first to her cup. He tested her claim in the " lady tasting tea" experiment. Purpose and scope The test is useful for categorical data that result from classifying objects in two different ways; it is used to examine the significance of the association (contingency) between the two kinds of cla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Annals Of Statistics
The ''Annals of Statistics'' is a peer-reviewed statistics journal published by the Institute of Mathematical Statistics. It was started in 1973 as a continuation in part of the ''Annals of Mathematical Statistics (1930)'', which was split into the ''Annals of Statistics'' and the '' Annals of Probability''. The journal CiteScore is 5.8, and its SCImago Journal Rank is 5.877, both from 2020. Articles older than 3 years are available on JSTOR, and all articles since 2004 are freely available on the arXiv. Editorial board The following persons have been editors of the journal: * Ingram Olkin (1972–1973) * I. Richard Savage (1974–1976) * Rupert Miller (1977–1979) * David V. Hinkley (1980–1982) * Michael D. Perlman (1983–1985) * Willem van Zwet (1986–1988) * Arthur Cohen (1988–1991) * Michael Woodroofe (1992–1994) * Larry Brown and John Rice (1995–1997) * Hans-Rudolf Künsch and James O. Berger (1998–2000) * John Marden and Jon A. Wellner (2001–2003) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The American Statistical Association
The ''Journal of the American Statistical Association (JASA)'' is the primary journal published by the American Statistical Association, the main professional body for statisticians in the United States. It is published four times a year in March, June, September and December by Taylor & Francis, Ltd on behalf of the American Statistical Association. As a statistics journal it publishes articles primarily focused on the application of statistics, statistical theory and methods in economic, social, physical, engineering, and health sciences. The journal also includes reviews of academic books which are important to the advancement of the field. It had an impact factor of 2.063 in 2010, tenth highest in the "Statistics and Probability" category of '' Journal Citation Reports''. In a 2003 survey of statisticians, the ''Journal of the American Statistical Association'' was ranked first, among all journals, for "Applications of Statistics" and second (after ''Annals of Statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |