|
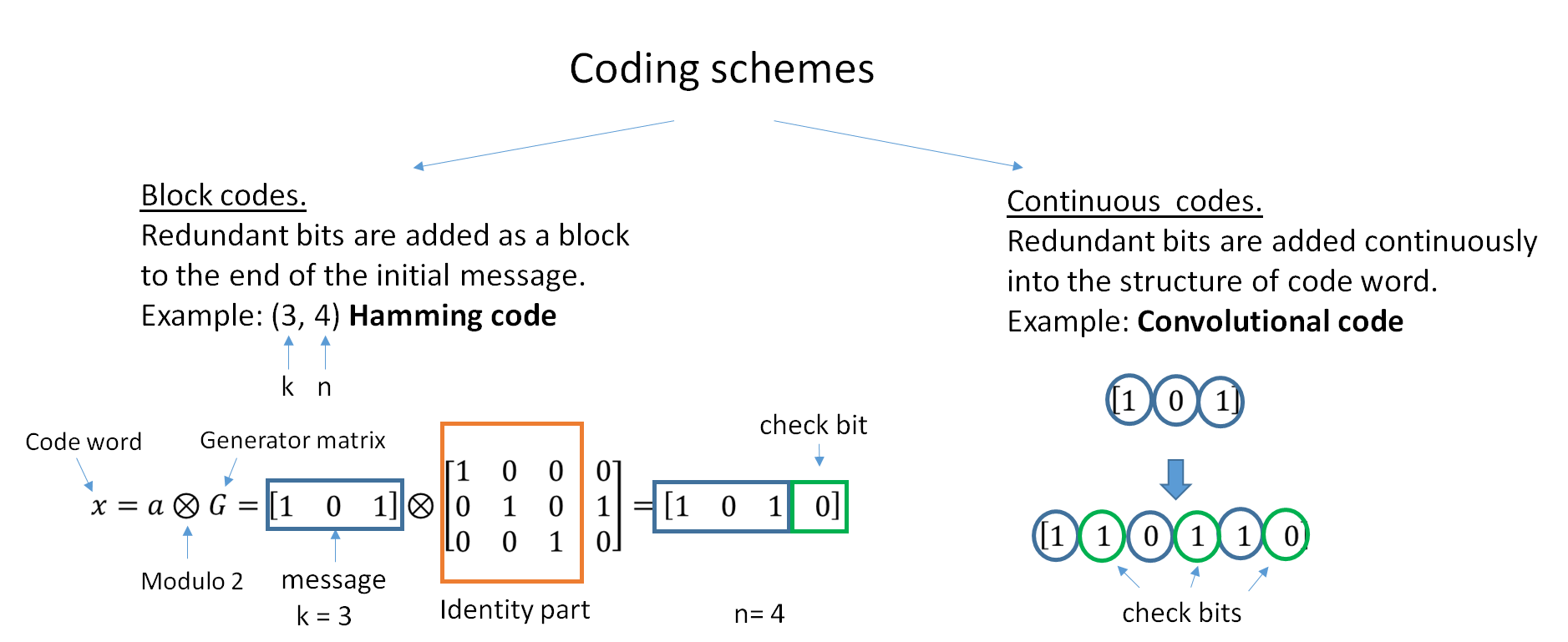
Multidimensional Parity-check Code
A multidimensional parity-check code (MDPC) is a simple type of error correcting code that operates by arranging the message into a multidimensional grid, and calculating a parity digit for each row and column. In general, an ''n''-dimensional parity scheme can correct ''n''/2 errors.{{Citation needed, date=May 2009 Example The two-dimensional parity-check code, usually called the optimal rectangular code, is the most popular form of multidimensional parity-check code. Assume that the goal is to transmit the four-digit message "1234", using a two-dimensional parity scheme. First the digits of the message are arranged in a rectangular pattern: :12 :34 Parity digits are then calculated by summing each column and row separately: :123 :347 :46 The eight-digit sequence "12334746" is the message that is actually transmitted. If any single error occurs during transmission then this error can not only be detected but can also be corrected as well. Let us suppose that the rec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Correcting Code
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity Bit
A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits. The parity bit ensures that the total number of 1-bits in the string is even or odd. Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit's value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Rectangular Code
In telecommunication, a longitudinal redundancy check (LRC), or horizontal redundancy check, is a form of redundancy check that is applied independently to each of a parallel group of bit streams. The data must be divided into transmission blocks, to which the additional check data is added. The term usually applies to a single parity bit per bit stream, calculated independently of all the other bit streams ( BIP-8), : "Reliable link layer protocols". although it could also be used to refer to a larger Hamming code. This "extra" LRC word at the end of a block of data is very similar to checksum and cyclic redundancy check (CRC). Optimal rectangular code While simple longitudinal parity can only detect errors, it can be combined with additional error-control coding, such as a transverse redundancy check (TRC), to correct errors. The transverse redundancy check is stored on a dedicated "parity track". Whenever any single-bit error occurs in a transmission block of dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity Bit
A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits. The parity bit ensures that the total number of 1-bits in the string is even or odd. Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit's value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decoding Methods
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel. Notation C \subset \mathbb_2^n is considered a binary code with the length n; x,y shall be elements of \mathbb_2^n; and d(x,y) is the distance between those elements. Ideal observer decoding One may be given the message x \in \mathbb_2^n, then ideal observer decoding generates the codeword y \in C. The process results in this solution: :\mathbb(y \mbox \mid x \mbox) For example, a person can choose the codeword y that is most likely to be received as the message x after transmission. Decoding conventions Each codeword does not have an expected possibility: there may be more than one codeword with an equal likelihood of mutating into the received message. In such a case, the sender and receiver(s) mus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Code
In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of ''all'' block codes in a unified way. Such limitations often take the form of ''bounds'' that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors. Examples of block codes are Reed–Solomon codes, Hamming codes, Hadamard codes, Expander codes, Golay codes, and Reed–Muller codes. These examples also belong to the class of linear codes, and hence they are called linear block codes. More particularly, these codes are known as algebraic block codes, or cyclic block codes, because they can be generated using boolean polynomi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soft-decision Decoder
In information theory, a soft-decision decoder is a kind of decoding methods – a class of algorithm used to decode data that has been encoded with an error correcting code. Whereas a hard-decision decoder operates on data that take on a fixed set of possible values (typically 0 or 1 in a binary code), the inputs to a soft-decision decoder may take on a whole range of values in-between. This extra information indicates the reliability of each input data point, and is used to form better estimates of the original data. Therefore, a soft-decision decoder will typically perform better in the presence of corrupted data than its hard-decision counterpart. Soft-decision decoders are often used in Viterbi decoders and turbo code decoders. References See also * Forward error correction * Soft-in soft-out decoder A soft-in soft-out (SISO) decoder is a type of soft-decision decoder used with error correcting codes. "Soft-in" refers to the fact that the incoming data may take on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Detection And Correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases. Definitions ''Error detection'' is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver. ''Error correction'' is the detection of errors and reconstruction of the original, error-free data. History In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forward Error Correction
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Low-density Parity-check Code
In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel. An LDPC code is constructed using a sparse Tanner graph (subclass of the bipartite graph). LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum (the Shannon limit) for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length. LDPC codes are finding increasing use in applications requiring reliable and highly efficient information transfer over bandwidth-constrained or return-channel-constrained links in the presence of corrupting noise. Implementation of LDPC codes has lag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |