|
Mollweide Projection
file:Mollweide projection SW.jpg, 400px, Mollweide projection of the world file:Mollweide with Tissot's Indicatrices of Distortion.svg, 400px, The Mollweide projection with Tissot's indicatrix of deformation The Mollweide projection is an Equal-area map, equal-area, Map projection#Pseudocylindrical, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions. The projection was first published by mathematician and astronomer Karl Mollweide, Karl (or Carl) Brandan Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name homalographic projection. The variation homolographic arose from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mollweide Projection SW
Mollweide may refer to: *Karl Mollweide, mathematician (1774-1825). :*Mollweide projection, a pseudocylindrical map projection. :*Mollweide Glacier, a glacier the Victoria region of Antarctica. :*Mollweide's formula, a mathematical equation. {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goode Homolosine Projection
The Goode homolosine projection (or interrupted Goode homolosine projection) is a pseudocylindrical, equal-area, composite map projection used for world maps. Normally it is presented with multiple interruptions. Its equal-area property makes it useful for presenting spatial distribution of phenomena. Development The projection was developed in 1923 by John Paul Goode to provide an alternative to the Mercator projection for portraying global areal relationships. Goode offered variations of the interruption scheme for emphasizing the world’s land and the world’s oceans. Some variants include extensions that repeat regions in two different lobes of the interrupted map in order to show Greenland or eastern Russia undivided. The homolosine evolved from Goode’s 1916 experiments in interrupting the Mollweide projection. Because the Mollweide is sometimes called the "homolographic projection" (meaning, ''equal-area map''), Goode fused the two names " homolographic" and "sinusoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
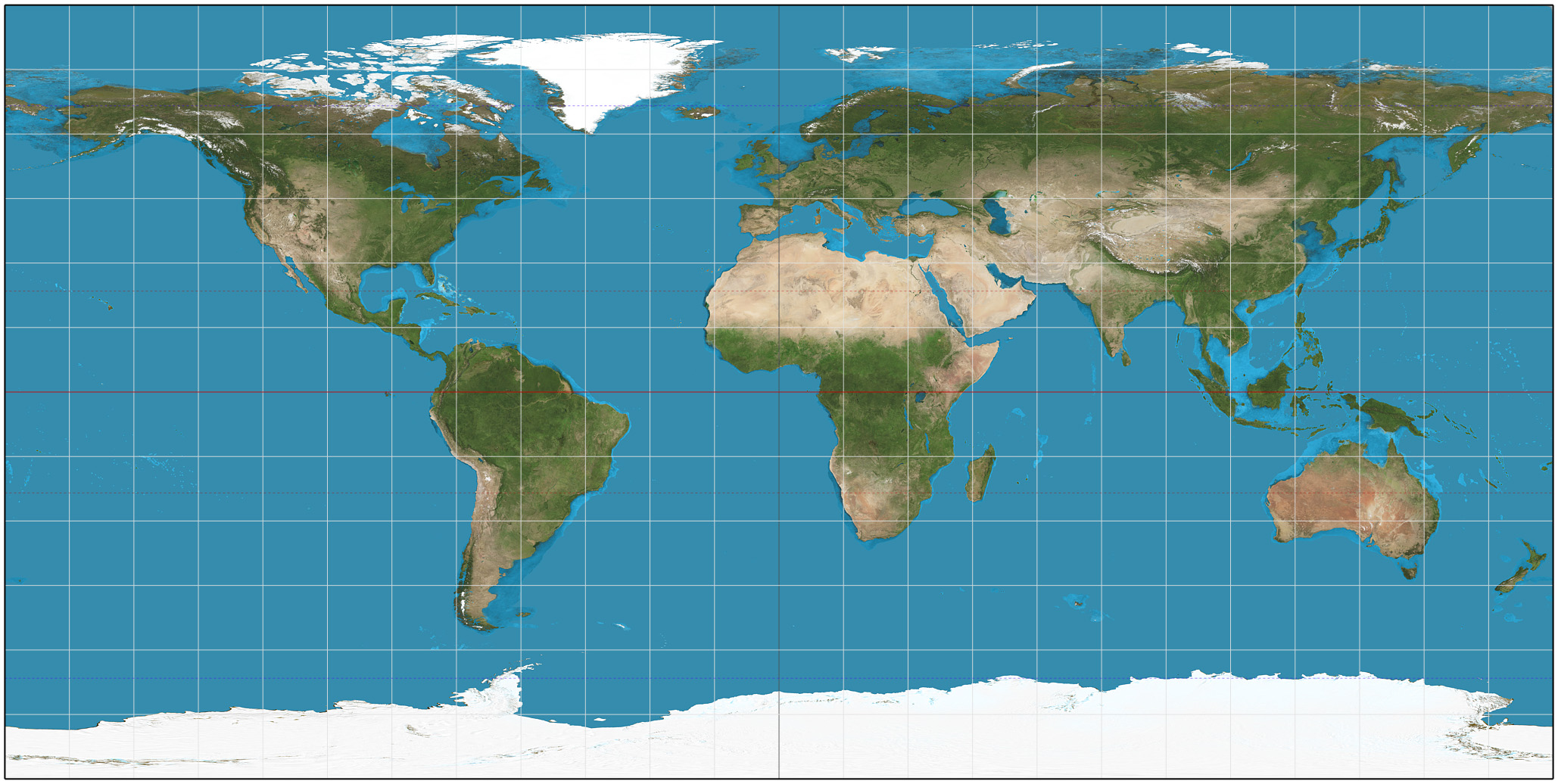
Tobler Hyperelliptical Projection
The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections that may be used for world maps. Waldo R. Tobler introduced the construction in 1973 as the ''hyperelliptical'' projection, now usually known as the Tobler hyperelliptical projection. Overview As with any pseudocylindrical projection, in the projection’s normal aspect, the parallels of latitude are parallel, straight lines. Their spacing is calculated to provide the equal-area property. The projection blends the cylindrical equal-area projection, which has straight, vertical meridians, with meridians that follow a particular kind of curve known as ''superellipses'' or '' Lamé curves'' or sometimes as ''hyperellipses''. A hyperellipse is described by x^k + y^k = \gamma^k, where \gamma and k are free parameters. Tobler's hyperelliptical projection is given as: :\begin &x = \lambda alpha + (1 - \alpha) \frac\\ \alpha &y = \sin \varphi + \frac \int_0^y (\gamma^k - y^k)^ \end where \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hammer Projection
The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide. Development Directly inspired by the Aitoff projection, Hammer suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection: :\begin x &= \operatorname_x\left(\frac, \varphi\right) \\ y &= \tfrac12 \operatorname_y\left(\frac, \varphi\right) \end where laea and laea are the ''x'' and ''y'' components of the equatorial Lambert azimuthal equal-area projection. Written out explicitly: :\begin x &= \frac \\ y &= \frac \end The inverse is calculated with the intermediate variable :z \equiv \sqrt The longitude and latitudes can then be calculated by :\begin \lambda &= 2 \arctan \frac \\ \varphi &= \arcsin zy \end where ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aitoff Projection
The Aitoff projection is a modified azimuthal map projection proposed by David A. Aitoff in 1889. Based on the equatorial form of the azimuthal equidistant projection, Aitoff first halves longitudes, then projects according to the azimuthal equidistant, and then stretches the result horizontally into a 2:1 ellipse to compensate for having halved the longitudes. Expressed simply: :x = 2 \operatorname_x\left(\frac, \varphi\right), \qquad y = \operatorname_y \left(\frac\lambda 2, \varphi \right) where azeq and azeq are the ''x'' and ''y'' components of the equatorial azimuthal equidistant projection. Written out explicitly, the projection is: :x = \frac, \qquad y = \frac where :\alpha = \arccos\left(\cos\varphi\cos\frac\right)\, and sinc ''α'' is the unnormalized sinc function with the discontinuity removed. In all of these formulas, ''λ'' is the longitude from the central meridian and ''φ'' is the latitude. Three years later, Ernst Hermann Heinrich Hammer suggested ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division By Zero
In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as \tfrac, where is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number that, when multiplied by , gives (assuming a \neq 0); thus, division by zero is undefined. Since any number multiplied by zero is zero, the expression \tfrac is also undefined; when it is the form of a limit, it is an indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to \tfrac is contained in Anglo-Irish philosopher George Berkeley's criticism of infinitesimal calculus in 1734 in '' The Analyst'' ("ghosts of departed quantities"). There are mathematical structures in which \tfrac is defined for some such as in the Riemann sphere (a model of the extended complex plane) and the Projectively extended real line; however, such structures do not satisfy e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a single-variable function defined for a real variable , the function's derivative , and an initial guess for a root of . If the function satisfies sufficient assumptions and the initial guess is close, then :x_ = x_0 - \frac is a better approximation of the root than . Geometrically, is the intersection of the -axis and the tangent of the graph of at : that is, the improved guess is the unique root of the linear approximation at the initial point. The process is repeated as :x_ = x_n - \frac until a sufficiently precise value is reached. This algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
United States Geological Survey
The United States Geological Survey (USGS), formerly simply known as the Geological Survey, is a scientific agency of the United States government. The scientists of the USGS study the landscape of the United States, its natural resources, and the natural hazards that threaten it. The organization's work spans the disciplines of biology, geography, geology, and hydrology. The USGS is a fact-finding research organization with no regulatory responsibility. The agency was founded on March 3, 1879. The USGS is a bureau of the United States Department of the Interior; it is that department's sole scientific agency. The USGS employs approximately 8,670 people and is headquartered in Reston, Virginia. The USGS also has major offices near Lakewood, Colorado, at the Denver Federal Center, and Menlo Park, California. The current motto of the USGS, in use since August 1997, is "science for a changing world". The agency's previous slogan, adopted on the occasion of its hundredth an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boggs Eumorphic Projection
The Boggs eumorphic projection is a pseudocylindrical, equal-area map projection used for world maps. Normally it is presented with multiple interruptions. Its equal-area property makes it useful for presenting spatial distribution of phenomena. The projection was developed in 1929 by Samuel Whittemore Boggs (1889–1954) to provide an alternative to the Mercator projection for portraying global areal relationships. Boggs was geographer for the United States Department of State from 1924 until his death. The Boggs eumorphic projection has been used occasionally in textbooks and atlases. Boggs generally repeated regions in two different lobes of the interrupted map in order to show Greenland or eastern Russia undivided. He preferred his interrupted version, and named it "eumorphic”, meaning "goodly shaped" (in Boggs's own words). The projection's mathematical development was completed by Oscar S. Adams of the U.S. Coast and Geodetic Survey. Formulas The projection averages ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |