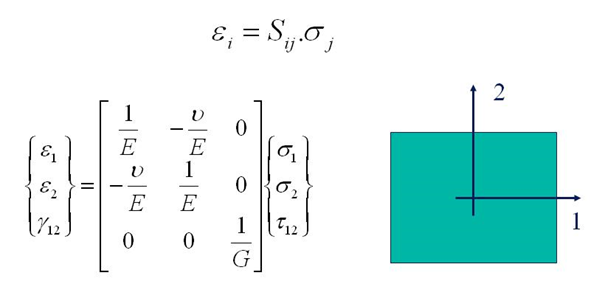|
Modulus Of Elasticity
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are: # ''Young's modulus'' (E) describes tensile and compressi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Of Measurement
A unit of measurement is a definite magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multiple of the unit of measurement. For example, a length is a physical quantity. The metre (symbol m) is a unit of length that represents a definite predetermined length. For instance, when referencing "10 metres" (or 10 m), what is actually meant is 10 times the definite predetermined length called "metre". The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to the present. A multitude of systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system. In trade, weights and measures is often a subject of governmental regulation, to ensure fairness and transparen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensile Strength
Ultimate tensile strength (UTS), often shortened to tensile strength (TS), ultimate strength, or F_\text within equations, is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials the ultimate tensile strength is close to the yield point, whereas in ductile materials the ultimate tensile strength can be higher. The ultimate tensile strength is usually found by performing a tensile test and recording the engineering stress versus strain. The highest point of the stress–strain curve is the ultimate tensile strength and has units of stress. The equivalent point for the case of compression, instead of tension, is called the compressive strength. Tensile strengths are rarely of any consequence in the design of ductile members, but they are important with brittle members. They are tabulated for common materials such as alloys, composite materials, ceramics, plastics, and wood. Definition The ultimate tensile ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Limit
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation. The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing permanent deformation. In some materials, such as aluminium, there is a gradual onset of non-linear behavior, making the precise yield point difficult to determine. In such a case, the offset y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impulse Excitation Technique
The impulse excitation technique (IET) is a non-destructive material characterization technique to determine the elastic properties and internal friction of a material of interest. It measures the resonant frequencies in order to calculate the Young's modulus, shear modulus, Poisson's ratio and internal friction of predefined shapes like rectangular bars, cylindrical rods and disc shaped samples. The measurements can be performed at room temperature or at elevated temperatures (up to 1700 °C) under different atmospheres. The measurement principle is based on tapping the sample with a small projectile and recording the induced vibration signal with a piezoelectric sensor, microphone, laser vibrometer or accelerometer. To optimize the results a microphone or a laser vibrometer can be used as there is no contact between the test-piece and the sensor. Laser vibrometers are preferred to measure signals in vacuum. Afterwards, the acquired vibration signal in the time domain is co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Modulus
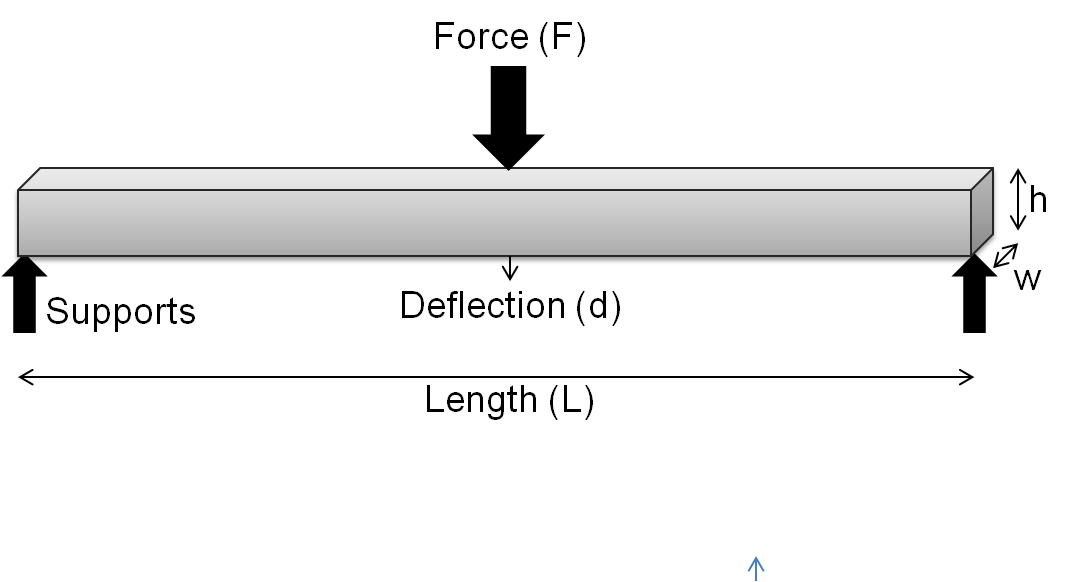
In mechanics, the flexural modulus or bending modulus is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D790), and uses units of force per area. The flexural modulus defined using the 2-point (cantilever) and 3-point bend tests assumes a linear stress strain response. For a 3-point test of a rectangular beam behaving as an isotropic linear material, where ''w'' and ''h'' are the width and height of the beam, ''I'' is the second moment of area of the beam's cross-section, ''L'' is the distance between the two outer supports, and ''d'' is the deflection due to the load ''F'' applied at the middle of the beam, the flexural modulus: : E_ = \frac From elastic beam theory :d = \frac and for rectangular beam : I = \fracwh^3 thus E_ = E ( Elastic modulus) For very small stra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Wave
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics. The fundamental "linearizing" assumptions of linear elasticity are: infinitesimal strains or "small" deformations (or strains) and linear relationships between the components of stress and strain. In addition linear elasticity is valid only for stress states that do not produce yielding. These assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis. Mathematical formulation Equations governing a linear elastic boundary value problem are based on three tensor partial differential equations for the balance of linear momentum and six infinitesimal strain-d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Limit
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation. The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing permanent deformation. In some materials, such as aluminium, there is a gradual onset of non-linear behavior, making the precise yield point difficult to determine. In such a case, the offset ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Modulus
Dynamic modulus (sometimes complex modulusThe Open University (UK), 2000. ''T838 Design and Manufacture with Polymers: Solid properties and design'', page 30. Milton Keynes: The Open University.) is the ratio of stress to strain under ''vibratory conditions'' (calculated from data obtained from either free or forced vibration tests, in shear, compression, or elongation). It is a property of viscoelastic materials. Viscoelastic stress–strain phase-lag Viscoelasticity is studied using dynamic mechanical analysis where an oscillatory force (stress) is applied to a material and the resulting displacement (strain) is measured. *In purely elastic materials the stress and strain occur in phase, so that the response of one occurs simultaneously with the other. *In purely viscous materials, there is a phase difference between stress and strain, where strain lags stress by a 90 degree (\pi/2 radian) phase lag. *Viscoelastic materials exhibit behavior somewhere in between that of pu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending Stiffness
The bending stiffness (K) is the resistance of a member against bending deformation. It is a function of the Young's modulus E, the second moment of area I of the beam cross-section about the axis of interest, length of the beam and beam boundary condition. Bending stiffness of a beam can analytically be derived from the equation of beam deflection when it is applied by a force. :K = \frac where \mathrm is the applied force and \mathrm is the deflection. According to elementary beam theory, the relationship between the applied bending moment M and the resulting curvature \kappa of the beam is: :M = E I \kappa = E I \frac{\mathrm{d} x^2} where w is the deflection of the beam and x is the distance along the beam. Double integration of the above equation leads to computing the deflection of the beam, and in turn, the bending stiffness of the beam. Bending stiffness in beams is also known as Flexural rigidity. See also * Applied mechanics * Beam theory * Bending *Stiffness Stiffne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |