|
Modulation Transfer Function (infrared Imaging)
The optical transfer function (OTF) of an optical system such as a camera, microscope, human eye, or image projector, projector is a scale-dependent description of their imaging contrast. Its magnitude is the image contrast of the Sine and cosine, harmonic intensity pattern, 1 + \cos(2\pi \nu \cdot x), as a function of the spatial frequency, \nu, while its Argument (complex analysis), complex argument indicates a phase shift in the periodic pattern. The optical transfer function is used by optical engineers to describe how the optics project light from the object or scene onto a photographic film, Image sensor, detector array, retina, screen, or simply the next item in the optical transmission chain. Formally, the optical transfer function is defined as the Fourier transform of the point spread function (PSF, that is, the impulse response of the optics, the image of a point source). As a Fourier transform, the OTF is generally complex-valued; however, it is real-valued in the comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
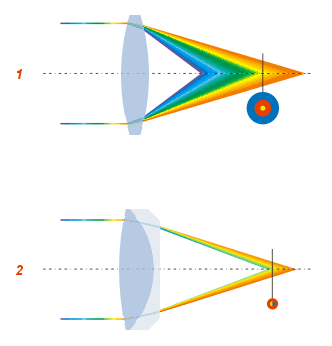
Illustration Of The Optical Transfer Function And Its Relation To Image Quality
An illustration is a decoration, interpretation, or visual explanation of a text, concept, or process, designed for integration in print and digitally published media, such as posters, flyers, magazines, books, teaching materials, animations, video games and films. An illustration is typically created by an illustrator. Digital illustrations are often used to make websites and apps more user-friendly, such as the use of emojis to accompany digital type. Illustration also means providing an example; either in writing or in picture form. The origin of the word "illustration" is late Middle English (in the sense ‘illumination; spiritual or intellectual enlightenment’): via Old French from Latin">-4; we might wonder whether there's a point at which it's appropriate to talk of the beginnings of French, that is, when it wa ... from Latin ''illustratio''(n-), from the verb ''illustrare''. Illustration styles Contemporary illustration uses a wide range of styles and techniqu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Resolution
Optical resolution describes the ability of an imaging system to resolve detail, in the object that is being imaged. An imaging system may have many individual components, including one or more lenses, and/or recording and display components. Each of these contributes (given suitable design, and adequate alignment) to the optical resolution of the system; the environment in which the imaging is done often is a further important factor. Lateral resolution Resolution depends on the distance between two distinguishable radiating points. The sections below describe the theoretical estimates of resolution, but the real values may differ. The results below are based on mathematical models of Airy discs, which assumes an adequate level of contrast. In low-contrast systems, the resolution may be much lower than predicted by the theory outlined below. Real optical systems are complex, and practical difficulties often increase the distance between distinguishable point sources. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zernike Polynomials
In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike, laureate of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy, they play important roles in various optics branches such as beam optics and imaging. Definitions There are even and odd Zernike polynomials. The even Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\cos(m\,\varphi) \! (even function over the azimuthal angle \varphi), and the odd Zernike polynomials are defined as :Z^_n(\rho,\varphi) = R^m_n(\rho)\,\sin(m\,\varphi), \! (odd function over the azimuthal angle \varphi) where ''m'' and ''n'' are nonnegative integers with ''n ≥ m ≥ 0'' (''m'' = 0 for spherical Zernike polynomials), ''\varphi'' is the azimuthal angle, ''ρ'' is the radial distance 0\le\rho\le 1, and R^m_n are the radial polynomials defined below. Zernike polynomials have the property of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Aberrations
In optics, aberration is a property of optical systems, such as lenses and mirrors, that causes the ''image'' created by the optical system to not be a faithful reproduction of the ''object'' being observed. Aberrations cause the image formed by a lens to be blurred, distorted in shape or have color fringing or other effects not seen in the object, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which is not sharp. M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trefoil Aberration PSF OTF And Example Image
A trefoil () is a graphic form composed of the outline of three overlapping rings, used in architecture, Pagan and Christian symbolism, among other areas. The term is also applied to other symbols with a threefold shape. A similar shape with four rings is called a quatrefoil. Architecture Ornamentation 'Trefoil' is a term in Gothic architecture given to the ornamental foliation or cusping introduced in the heads of window-lights, tracery, and panellings, in which the centre takes the form of a three-lobed leaf (formed from three partially overlapping circles). One of the earliest examples is in the plate tracery at Winchester Cathedral (1222–1235). The fourfold version of an architectural trefoil is a quatrefoil. A simple trefoil shape in itself can be symbolic of the Trinity, while a trefoil combined with an equilateral triangle was also a moderately common symbol of the Christian Trinity during the late Middle Ages in some parts of Europe, similar to a barbed quatrefoil. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aliasing
In signal processing and related disciplines, aliasing is a phenomenon that a reconstructed signal from samples of the original signal contains low frequency components that are not present in the original one. This is caused when, in the original signal, there are components at frequency exceeding a certain frequency called Nyquist frequency, f_s / 2, where f_s is the sampling frequency ( undersampling). This is because typical reconstruction methods use low frequency components while there are a number of frequency components, called aliases, which sampling result in the identical sample. It also often refers to the distortion or artifact that results when a signal reconstructed from samples is different from the original continuous signal. Aliasing can occur in signals sampled in time, for instance in digital audio or the stroboscopic effect, and is referred to as temporal aliasing. Aliasing in spatially sampled signals (e.g., moiré patterns in digital images) is referre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist–Shannon Sampling Theorem
The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate required to avoid a type of distortion called aliasing. The theorem states that the sample rate must be at least twice the Bandwidth (signal processing), bandwidth of the signal to avoid aliasing. In practice, it is used to select band-limiting filters to keep aliasing below an acceptable amount when an analog signal is sampled or when sample rates are changed within a digital signal processing function. The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of ''samples'' to capture all the information from a continuous-time signal of finite Bandwidth (signal processing), bandwidth. Strictly speaking, the theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-number
An f-number is a measure of the light-gathering ability of an optical system such as a camera lens. It is calculated by dividing the system's focal length by the diameter of the entrance pupil ("clear aperture").Smith, Warren ''Modern Optical Engineering'', 4th Ed., 2007 McGraw-Hill Professional, p. 183. The f-number is also known as the focal ratio, f-ratio, or f-stop, and it is key in determining the depth of field, diffraction, and Exposure (photography), exposure of a photograph. The f-number is dimensionless number, dimensionless and is usually expressed using a lower-case Ƒ, hooked f with the format ''N'', where ''N'' is the f-number. The f-number is also known as the inverse relative aperture, because it is the Multiplicative inverse, inverse of the relative aperture, defined as the aperture diameter divided by focal length. The relative aperture indicates how much light can pass through the lens at a given focal length. A lower f-number means a larger relative apertur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Aberration
In optics, aberration is a property of optical systems, such as Lens (optics), lenses and mirrors, that causes the ''image'' created by the optical system to not be a faithful reproduction of the ''object'' being observed. Aberrations cause the image formed by a lens to be blurred, distorted in shape or have color fringing or other effects not seen in the object, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible input. It is widely used in electronic engineering tools like Electronic circuit simulation, circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph (function), graph of an independent scalar (mathematics), scalar input versus the dependent scalar output (known as a transfer curve or characteristic curve). Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. Dimensions and units of the transfer function model the output response of the device for a range of possible inputs. The transfer function of a two-port electronic circuit, such as an amplifier, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if it is either entirely non-decreasing, or entirely non-increasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is termed ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\right), so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |