|
Mittag-Leffler Function
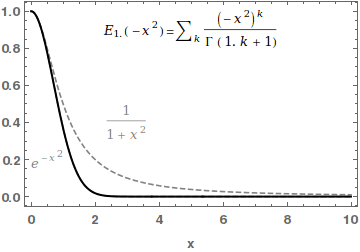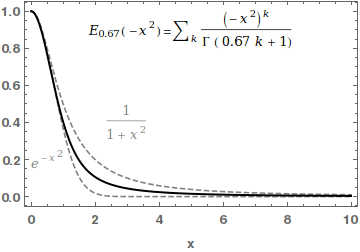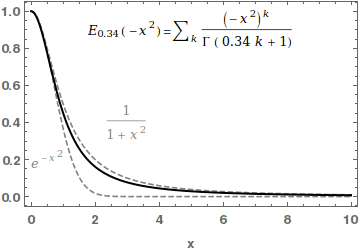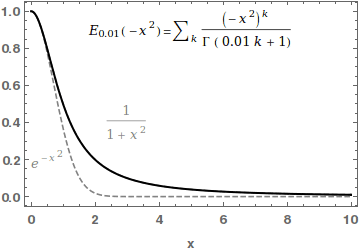
In mathematics, the Mittag-Leffler function E_ is a special function, a complex function which depends on two complex parameters \alpha and \beta. It may be defined by the following series when the real part of \alpha is strictly positive: :E_ (z) = \sum_^\infty \frac, where \Gamma(x) is the gamma function. When \beta=1, it is abbreviated as E_\alpha(z) = E_(z). For \alpha=0, the series above equals the Taylor expansion of the geometric series and consequently E_(z)=\frac\frac. In the case \alpha and \beta are real and positive, the series converges for all values of the argument z, so the Mittag-Leffler function is an entire function. This function is named after Gösta Mittag-Leffler. This class of functions are important in the theory of the fractional calculus. For \alpha >0 , the Mittag-Leffler function E_(z) is an entire function of order 1/\alpha, and is in some sense the simplest entire function of its order. The Mittag-Leffler function satisfies the recurrence prope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the ''common ratio''. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. Examples of a geometric sequence are powers ''r''''k'' of a fixed non-zero number ''r'', such as 2''k'' and 3''k''. The general form of a geometric sequence is :a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots where ''r'' ≠ 0 is the common ratio and ''a'' ≠ 0 is a scale factor, equal to the sequence's start value. The sum of a geometric progression terms is called a ''geometric series''. Elementary properties The ''n''-th term of a geometric sequence with initial value ''a'' = ''a''1 and common ratio ''r'' is given by :a_n = a\,r^, and in general :a_n = a_m\,r^. Such a geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fox–Wright Function
In mathematics, the Fox–Wright function (also known as Fox–Wright Psi function, not to be confused with Wright Omega function) is a generalisation of the generalised hypergeometric function ''p''''F''''q''(''z'') based on ideas of and : _p\Psi_q \left begin ( a_1 , A_1 ) & ( a_2 , A_2 ) & \ldots & ( a_p , A_p ) \\ ( b_1 , B_1 ) & ( b_2 , B_2 ) & \ldots & ( b_q , B_q ) \end ; z \right= \sum_^\infty \frac \, \frac . Upon changing the normalisation _p\Psi^*_q \left begin ( a_1 , A_1 ) & ( a_2 , A_2 ) & \ldots & ( a_p , A_p ) \\ ( b_1 , B_1 ) & ( b_2 , B_2 ) & \ldots & ( b_q , B_q ) \end ; z \right= \frac \sum_^\infty \frac \, \frac it becomes ''p''''F''''q''(''z'') for ''A''1...''p'' = B1...''q'' = 1. The Fox–Wright function is a special case of the Fox H-function : _p\Psi_q \left begin ( a_1 , A_1 ) & ( a_2 , A_2 ) & \ldots & ( a_p , A_p ) \\ ( b_1 , B_1 ) & ( b_2 , B_2 ) & \ldots & ( b_q , B_q ) \end ; z \right= H^_ \left \begin ( 1-a_1 , A_1 ) & ( 1-a_2 , A_2 ) & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mittag-Leffler Distribution
The Mittag-Leffler distributions are two families of probability distributions on the half-line ,\infty). They are parametrized by a real \alpha \in (0, 1/math> or \alpha \in , 1/math>. Both are defined with the Mittag-Leffler function, named after Gösta Mittag-Leffler. The Mittag-Leffler function For any complex \alpha whose real part is positive, the series :E_\alpha (z) := \sum_^\infty \frac defines an entire function. For \alpha = 0, the series converges only on a disc of radius one, but it can be analytically extended to \mathbb \setminus \. First family of Mittag-Leffler distributions The first family of Mittag-Leffler distributions is defined by a relation between the Mittag-Leffler function and their cumulative distribution functions. For all \alpha \in (0, 1], the function E_\alpha is increasing on the real line, converges to 0 in - \infty, and E_\alpha (0) = 1. Hence, the function x \mapsto 1-E_\alpha (-x^\alpha) is the cumulative distribution function of a probabi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscoelasticity
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed. Viscoelastic materials have elements of both of these properties and, as such, exhibit time-dependent strain. Whereas elasticity is usually the result of bond stretching along crystallographic planes in an ordered solid, viscosity is the result of the diffusion of atoms or molecules inside an amorphous material.Meyers and Chawla (1999): "Mechanical Behavior of Materials", 98-103. Background In the nineteenth century, physicists such as Maxwell, Boltzmann, and Kelvin researched and experimented with creep and recovery of glasses, metals, and rubbers. Viscoelasticity was further examined in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mittag-Leffler Summation
In mathematics, Mittag-Leffler summation is any of several variations of the Borel summation method for summing possibly divergent formal power series, introduced by Definition Let :y(z) = \sum_^\infty y_kz^k be a formal power series in ''z''. Define the transform \scriptstyle \mathcal_\alpha y of \scriptstyle y by :\mathcal_\alpha y(t) \equiv \sum_^\infty \fract^k Then the Mittag-Leffler sum of ''y'' is given by :\lim_\mathcal_\alpha y( z) if each sum converges and the limit exists. A closely related summation method, also called Mittag-Leffler summation, is given as follows . Suppose that the Borel transform \mathcal_1 y(z) converges to an analytic function near 0 that can be analytically continued along the positive real axis to a function growing sufficiently slowly that the following integral is well defined (as an improper integral). Then the Mittag-Leffler sum of ''y'' is given by :\int_0^\infty e^ \mathcal_\alpha y(t^\alpha z) \, dt When ''α'' = 1 this i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in ... that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex frequency domain, also known as ''s''-domain, or s-plane). The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions ''f'', the Laplace transform is the integral \mathcal\(s) = \int_0^\infty f(t)e^ \, dt. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Cosine
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 328 from which are derived: * hyperbolic tangent "" (), * hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a complex function of a complex variable defined as: :\operatorname z = \frac\int_0^z e^\,\mathrm dt. This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real. In statistics, for non-negative values of , the error function has the following interpretation: for a random variable that is normally distributed with mean 0 and standard deviation , is the probability that falls in the range . Two closely related functions are the complementary error function () defined as :\operatorname z = 1 - \operatorname z, and the imaginary error function () defined as :\operatorname z = -i\operatorname iz, where is the imaginary unit Name The name "error function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
