|
Misconceptions About The Normal Distribution
Students of statistics and probability theory sometimes develop misconceptions about the normal distribution, ideas that may seem plausible but are mathematically untrue. For example, it is sometimes mistakenly thought that two Pearson product-moment correlation coefficient, linearly uncorrelated, normal distribution, normally distributed random variables must be statistical independence, statistically independent. However, this is untrue, as can be demonstrated by counterexample. Likewise, it is sometimes mistakenly thought that a linear combination of normally distributed random variables will itself be normally distributed, but again, counterexamples prove this wrong. To say that the pair (X,Y) of random variables has a Multivariate normal distribution, bivariate normal distribution means that every linear combination aX+bY of X and Y for constant (i.e. not random) coefficients a and b (not both equal to zero) has a univariate normal distribution. In that case, if X and Y are unc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
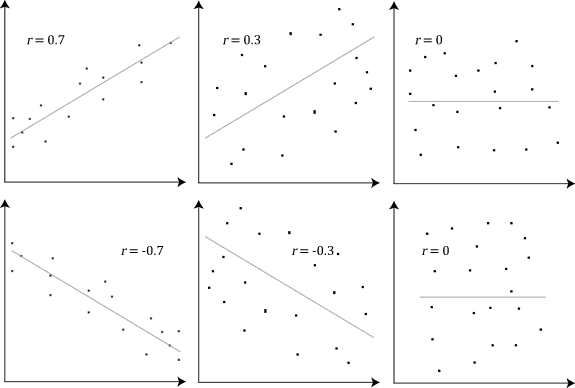
Covariance And Correlation
In probability theory and statistics, the mathematical concepts of covariance and correlation are very similar. Both describe the degree to which two random variables or sets of random variables tend to deviate from their expected values in similar ways. If ''X'' and ''Y'' are two random variables, with means (expected values) ''μX'' and ''μY'' and standard deviations ''σX'' and ''σY'', respectively, then their covariance and correlation are as follows: ; covariance :\text_ = \sigma_ = E X-\mu_X)\,(Y-\mu_Y)/math> ; correlation :\text_ = \rho_ = E X-\mu_X)\,(Y-\mu_Y)(\sigma_X \sigma_Y)\,, so that \rho_ = \sigma_ / (\sigma_X \sigma_Y) where ''E'' is the expected value operator. Notably, correlation is dimensionless while covariance is in units obtained by multiplying the units of the two variables. If ''Y'' always takes on the same values as ''X'', we have the covariance of a variable with itself (i.e. \sigma_), which is called the variance and is more commonly denoted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Probability Distributions
A theory is a systematic and rational form of abstract thinking about a phenomenon, or the conclusions derived from such thinking. It involves contemplative and logical reasoning, often supported by processes such as observation, experimentation, and research. Theories can be scientific, falling within the realm of empirical and testable knowledge, or they may belong to non-scientific disciplines, such as philosophy, art, or sociology. In some cases, theories may exist independently of any formal discipline. In modern science, the term "theory" refers to scientific theories, a well-confirmed type of explanation of nature, made in a way consistent with the scientific method, and fulfilling the criteria required by modern science. Such theories are described in such a way that scientific tests should be able to provide empirical support for it, or empirical contradiction (" falsify") of it. Scientific theories are the most reliable, rigorous, and comprehensive form of scientific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation And Dependence
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Marginals
Normal(s) or The Normal(s) may refer to: Film and television * ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson * ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum Keith Rennie, and Andrew Airlie * ''Normal'' (2009 film), an adaptation of Anthony Neilson's 1991 play ''Normal: The Düsseldorf Ripper'' * '' Normal!'', a 2011 Algerian film * ''The Normals'' (film), a 2012 American comedy film * "Normal" (''New Girl''), an episode of the TV series Mathematics * Normal (geometry), an object such as a line or vector that is perpendicular to a given object * Normal basis (of a Galois extension), used heavily in cryptography * Normal bundle * Normal cone, of a subscheme in algebraic geometry * Normal coordinates, in differential geometry, local coordinates obtained from the exponential map (Riemannian geometry) * Normal distribution, the Gaussian continuous probability distribution * Normal equations, describing the solution of the linear least s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the \chi^2-distribution with k Degrees of freedom (statistics), degrees of freedom is the distribution of a sum of the squares of k Independence (probability theory), independent standard normal random variables. The chi-squared distribution \chi^2_k is a special case of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim \chi^2_k then X \sim \text(\alpha=\frac, \theta=2) (where \alpha is the shape parameter and \theta the scale parameter of the gamma distribution) and X \sim \text_1(1,k) . The scaled chi-squared distribution s^2 \chi^2_k is a reparametrization of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim s^2 \chi^2_k then X \sim \text(\alpha=\frac, \theta=2 s^2) and X \sim \text_1(s^2,k) . The chi-squared distribution is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in constru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Distribution
The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f(x; x_0,\gamma) is the distribution of the -intercept of a ray issuing from (x_0,\gamma) with a uniformly distributed angle. It is also the distribution of the Ratio distribution, ratio of two independent Normal distribution, normally distributed random variables with mean zero. The Cauchy distribution is often used in statistics as the canonical example of a "pathological (mathematics), pathological" distribution since both its expected value and its variance are undefined (but see below). The Cauchy distribution does not have finite moment (mathematics), moments of order greater than or equal to one; only fractional absolute moments exist., Chapter 16. The Cauchy dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The American Statistician
''The American Statistician'' is a quarterly peer-reviewed scientific journal covering statistics published by Taylor & Francis on behalf of the American Statistical Association. It was established in 1947. The editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The editor-in-chief heads all departments of the organization and is held accoun ... is Daniel R. Jeske, a professor at the University of California, Riverside. External links * Taylor & Francis academic journals Statistics journals Academic journals established in 1947 English-language journals Quarterly journals 1947 establishments in the United States Academic journals associated with learned and professional societies of the United States {{statistics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermediate Value Theorem
In mathematical analysis, the intermediate value theorem states that if f is a continuous function whose domain contains the interval , then it takes on any given value between f(a) and f(b) at some point within the interval. This has two important corollaries: # If a continuous function has values of opposite sign inside an interval, then it has a root in that interval (Bolzano's theorem). # The image of a continuous function over an interval is itself an interval. Motivation This captures an intuitive property of continuous functions over the real numbers: given ''f'' continuous on ,2/math> with the known values f(1) = 3 and f(2) = 5, then the graph of y = f(x) must pass through the horizontal line y = 4 while x moves from 1 to 2. It represents the idea that the graph of a continuous function on a closed interval can be drawn without lifting a pencil from the paper. Theorem The intermediate value theorem states the following: Consider the closed interval I = ,b/math> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |