|
Milin's Area Theorem
In complex analysis and geometric function theory, the Grunsky matrices, or Grunsky operators, are infinite matrices introduced in 1939 by Helmut Grunsky. The matrices correspond to either a single holomorphic function on the unit disk or a pair of holomorphic functions on the unit disk and its complement. The Grunsky inequalities express boundedness properties of these matrices, which in general are contraction operators or in important special cases unitary operators. As Grunsky showed, these inequalities hold if and only if the holomorphic function is univalent. The inequalities are equivalent to the inequalities of Goluzin, discovered in 1947. Roughly speaking, the Grunsky inequalities give information on the coefficients of the logarithm of a univalent function; later generalizations by Milin, starting from the Lebedev–Milin inequality, succeeded in exponentiating the inequalities to obtain inequalities for the coefficients of the univalent function itself. The Grunsky matri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical branches in mathematics, with roots in the 18th century and just prior. Important mathematicians associated with comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Field Theory
A conformal field theory (CFT) is a quantum field theory that is invariant under conformal transformations. In two dimensions, there is an infinite-dimensional algebra of local conformal transformations, and conformal field theories can sometimes be exactly solved or classified. Conformal field theory has important applications to condensed matter physics, statistical mechanics, quantum statistical mechanics, and string theory. Statistical and condensed matter systems are indeed often conformally invariant at their thermodynamic or quantum critical points. Scale invariance vs conformal invariance In quantum field theory, scale invariance is a common and natural symmetry, because any fixed point of the renormalization group is by definition scale invariant. Conformal symmetry is stronger than scale invariance, and one needs additional assumptions to argue that it should appear in nature. The basic idea behind its plausibility is that ''local'' scale invariant theories have t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Value Integral
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined. Formulation Depending on the type of singularity in the integrand , the Cauchy principal value is defined according to the following rules: In some cases it is necessary to deal simultaneously with singularities both at a finite number and at infinity. This is usually done by a limit of the form \lim_\, \lim_ \,\left ,\int_^ f(x)\,\mathrmx \,~ + ~ \int_^ f(x)\,\mathrmx \,\right In those cases where the integral may be split into two independent, finite limits, \lim_ \, \left, \,\int_a^ f(x)\,\mathrmx \,\\; < \;\infty and then the function is integrable in the ordinary sense. The result of the procedure for principal value is the same as the ordinary integral; since it no longer matches the definition, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Louis De Branges
Louis de Branges de Bourcia (born August 21, 1932) is a French-American mathematician. He is the Edward C. Elliott Distinguished Professor of Mathematics at Purdue University in West Lafayette, Indiana. He is best known for proving the long-standing Bieberbach conjecture in 1984, now called de Branges's theorem. He claims to have proved several important conjectures in mathematics, including the generalized Riemann hypothesis. Born to American parents who lived in Paris, de Branges moved to the US in 1941 with his mother and sisters. His native language is French. He did his undergraduate studies at the Massachusetts Institute of Technology (1949–53), and received a PhD in mathematics from Cornell University (1953–57). His advisors were Wolfgang Fuchs and then-future Purdue colleague Harry Pollard. He spent two years (1959–60) at the Institute for Advanced Study and another two (1961–62) at the Courant Institute of Mathematical Sciences. He was appointed to Purdue in 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gronwall's Area Theorem
In complex analysis, a branch of mathematics, the Koebe 1/4 theorem states the following: Koebe Quarter Theorem. The image of an injective analytic function f:\mathbf\to\mathbb from the unit disk \mathbf onto a subset of the complex plane contains the disk whose center is f(0) and whose radius is , f'(0), /4. The theorem is named after Paul Koebe, who conjectured the result in 1907. The theorem was proven by Ludwig Bieberbach in 1916. The example of the Koebe function shows that the constant 1/4 in the theorem cannot be improved (increased). A related result is the Schwarz lemma, and a notion related to both is conformal radius. Grönwall's area theorem Suppose that :g(z) = z +b_1z^ + b_2 z^ + \cdots is univalent in , z, >1. Then :\sum_ n, b_n, ^2 \le 1. In fact, if r > 1, the complement of the image of the disk , z, >r is a bounded domain X(r). Its area is given by : \int_ dx\,dy = \int_\overline\,dz = \int_\overline\,dg=\pi r^2 - \pi\sum n, b_n, ^2 r^. Since the ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reproducing Kernel
In functional analysis (a branch of mathematics), a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Roughly speaking, this means that if two functions f and g in the RKHS are close in norm, i.e., \, f-g\, is small, then f and g are also pointwise close, i.e., , f(x)-g(x), is small for all x. The converse does not need to be true. Informally, this can be shown by looking at the supremum norm: the sequence of functions \sin^n (x) converges pointwise, but do not converge uniformly i.e. do not converge with respect to the supremum norm (note that this is not a counterexample because the supremum norm does not arise from any inner product due to not satisfying the parallelogram law). It is not entirely straightforward to construct a Hilbert space of functions which is not an RKHS. Some examples, however, have been found. Note that ''L''2 spaces are not Hilbert spaces of functions (and hence not RKH ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
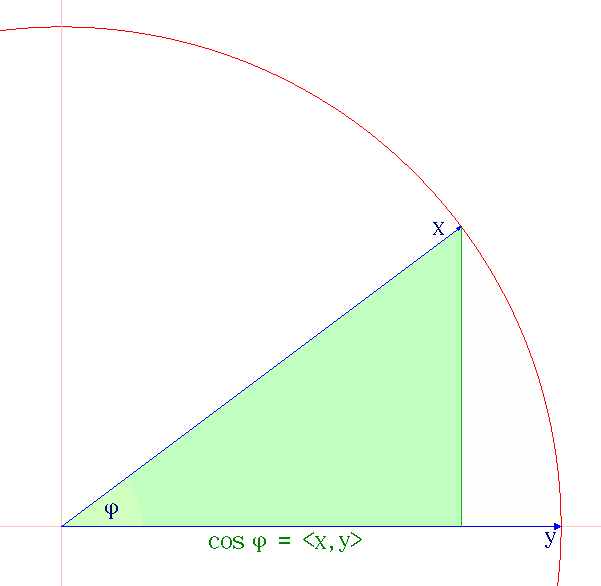
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue Measure
In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of ''n''-dimensional Euclidean space. For ''n'' = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called ''n''-dimensional volume, ''n''-volume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set ''A'' is here denoted by ''λ''(''A''). Henri Lebesgue described this measure in the year 1901, followed the next year by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902. Definition For any interval I = ,b/math>, or I = (a, b), in the set \mathbb of real numbers, let \ell(I)= b - a denote its length. For any subset E\subseteq\mathbb, the Lebesg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential 1-form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics. For instance, the expression is an example of a -form, and can be integrated over an interval contained in the domain of : :\int_a^b f(x)\,dx. Similarly, the expression is a -form that can be integrated over a surface : :\int_S (f(x,y,z)\,dx\wedge dy + g(x,y,z)\,dz\wedge dx + h(x,y,z)\,dy\wedge dz). The symbol denotes the exterior product, sometimes called the ''wedge product'', of two differential forms. Likewise, a -form represents a volume element that can be integrated over a region of space. In general, a -form is an object that may be integrated over a -dimensional manifold, and is homogeneous of degree in the coordinate differentials dx, dy, \ldots. On an -dimensional manifold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |