|
Mild-slope Equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts. The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliffs, beaches, seawalls and breakwaters. As a result, it describes the variations in wave amplitude, or equivalently wave height. From the wave amplitude, the amplitude of the flow velocity oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to determ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
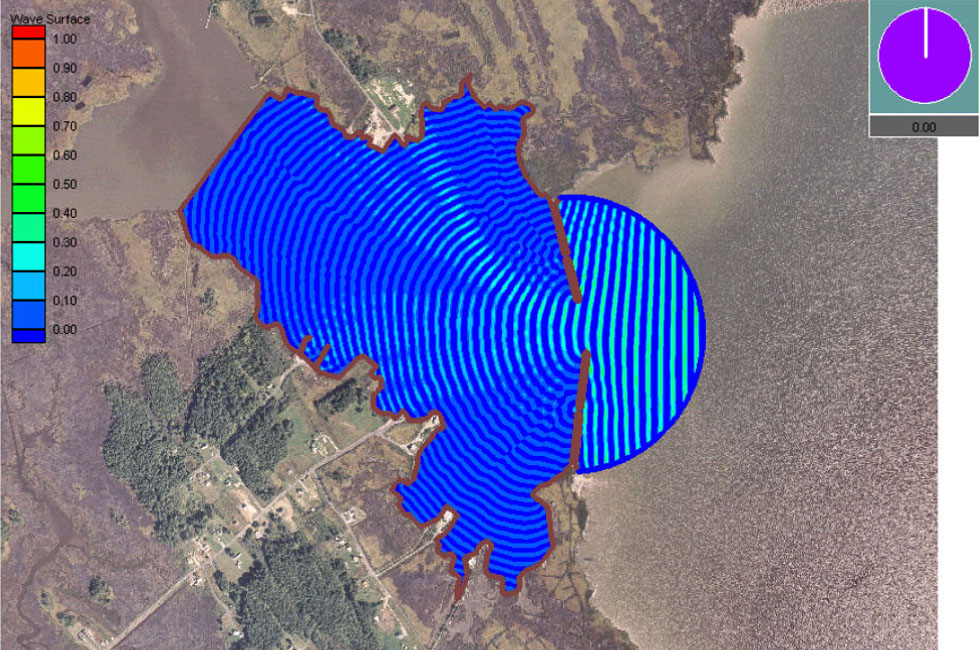
CGWAVE Tedious Creek MD
SMS (Surface-water Modeling System) is a complete program for building and simulating surface water models from Aquaveo. It features 1D and 2D modeling and a unique conceptual model approach. Currently supported models include ADCIRC, CMS-FLOW2D, FESWMS, TABS, TUFLOW, BOUSS-2D, CGWAVE, STWAVE, CMS-WAVE (WABED), GENESIS, PTM, and WAM. Version 9.2 introduced the use of XMDF (eXtensible Model Data Format), which is a compatible extension of HDF5. XMDF files are smaller and allow faster access times than ASCII files. History SMS was initially developed by the ''Engineering Computer Graphics Laboratory'' at Brigham Young University (later renamed in September, 1998 to ''Environmental Modeling Research Laboratory'' or EMRL) in the late 1980s on Unix workstations. The development of SMS was funded primarily by The United States Army Corps of Engineers and is still known as the ''Department of Defense Surface-water Modeling System'' or ''DoD SMS''. It was later ported to Windows platfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sediment Transport
Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems where the particles are clastic rocks (sand, gravel, boulders, etc.), mud, or clay; the fluid is air, water, or ice; and the force of gravity acts to move the particles along the sloping surface on which they are resting. Sediment transport due to fluid motion occurs in rivers, oceans, lakes, seas, and other bodies of water due to currents and tides. Transport is also caused by glaciers as they flow, and on terrestrial surfaces under the influence of wind. Sediment transport due only to gravity can occur on sloping surfaces in general, including hillslopes, scarps, cliffs, and the continental shelf—continental slope boundary. Sediment transport is important in the fields of sedimentary geology, geomorphology, civil engineering, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress, such as the interface between two homogeneous fluids. An example of two such homogeneous fluids would be a body of water (liquid) and the air in the Earth's atmosphere (gas mixture). Unlike liquids, gases cannot form a free surface on their own. Fluidized/liquified solids, including slurries, granular materials, and powders may form a free surface. A liquid in a gravitational field will form a free surface if unconfined from above. Under mechanical equilibrium this free surface must be perpendicular to the forces acting on the liquid; if not there would be a force along the surface, and the liquid would flow in that direction. Thus, on the surface of the Earth, all free surfaces of liquids are horizontal unless disturbed (except near solids dipping into them, where surface tension distorts the surface in a region called the meniscus). In a free liquid that is not affected by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Airy Wave Theory
In fluid dynamics, Airy wave theory (often referred to as linear wave theory) gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.Craik (2004). Airy wave theory is often applied in ocean engineering and coastal engineering for the modelling of random sea states – giving a description of the wave kinematics and dynamics of high-enough accuracy for many purposes. Further, several second-order nonlinear properties of surface gravity waves, and their propagation, can be estimated from its results. Airy wave theory is also a good approximation for tsunami waves in the ocean, before they steepen near the coast. This linear theory is often used to get a quick and rough estimate of wave characterist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monochromatic
A monochrome or monochromatic image, object or color scheme, palette is composed of one color (or lightness, values of one color). Images using only Tint, shade and tone, shades of grey are called grayscale (typically digital) or Black and white, black-and-white (typically analog). In physics, Monochromatic radiation, monochromatic light refers to electromagnetic radiation that contains a narrow band of wavelengths, which is a distinct concept. Application Of an image, the term monochrome is usually taken to mean the same as black and white or, more likely, grayscale, but may also be used to refer to other combinations containing only tones of a single color, such as green-and-white or green-and-red. It may also refer to Sepia tone, sepia displaying tones from light tan to dark brown or cyanotype ("blueprint") images, and early photographic methods such as daguerreotypes, ambrotypes, and tintypes, each of which may be used to produce a monochromatic image. In computing, monoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Equation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation \nabla^2 f = -k^2 f, where is the Laplace operator (or "Laplacian"), is the eigenvalue, and is the (eigen)function. When the equation is applied to waves, is known as the wave number. The Helmholtz equation has a variety of applications in physics, including the wave equation and the diffusion equation, and it has uses in other sciences. Motivation and uses The Helmholtz equation often arises in the study of physical problems involving partial differential equations (PDEs) in both space and time. The Helmholtz equation, which represents a time-independent form of the wave equation, results from applying the technique of separation of variables to reduce the complexity of the analysis. For example, consider the wave equation \left(\nabla^2-\frac\frac\right) u(\mathbf,t)=0. Separation of variables begins by assumi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabolic Partial Differential Equation
A parabolic partial differential equation is a type of partial differential equation (PDE). Parabolic PDEs are used to describe a wide variety of time-dependent phenomena, including heat conduction, particle diffusion, and pricing of derivative investment instruments. Definition To define the simplest kind of parabolic PDE, consider a real-valued function u(x, y) of two independent real variables, x and y. A second-order, linear, constant-coefficient PDE for u takes the form :Au_ + 2Bu_ + Cu_ + Du_x + Eu_y + F = 0, and this PDE is classified as being ''parabolic'' if the coefficients satisfy the condition :B^2 - AC = 0. Usually x represents one-dimensional position and y represents time, and the PDE is solved subject to prescribed initial and boundary conditions. The name "parabolic" is used because the assumption on the coefficients is the same as the condition for the analytic geometry equation A x^2 + 2B xy + C y^2 + D x + E y + F = 0 to define a planar parabola. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Breaking
In fluid dynamics, a breaking wave or breaker is a wave whose amplitude reaches a critical level at which large amounts of wave energy transform into turbulent kinetic energy. At this point, simple physical models that describe wave dynamics often become invalid, particularly those that assume linear behaviour. The most generally familiar sort of breaking wave is the breaking of water surface waves on a coastline. Wave breaking generally occurs where the amplitude reaches the point that the crest of the wave actually overturns—the types of breaking water surface waves are discussed in more detail below. Certain other effects in fluid dynamics have also been termed "breaking waves," partly by analogy with water surface waves. In meteorology, atmospheric gravity waves are said to break when the wave produces regions where the potential temperature decreases with height, leading to energy dissipation through convective instability; likewise, Rossby waves are said to break wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drag (physics)
In fluid dynamics, drag (sometimes called air resistance, a type of friction, or fluid resistance, another type of friction or fluid friction) is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers (or surfaces) or between a fluid and a solid surface. Unlike other resistive forces, such as dry friction, which are nearly independent of velocity, the drag force depends on velocity. Drag force is proportional to the velocity for low-speed flow and the squared velocity for high speed flow, where the distinction between low and high speed is measured by the Reynolds number. Even though the ultimate cause of drag is viscous friction, turbulent drag is independent of viscosity. Drag forces always tend to decrease fluid velocity relative to the solid object in the fluid's path. Examples Examples of drag include the component of the net aerodynamic or hydrodynamic force acting opposite to the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinearity
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave–current Interaction
In fluid dynamics, wave–current interaction is the interaction between surface gravity waves and a mean flow. The interaction implies an exchange of energy, so after the start of the interaction both the waves and the mean flow are affected. For depth- integrated and phase-averaged flows, the quantity of primary importance for the dynamics of the interaction is the wave radiation stress tensor. Wave–current interaction is also one of the possible mechanisms for the occurrence of rogue waves, such as in the Agulhas Current. When a wave group encounters an opposing current, the waves in the group may pile up on top of each other which will propagate into a rogue wave. Classification identifies five major sub-classes within wave–current interaction: * interaction of waves with a large-scale current field, with slow – as compared to the wavelength – two-dimensional horizontal variations of the current fields; * interaction of waves with small-scale current changes (in co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Eckart
Carl Henry Eckart (May 4, 1902 – October 23, 1973) was an American physicist, physical oceanographer, geophysicist, and administrator. He co-developed the Wigner–Eckart theorem and is also known for the Eckart conditions in quantum mechanics, and the Eckart–Young theorem in linear algebra. Early life Eckart was born in St. Louis, Missouri. He began college in 1919 at Washington University in St. Louis where he received his B.S. and M.S. degrees with a major in engineering. However, due to Arthur Holly Compton, a physics faculty member and later Chancellor, Eckart was influenced to continue his education in physics at Princeton, where he went in 1923 on an Edison Lamp Works Research Fellowship. Eckart was awarded his Ph.D. in 1925.Eckart Biography – The National Academies Press [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |