|
Middle Term
In logic, a middle term is a term that appears (as a subject or predicate of a categorical proposition) in both premises but not in the conclusion of a categorical syllogism. Example: :Major premise: All men are mortal. :Minor premise A syllogism ( grc-gre, συλλογισμός, ''syllogismos'', 'conclusion, inference') is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true ...: Socrates is a man. :Conclusion: Socrates is mortal. The middle term is bolded above. References {{logic-stub Term logic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usually un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term (logic)
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact. A first-order term is recursively constructed from constant symbols, variables and function symbols. An expression formed by applying a predicate symbol to an appropriate number of terms is called an atomic formula, which evaluates to true or false in bivalent logics, given an interpretation. For example, is a term built from the constant 1, the variable , and the binary function symbols and ; it is part of the atomic formula which evaluates to true for each real-numbered value of . Besides in logic, terms play important roles in universal algebra, and rewriting systems. Formal definition Given a set ''V'' of variable symbols, a set ''C'' of constant symbols and sets ''F''''n'' of ''n''-ary fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
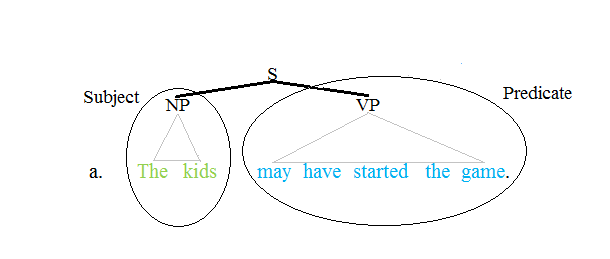
Subject (grammar)
The subject in a simple English sentence such as ''John runs'', ''John is a teacher'', or ''John drives a car'', is the person or thing about whom the statement is made, in this case ''John''. Traditionally the subject is the word or phrase which controls the verb in the clause, that is to say with which the verb agrees (''John is'' but ''John and Mary are''). If there is no verb, as in ''John what an idiot!'', or if the verb has a different subject, as in ''John I can't stand him!'', then 'John' is not considered to be the grammatical subject, but can be described as the ''topic'' of the sentence. While these definitions apply to simple English sentences, defining the subject is more difficult in more complex sentences and in languages other than English. For example, in the sentence ''It is difficult to learn French'', the subject seems to be the word ''it'', and yet arguably the real subject (the thing that is difficult) is ''to learn French''. A sentence such as ''It was J ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate (grammar)
The term predicate is used in one of two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject, and the other views it as just the main content verb or associated predicative expression of a clause. Thus, by the first definition the predicate of the sentence ''Frank likes cake'' is ''likes cake''. By the second definition, the predicate of the same sentence is just the content verb ''likes'', whereby ''Frank'' and ''cake'' are the arguments of this predicate. Differences between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of predicates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Proposition
In logic, a categorical proposition, or categorical statement, is a proposition that asserts or denies that all or some of the members of one category (the ''subject term'') are included in another (the ''predicate term''). The study of arguments using categorical statements (i.e., syllogisms) forms an important branch of deductive reasoning that began with the Ancient Greeks. The Ancient Greeks such as Aristotle identified four primary distinct types of categorical proposition and gave them standard forms (now often called ''A'', ''E'', ''I'', and ''O''). If, abstractly, the subject category is named ''S'' and the predicate category is named ''P'', the four standard forms are: *All ''S'' are ''P''. (''A'' form, \forall _\rightarrow P_xequiv \forall neg S_\lor P_x/math>) *No ''S'' are ''P''. (''E'' form, \forall _\rightarrow \neg P_xequiv \forall neg S_\lor \neg P_x/math>) *Some ''S'' are ''P''. (''I'' form, \exists _\land P_x/math>) *Some ''S'' are not ''P''. (''O'' form, \ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Premise
A premise or premiss is a true or false statement that helps form the body of an argument, which logically leads to a true or false conclusion. A premise makes a declarative statement about its subject matter which enables a reader to either agree or disagree with the premise in question, and in doing so understand the logical assumptions of the argument. If a premise is logically false, then the conclusion, which follows from all of the premises of the argument, must also be false—unless the conclusion is supported by a logically valid argument which the reader agrees with. Therefore, if the reader disagrees with any one of the argument's premises, they have a logical basis to reject the conclusion of the argument. Explanation In logic, an argument requires a set of at least two declarative sentences (or "propositions") known as the "premises" (or "premisses"), along with another declarative sentence (or "proposition"), known as the conclusion. This structure of two prem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Syllogism
A syllogism ( grc-gre, συλλογισμός, ''syllogismos'', 'conclusion, inference') is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true. In its earliest form (defined by Aristotle in his 350 BCE book ''Prior Analytics''), a syllogism arises when two true premises (propositions or statements) validly imply a conclusion, or the main point that the argument aims to get across. For example, knowing that all men are mortal (major premise) and that Socrates is a man (minor premise), we may validly conclude that Socrates is mortal. Syllogistic arguments are usually represented in a three-line form: All men are mortal. Socrates is a man. Therefore, Socrates is mortal.In antiquity, two rival syllogistic theories existed: Aristotelian syllogism and Stoic syllogism. From the Middle Ages onwards, ''categorical syllogism'' and ''syllogism'' were usually used interchangeably. This ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Premise
A syllogism ( grc-gre, συλλογισμός, ''syllogismos'', 'conclusion, inference') is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true. In its earliest form (defined by Aristotle in his 350 BCE book ''Prior Analytics''), a syllogism arises when two true premises (propositions or statements) validly imply a conclusion, or the main point that the argument aims to get across. For example, knowing that all men are mortal (major premise) and that Socrates is a man (minor premise), we may validly conclude that Socrates is mortal. Syllogistic arguments are usually represented in a three-line form: All men are mortal. Socrates is a man. Therefore, Socrates is mortal.In antiquity, two rival syllogistic theories existed: Aristotelian syllogism and Stoic syllogism. From the Middle Ages onwards, ''categorical syllogism'' and ''syllogism'' were usually used interchangeably. This ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
