|
Micromagnetics By Zureks
Micromagnetics is a field of physics dealing with the prediction of magnetic behaviors at sub-micrometer length scales. The length scales considered are large enough for the atomic structure of the material to be ignored (the continuum approximation), yet small enough to resolve magnetic structures such as domain walls or vortices. Micromagnetics can deal with static equilibria, by minimizing the magnetic energy, and with dynamic behavior, by solving the time-dependent dynamical equation. History Micromagnetics as a field (''i.e.'', that deals specifically with the behaviour of ferromagnetic materials at sub-micrometer length scales) was introduced in 1963 when William Fuller Brown Jr. published a paper on antiparallel domain wall structures. Until comparatively recently computational micromagnetics has been prohibitively expensive in terms of computational power, but smaller problems are now solvable on a modern desktop PC. Static micromagnetics The purpose of static micro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady (not changing with time). It is the magnetic analogue of electrostatics, where the electric charge, charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast Magnetization reversal, magnetic switching events that occur on time scales of nanoseconds or less. Magnetostatics is even a good approximation when the currents are not static – as long as the currents do not alternating current, alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic storage devices as in computer memory. Applications Magnetostatics as a special case of Maxwell's equations Starting from Maxwell's equations and assuming that charges are either fixed or move as a steady current \mathbf, the equations separate into two equations for the electric field (see electrostatics) and two for the magnetic fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
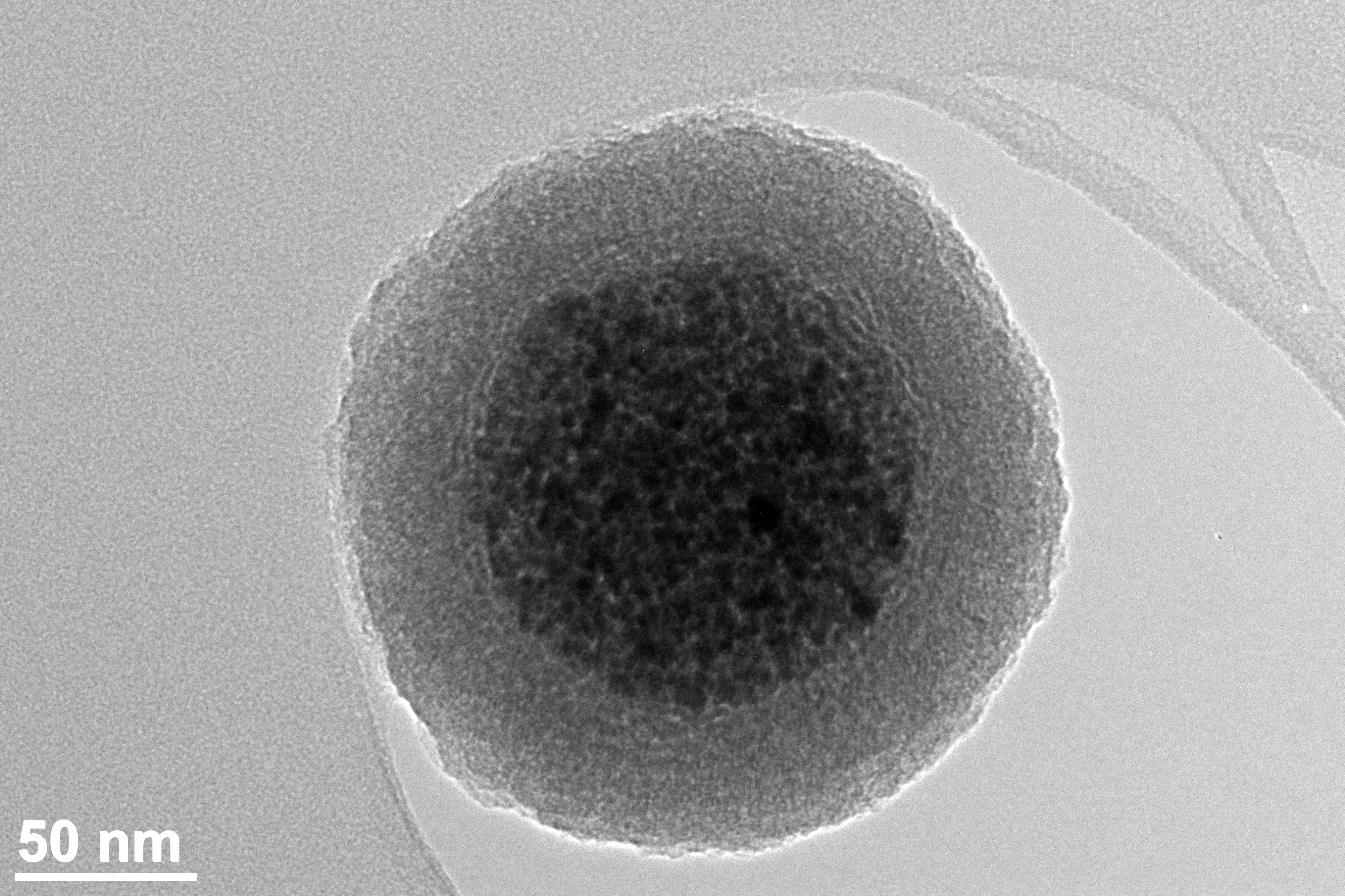
Magnetic Nanoparticles
Magnetic nanoparticles are a class of nanoparticle that can be manipulated using magnetic fields. Such particles commonly consist of two components, a magnetic material, often iron, nickel and cobalt, and a chemical component that has functionality. While nanoparticles are smaller than 1 micrometer in diameter (typically 1–100 nanometers), the larger microbeads are 0.5–500 micrometer in diameter. Magnetic nanoparticle clusters that are composed of a number of individual magnetic nanoparticles are known as magnetic nanobeads with a diameter of 50–200 nanometers. Magnetic nanoparticle clusters are a basis for their further magnetic assembly into magnetic nanochains. The magnetic nanoparticles have been the focus of much research recently because they possess attractive properties which could see potential use in catalysis including nanomaterial-based catalysts, biomedicine and tissue specific targeting, antimicrobial agents, magnetically tunable colloidal photonic crystals, mic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetism
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particles give rise to a magnetic field, which acts on other currents and magnetic moments. Magnetism is one aspect of the combined phenomena of electromagnetism. The most familiar effects occur in ferromagnetic materials, which are strongly attracted by magnetic fields and can be magnetized to become permanent magnets, producing magnetic fields themselves. Demagnetizing a magnet is also possible. Only a few substances are ferromagnetic; the most common ones are iron, cobalt, and nickel and their alloys. The rare-earth metals neodymium and samarium are less common examples. The prefix ' refers to iron because permanent magnetism was first observed in lodestone, a form of natural iron ore called magnetite, Fe3O4. All substances exhibit some type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Technology
Information technology (IT) is the use of computers to create, process, store, retrieve, and exchange all kinds of data . and information. IT forms part of information and communications technology (ICT). An information technology system (IT system) is generally an information system, a communications system, or, more specifically speaking, a computer system — including all hardware, software, and peripheral equipment — operated by a limited group of IT users. Although humans have been storing, retrieving, manipulating, and communicating information since the earliest writing systems were developed, the term ''information technology'' in its modern sense first appeared in a 1958 article published in the ''Harvard Business Review''; authors Harold J. Leavitt and Thomas L. Whisler commented that "the new technology does not yet have a single established name. We shall call it information technology (IT)." Their definition consists of three categories: techniques for pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vortex
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil. Vortices are a major component of turbulent flow. The distribution of velocity, vorticity (the curl of the flow velocity), as well as the concept of circulation are used to characterise vortices. In most vortices, the fluid flow velocity is greatest next to its axis and decreases in inverse proportion to the distance from the axis. In the absence of external forces, viscous friction within the fluid tends to organise the flow into a collection of irrotational vortices, possibly superimposed to larger-scale flows, including larger-scale vortices. Once formed, vortices can move, stretch, twist, and interact in complex ways. A moving vortex carries s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damping Ratio
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Larmor Precession
In physics, Larmor precession (named after Joseph Larmor) is the precession of the magnetic moment of an object about an external magnetic field. The phenomenon is conceptually similar to the precession of a tilted classical gyroscope in an external torque-exerting gravitational field. Objects with a magnetic moment also have angular momentum and effective internal electric current proportional to their angular momentum; these include electrons, protons, other fermions, many atomic and nuclear physics, nuclear systems, as well as classical macroscopic systems. The external magnetic field exerts a torque on the magnetic moment, :\vec = \vec\times\vec = \gamma\vec\times\vec, where \vec is the torque, \vec is the magnetic dipole moment, \vec is the angular momentum vector, \vec is the external magnetic field, \times symbolizes the cross product, and \gamma is the gyromagnetic ratio which gives the proportionality constant between the magnetic moment and the angular momentum. The an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damped Magnetization Precession
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |