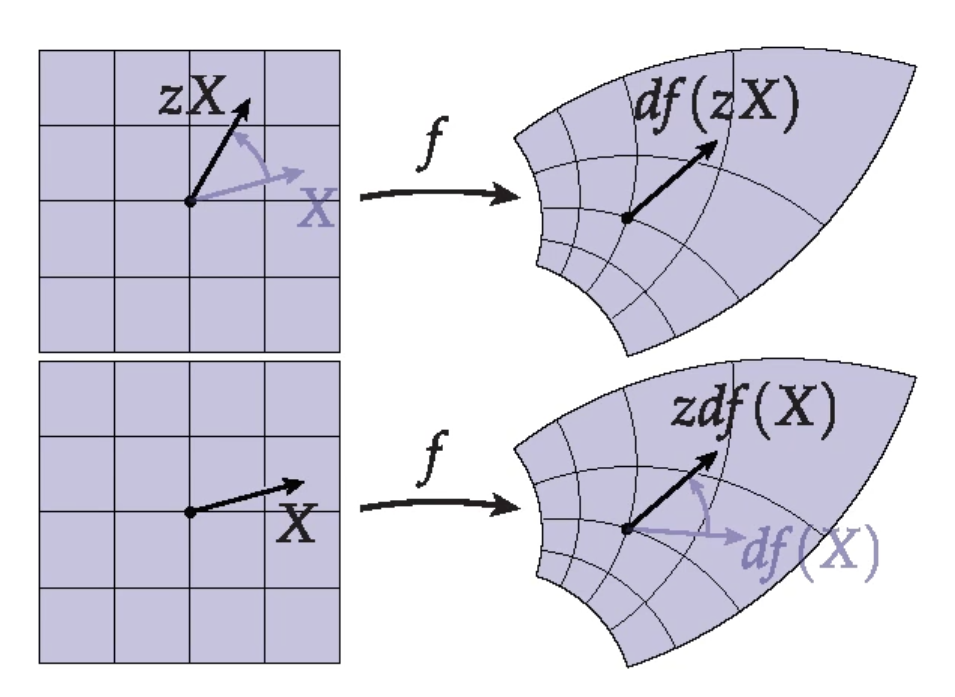
|
Maximum-modulus Theorem
In mathematics, the maximum modulus principle in complex analysis states that if ''f'' is a holomorphic function, then the modulus , ''f'' , cannot exhibit a strict local maximum that is properly within the domain of ''f''. In other words, either ''f'' is locally a constant function, or, for any point ''z''0 inside the domain of ''f'' there exist other points arbitrarily close to ''z''0 at which , ''f'' , takes larger values. Formal statement Let ''f'' be a holomorphic function on some connected open subset ''D'' of the complex plane ℂ and taking complex values. If ''z''0 is a point in ''D'' such that :, f(z_0), \ge , f(z), for all ''z'' in some neighborhood of ''z''0, then ''f'' is constant on ''D''. This statement can be viewed as a special case of the open mapping theorem, which states that a nonconstant holomorphic function maps open sets to open sets: If , ''f'', attains a local maximum at ''z'', then the image of a sufficiently small open neighborhood of ''z'' ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Modulus Principle
In mathematics, the maximum modulus principle in complex analysis states that if ''f'' is a holomorphic function, then the modulus , ''f'' , cannot exhibit a strict local maximum that is properly within the domain of ''f''. In other words, either ''f'' is locally a constant function, or, for any point ''z''0 inside the domain of ''f'' there exist other points arbitrarily close to ''z''0 at which , ''f'' , takes larger values. Formal statement Let ''f'' be a holomorphic function on some connected open subset ''D'' of the complex plane ℂ and taking complex values. If ''z''0 is a point in ''D'' such that :, f(z_0), \ge , f(z), for all ''z'' in some neighborhood of ''z''0, then ''f'' is constant on ''D''. This statement can be viewed as a special case of the open mapping theorem, which states that a nonconstant holomorphic function maps open sets to open sets: If , ''f'', attains a local maximum at ''z'', then the image of a sufficiently small open neighborhood of ''z'' ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadamard Three-lines Theorem
In complex analysis, a branch of mathematics, the Hadamard three-lines theorem is a result about the behaviour of holomorphic functions defined in regions bounded by parallel lines in the complex plane. The theorem is named after the French mathematician Jacques Hadamard. Statement Define F(z) by : F(z)=f(z) M(a)^M(b)^ where , F(z), \leq 1 on the edges of the strip. The result follows once it is shown that the inequality also holds in the interior of the strip. After an affine transformation in the coordinate z, it can be assumed that a = 0 and b = 1. The function : F_n(z) = F(z) e^e^ tends to 0 as , z, tends to infinity and satisfies , F_n, \leq 1 on the boundary of the strip. The maximum modulus principle can therefore be applied to F_n in the strip. So , F_n(z), \leq 1. Because F_n(z) tends to F(z) as n tends to infinity, it follows that , F(z), \leq 1. ∎ Applications The three-line theorem can be used to prove the Hadamard three-circle theorem for a boun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borel–Carathéodory Theorem
In mathematics, the Borel–Carathéodory theorem in complex analysis shows that an analytic function may be bounded by its real part. It is an application of the maximum modulus principle. It is named for Émile Borel and Constantin Carathéodory. Statement of the theorem Let a function f be analytic on a closed disc of radius ''R'' centered at the origin Origin(s) or The Origin may refer to: Arts, entertainment, and media Comics and manga * Origin (comics), ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002 * The Origin (Buffy comic), ''The Origin'' (Bu .... Suppose that ''r'' 1, so we may assume ''f'' is nonconstant. First let ''f''(0) = 0. Since Re ''f'' is harmonic, Re ''f''(0) is equal to the average of its values around any circle centered at 0. That is, : \operatorname f(0) = \frac \int_ \operatorname f(z) dz. Since ''f'' is regular and nonconstant, we have that Re ''f'' is also nonconstant. Since Re ''f''(0) = 0, we must ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phragmén–Lindelöf Principle
In complex analysis, the Phragmén–Lindelöf principle (or method), first formulated by Lars Edvard Phragmén (1863–1937) and Ernst Leonard Lindelöf (1870–1946) in 1908, is a technique which employs an auxiliary, parameterized function to prove the boundedness of a holomorphic function f (i.e, , f(z), Background In the theory of complex functions, it is known that the modulus (absolute value) of a |
Schwarz's Lemma
In mathematics, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis about holomorphic functions from the open unit disk to itself. The lemma is less celebrated than deeper theorems, such as the Riemann mapping theorem, which it helps to prove. It is, however, one of the simplest results capturing the rigidity of holomorphic functions. Statement Let \mathbf = \ be the open unit disk in the complex plane \mathbb centered at the origin, and let f : \mathbf\rightarrow \mathbb be a holomorphic map such that f(0) = 0 and , f(z), \leq 1 on \mathbf. Then , f(z), \leq , z, for all z \in \mathbf, and , f'(0), \leq 1. Moreover, if , f(z), = , z, for some non-zero z or , f'(0), = 1, then f(z) = az for some a \in \mathbb with , a, = 1.Theorem 5.34 in Proof The proof is a straightforward application of the maximum modulus principle on the function :g(z) = \begin \frac\, & \mbox z \neq 0 \\ f'(0) & \mbox z = 0, \end which is holomorphic on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Algebra
The fundamental theorem of algebra, also known as d'Alembert's theorem, or the d'Alembert–Gauss theorem, states that every non- constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero. Equivalently (by definition), the theorem states that the field of complex numbers is algebraically closed. The theorem is also stated as follows: every non-zero, single-variable, degree ''n'' polynomial with complex coefficients has, counted with multiplicity, exactly ''n'' complex roots. The equivalence of the two statements can be proven through the use of successive polynomial division. Despite its name, there is no purely algebraic proof of the theorem, since any proof must use some form of the analytic completeness of the real numbers, which is not an algebraic concept. Additionally, it is not fundamental for modern algebra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy's Integral Formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentiation, like integration, behaves well under uniform limits – a result that does not hold in real analysis. Theorem Let be an open subset of the complex plane , and suppose the closed disk defined as :D = \bigl\ is completely contained in . Let be a holomorphic function, and let be the circle, oriented counterclockwise, forming the boundary of . Then for every in the interior of , :f(a) = \frac \oint_\gamma \frac\,dz.\, The proof of this statement uses the Cauchy integral theorem and like that theorem, it only requires t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Riemann Equations
In the field of complex analysis in mathematics, the Cauchy–Riemann equations, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which, together with certain continuity and differentiability criteria, form a necessary and sufficient condition for a complex function to be holomorphic (complex differentiable). This system of equations first appeared in the work of Jean le Rond d'Alembert. Later, Leonhard Euler connected this system to the analytic functions. Cauchy then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851. The Cauchy–Riemann equations on a pair of real-valued functions of two real variables and are the two equations: Typically ''u'' and ''v'' are taken to be the real and imaginary parts respectively of a complex-valued function of a single complex variable , . Suppose that and are real-differentiable at a point in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Principle
In the mathematical fields of partial differential equations and geometric analysis, the maximum principle is any of a collection of results and techniques of fundamental importance in the study of elliptic and parabolic differential equations. In the simplest case, consider a function of two variables such that :\frac+\frac=0. The weak maximum principle, in this setting, says that for any open precompact subset of the domain of , the maximum of on the closure of is achieved on the boundary of . The strong maximum principle says that, unless is a constant function, the maximum cannot also be achieved anywhere on itself. Such statements give a striking qualitative picture of solutions of the given differential equation. Such a qualitative picture can be extended to many kinds of differential equations. In many situations, one can also use such maximum principles to draw precise quantitative conclusions about solutions of differential equations, such as control over the size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f: U \to \mathbb R, where is an open subset of that satisfies Laplace's equation, that is, : \frac + \frac + \cdots + \frac = 0 everywhere on . This is usually written as : \nabla^2 f = 0 or :\Delta f = 0 Etymology of the term "harmonic" The descriptor "harmonic" in the name harmonic function originates from a point on a taut string which is undergoing harmonic motion. The solution to the differential equation for this type of motion can be written in terms of sines and cosines, functions which are thus referred to as ''harmonics''. Fourier analysis involves expanding functions on the unit circle in terms of a series of these harmonics. Considering higher dimensional analogues of the harmonics on the unit ''n''-sphere, one arrives at the spherical harmonics. These functions satisfy Laplace's equation and over time "harmonic" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
