|
Maxcut
For a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets and , such that the number of edges between and is as large as possible. Finding such a cut is known as the max-cut problem. The problem can be stated simply as follows. One wants a subset of the vertex set such that the number of edges between and the complementary subset is as large as possible. Equivalently, one wants a bipartite subgraph of the graph with as many edges as possible. There is a more general version of the problem called weighted max-cut, where each edge is associated with a real number, its weight, and the objective is to maximize the total weight of the edges between and its complement rather than the number of the edges. The weighted max-cut problem allowing both positive and negative weights can be trivially transformed into a weighted minimum cut problem by flipping the sign in all wei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
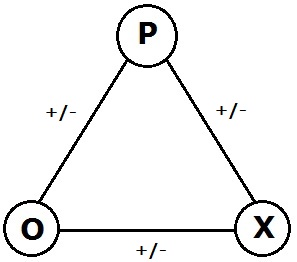
Signed Graphs
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are a n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karp's 21 NP-complete Problems
In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete. In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the boolean satisfiability problem is NP-complete (also called the Cook-Levin theorem) to show that there is a polynomial time many-one reduction from the boolean satisfiability problem to each of 21 combinatorial and graph theoretical computational problems, thereby showing that they are all NP-complete. This was one of the first demonstrations that many natural computational problems occurring throughout computer science are computationally intractable, and it drove interest in the study of NP-completeness and the P versus NP problem. The problems Karp's 21 problems are shown below, many with their original names. The nesting indicates the direction of the reductions used. For example, Knapsack was shown to be NP-complete by reducing Exact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Randomized Algorithm
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output (or both) are random variables. One has to distinguish between algorithms that use the random input so that they always terminate with the correct answer, but where the expected running time is finite (Las Vegas algorithms, for example Quicksort), and algorithms which have a chance of producing an incorrect result (Monte Carlo algorithms, for example the Monte Carlo algorithm for the MFAS problem) or fail to produce a result either by signaling a failure or failing to terminate. In some cases, probabilistic algorithms are the only practical means of solving a problem. In common practice, randomized algor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Ratio
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxSNP
In computational complexity theory, SNP (from Strict NP) is a complexity class containing a limited subset of NP based on its logical characterization in terms of graph-theoretical properties. It forms the basis for the definition of the class MaxSNP of optimization problems. It is defined as the class of problems that are properties of relational structures (such as graphs) expressible by a second-order logic formula of the following form: : \exists S_1 \dots \exists S_\ell \, \forall v_1 \dots \forall v_m \,\phi(R_1,\dots,R_k,S_1,\dots,S_\ell,v_1,\dots,v_m), where R_1,\dots,R_k are relations of the structure (such as the adjacency relation, for a graph), S_1,\dots,S_\ell are unknown relations (sets of tuples of vertices), and \phi is a quantifier-free formula: any boolean combination of the relations. That is, only existential second-order quantification (over relations) is allowed and only universal first-order quantification (over vertices) is allowed. If existential quantific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant-factor Approximation Algorithm
In computational complexity theory, the class APX (an abbreviation of "approximable") is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant (or constant-factor approximation algorithms for short). In simple terms, problems in this class have efficient algorithms that can find an answer within some fixed multiplicative factor of the optimal answer. An approximation algorithm is called an f(n)-approximation algorithm for input size n if it can be proven that the solution that the algorithm finds is at most a multiplicative factor of f(n) times worse than the optimal solution. Here, f(n) is called the ''approximation ratio''. Problems in APX are those with algorithms for which the approximation ratio f(n) is a constant c. The approximation ratio is conventionally stated greater than 1. In the case of minimization problems, f(n) is the found solution's score divided by the optimum solution's score, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winding Number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise. Winding numbers are fundamental objects of study in algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in string theory). Intuitive description Suppose we are given a closed, oriented curve in the ''xy'' plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin. When counting the total nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Graph
In the mathematical discipline of graph theory, the dual graph of a plane graph is a graph that has a vertex for each face of . The dual graph has an edge for each pair of faces in that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge of has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of . The definition of the dual depends on the choice of embedding of the graph , so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known). For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph. Historically, the first form of graph duality to be recognized was the association of the Platonic solids into pairs of dual polyhedra. Graph duality is a topological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Route Inspection Problem
In graph theory, a branch of mathematics and computer science, Guan's route problem, the Chinese postman problem, postman tour or route inspection problem is to find a shortest closed path or circuit that visits every edge of an (connected) undirected graph. When the graph has an Eulerian circuit (a closed walk that covers every edge once), that circuit is an optimal solution. Otherwise, the optimization problem is to find the smallest number of graph edges to duplicate (or the subset of edges with the minimum possible total weight) so that the resulting multigraph does have an Eulerian circuit. It can be solved in polynomial time. The problem was originally studied by the Chinese mathematician Kwan Mei-Ko in 1960, whose Chinese paper was translated into English in 1962. The original name "Chinese postman problem" was coined in his honor; different sources credit the coinage either to Alan J. Goldman or Jack Edmonds, both of whom were at the U.S. National Bureau of Standards at t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planar Graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points. Every graph that can be drawn on a plane can be drawn on the sphere as well, and vice versa, by means of stereographic projection. Plane graphs can be encoded by combinatorial maps or rotation systems. An equivalence class of topologically equivalent drawings on the sphere, usually with additional assumptions such as the absence of isthmuses, is called a pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
