|
Mathematical Visualization
Mathematical phenomena can be understood and explored via visualization. Classically this consisted of two-dimensional drawings or building three-dimensional models (particularly plaster models in the 19th and early 20th century), while today it most frequently consists of using computers to make static two or three dimensional drawings, animations, or interactive programs. Writing programs to visualize mathematics is an aspect of computational geometry. Applications Mathematical visualization is used throughout mathematics, particularly in the fields of geometry and analysis. Notable examples include plane curves, space curves, polyhedra, ordinary differential equations, partial differential equations (particularly numerical solutions, as in fluid dynamics or minimal surfaces such as soap films), conformal maps, fractals, and chaos. Geometry Geometry can be defined as the study of shapes their size, angles, dimensions and proportions Linear algebra Complex analysis I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandel Zoom 00 Mandelbrot Set
Mandel is a surname (and occasional given name) that occurs in multiple cultures and languages. It is a Dutch, German and Jewish surname, meaning "almond", from the Middle High German and Middle Dutch ''mandel''.''Dictionary of American Family Names''"Mandel Family History" Oxford University Press, 2013. Retrieved on 18 January 2016. Mandel can be a locational surname, from places called Mandel, such as Mandel, Germany. Mandel may also be a Dutch surname, from the Middle Dutch ''mandele'', meaning a number of sheaves of harvested wheat. Notable people * Alon Mandel (born 1988), Israeli swimmer * Babaloo Mandel (born 1949), American screenwriter *David Mandel (born 1970), American television producer and writer * Edgar Mandel (born 1928), German actor * Eli Mandel (1922–1992), Canadian writer *Emily St. John Mandel (born 1979), Canadian novelist * Emmanuil Mandel (1925–2018), Russian poet * Ernest Mandel (1923–1995), Belgian politician, professor and writer * Frank Mande ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to roundin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cellular Automata
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of '' states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that determines the new state of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stephen Wolfram
Stephen Wolfram (; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer science, mathematics, and theoretical physics. In 2012, he was named a fellow of the American Mathematical Society. He is currently an adjunct professor at the University of Illinois Department of Computer Science. As a businessman, he is the founder and CEO of the software company Wolfram Research where he works as chief designer of Mathematica and the Wolfram Alpha answer engine. Early life Family Stephen Wolfram was born in London in 1959 to Hugo and Sybil Wolfram, both German Jewish refugees to the United Kingdom. His maternal grandmother was British psychoanalyst Kate Friedlander. Wolfram's father, Hugo Wolfram, was a textile manufacturer and served as managing director of the Lurex Company—makers of the fabric Lurex. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Network Analysis Visualization
Social organisms, including human(s), live collectively in interacting populations. This interaction is considered social whether they are aware of it or not, and whether the exchange is voluntary or not. Etymology The word "social" derives from the Latin word ''socii'' ("allies"). It is particularly derived from the Italian ''Socii'' states, historical allies of the Roman Republic (although they rebelled against Rome in the Social War of 91–87 BC). Social theorists In the view of Karl MarxMorrison, Ken. ''Marx, Durkheim, Weber. Formations of modern social thought'', human beings are intrinsically, necessarily and by definition social beings who, beyond being "gregarious creatures", cannot survive and meet their needs other than through social co-operation and association. Their social characteristics are therefore to a large extent an objectively given fact, stamped on them from birth and affirmed by socialization processes; and, according to Marx, in producing and reproducin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Table
In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3 (in topology, a circle is not bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Costa's Minimal Surface
In mathematics, Costa's minimal surface, is an embedded minimal surface discovered in 1982 by the Brazilian mathematician Celso José da Costa. It is also a surface of finite topology, which means that it can be formed by puncturing a compact surface. Topologically, it is a thrice-punctured torus. Until its discovery, the plane, helicoid and the catenoid were believed to be the only embedded minimal surfaces that could be formed by puncturing a compact surface. The Costa surface evolves from a torus, which is deformed until the planar end becomes catenoidal. Defining these surfaces on rectangular tori of arbitrary dimensions yields the Costa surface. Its discovery triggered research and discovery into several new surfaces and open conjectures In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorenz Attractor Yb
Lorenz is an originally German name derived from the Roman surname Laurentius, which means "from Laurentum". Given name People with the given name Lorenz include: * Prince Lorenz of Belgium (born 1955), member of the Belgian royal family by his marriage with Princess Astrid of Belgium * Lorenz Böhler (1885–1973), Austrian trauma surgeon * Lorenz Hart (1895–1943), American lyricist, half of the famed Broadway songwriting team Rodgers and Hart * Lorenz Lange (1690–1752), Russian official in Siberia * Lorenz Oken (1779–1851), German naturalist * Lorenz of Werle (1338/40–1393/94), Lord of Werle-Güstrow Surname People with the name surname Lorenz include: * Adolf Lorenz (1854–1946), Austrian surgeon * Alfred Lorenz (1868–1939), Austrian-German musical analyst * Angela Lorenz (born 1965), American artist * Barbara Lorenz, make-up artist * Carl Lorenz (1913–1993), German cyclist * Christian Lorenz (born 1966), German musician * Edward Norton Lorenz (1917–200 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
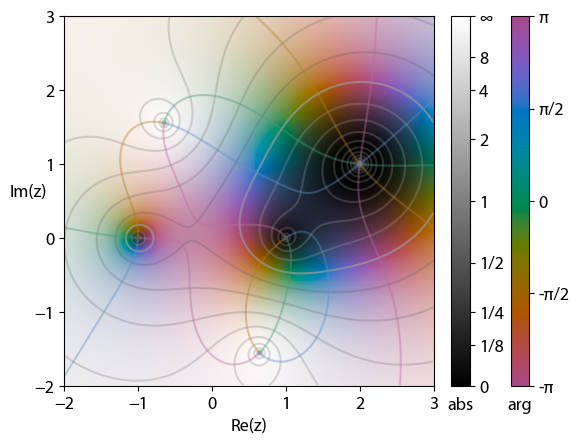
Domain Coloring
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the complex plane. By assigning points on the complex plane to different colors and brightness, domain coloring allows for a function from the complex plane to itself — whose graph would normally require four space dimensions — to be easily represented and understood. This provides insight to the fluidity of complex functions and shows natural geometric extensions of real functions. Motivation A graph of a real function can be drawn in two dimensions because there are two represented variables, x and y. However, complex numbers are represented by two variables and therefore two dimensions; this means that representing a complex function (more precisely, a complex-valued function of one complex variable f: \mathbb \to \mathbb) requires the visualization of four dimensions. One way to achieve that is with a Riemann surface, but anot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear engineering, nuclear, aerospace engineering, aerospace, mechanical engineering, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is Analyticity of holomorphic functions, analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
