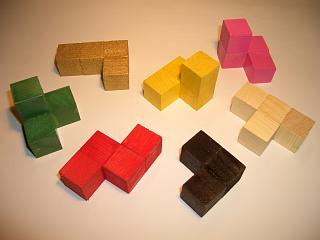|
Mathematical Games (column)
Over a period of 24 years (January 1957 – December 1980), Martin Gardner wrote 288 consecutive monthly "Mathematical Games" columns for ''Scientific American'' magazine. During the next years, until June 1986, Gardner wrote 9 more columns, bringing his total to 297. During this period other authors wrote most of the columns. In 1981, Gardner's column alternated with a new column by Douglas Hofstadter called "Metamagical_Themas#List_of_Hofstadter's_%22Metamagical_Themas%22_columns, Metamagical Themas" (an anagram of "Mathematical Games"). The table below lists Gardner's columns. Twelve of Gardner's columns provided the cover art for that month's magazine, indicated by "[cover]" in the table with a hyperlink to the cover. Other articles by Gardner Gardner wrote 5 other articles for ''Scientific American''. His flexagon article in December 1956 was in all but name the first article in the series of ''Mathematical Games'' columns and led directly to the series which began the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing magic, scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton.Martin (2010) He was a leading authority on Lewis Carroll; '' The Annotated Alice'', which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies.Martin Gardner obituary (2010) He had a lifelong interest in magic and illusion and in 1999, ''MAGIC'' magazine named him as one of the "10 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chirality (mathematics)
In geometry, a figure is chiral (and said to have chirality) if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by Rotation (mathematics), rotations and Translation (geometry), translations alone. An object that is not chiral is said to be ''achiral''. A chiral object and its mirror image are said to be enantiomorphs. The word ''chirality'' is derived from the Greek (cheir), the hand, the most familiar chiral object; the word ''enantiomorph'' stems from the Greek (enantios) 'opposite' + (morphe) 'form'. Examples Some chiral three-dimensional objects, such as the helix, can be assigned a right or left handedness, according to the right-hand rule. Many other familiar objects exhibit the same chiral symmetry of the human body, such as gloves and shoes. Right shoes differ from left shoes only by being mirror images of each other. In contrast thin gloves may not be considered chiral if you can wear them wiktionary:inside ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origami
) is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word ' to refer to designs which use cuts. In the detailed Japanese classification, origami is divided into stylized ceremonial origami (儀礼折り紙, ''girei origami'') and recreational origami (遊戯折り紙, ''yūgi origami''), and only recreational origami is generally recognized as origami. In Japan, ceremonial origami is generally called "origata" ( :ja:折形) to distinguish it from recreational origami. The term "origata" is one of the old terms for origami. The small number of basic origami folds can be combined in a variety of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eleusis (card Game)
''Eleusis'' is a shedding-type card game where one player chooses a secret rule to determine which cards can be played on top of others, and the other players attempt to determine the rule using inductive logic. The game was invented by Robert Abbott in 1956, and was first published by Martin Gardner in his Mathematical Games column in ''Scientific American'' magazine in June 1959. A revised version appeared in Gardner's July 1977 column. Eleusis is sometimes considered an analogy to the problems of scientific method. It can be compared with the card game Mao, which also has secret rules that can be learned inductively. The games of Penultima and commercially produced Zendo also feature players attempting to discover inductively a secret rule or rules thought of by a "Master" or "spectators" who declare plays legal or illegal on the basis of the rules. Rules The game is played by creating a row of cards in sequence. At the start of the game the dealer (known as "God") i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logic
Mathematical logic is the study of Logic#Formal logic, formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory (also known as computability theory). Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics. Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and Mathematical analysis, analysis. In the early 20th century it was shaped by David Hilbert's Hilbert's program, program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maze
A maze is a path or collection of paths, typically from an entrance to a goal. The word is used to refer both to branching tour puzzles through which the solver must find a route, and to simpler non-branching ("unicursal") patterns that lead unambiguously through a convoluted layout to a goal. The term "labyrinth" is generally synonymous with "maze", but can also connote specifically a unicursal pattern. The pathways and walls in a maze are typically fixed, but puzzles in which the walls and paths can change during the game are also categorised as mazes or tour puzzles. Construction Mazes have been built with a variety of materials. Some are relatively permanent, like Hedge maze, hedges, Turf maze, turf, walls, rooms, tiles, and paving stones or bricks. Others are deliberately transitory, like Corn maze, corn stalks, Straw maze, straw bales, books, snow, or in fields of crops such as cereal, corn or maize. Maize mazes can be very large; they are usually kept only for one g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solids
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the '' Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squaring The Square
Squaring the square is the problem of tessellation, tiling an integral square using only other integral squares. (An integral square is a square (geometry), square whose sides have integer length.) The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares. Perfect squared squares A "perfect" squared square is a square such that each of the smaller squares has a different size. Perfect squared squares were studied by R. Leonard Brooks, R. L. Brooks, Cedric Smith (statistician), C. A. B. Smith, Arthur Harold Stone, A. H. Stone and W. T. Tutte (wr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Torsion (mechanics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a Set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of List of continuity-related mathematical topics, continuity. Euclidean spaces, and, more generally, metric spaces are examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and Homotopy, homotopies. A property that is invariant under such deformations is a to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soma Cube
The Soma cube is a mechanical puzzle#Assembly, solid dissection puzzle invented by Danish polymath Piet Hein (scientist), Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Seven different Polycube, pieces made out of unit cubes must be assembled into a 3×3×3 cube. The pieces can also be used to make a variety of other Three-dimensional space, 3D shapes. The pieces of the Soma cube consist of all possible combinations of at most four unit cubes, joined at their faces, such that at least one inside corner is formed. There are no combinations of one or two cubes that satisfy this condition, but one combination of three cubes and six combinations of four cubes that do. Thus, 3 + (6 × 4) is 27, which is exactly the number of cells in a 3×3×3 cube. Of these seven combinations, two are mirror images of each other (see Chirality (mathematics), Chirality). The Soma cube was popularized by Martin Gardner in the September 1958 Mathematical Games ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brain-teasers
A brain teaser is a form of puzzle that requires thought to solve. It often requires thinking in unconventional ways with given constraints in mind; sometimes it also involves lateral thinking. Logic puzzles and riddles are specific types of brain teasers. One of the earliest known brain teaser enthusiasts was the Greek mathematician Archimedes. He devised mathematical problems for his contemporaries to solve. Example :Q: ''If three hens lay three eggs in three days, how many eggs does a (statistical) hen lay in one day?'' :A1: ''One third.'' (Note: 3 hens = 3 eggs / 3 days → 3 hens = (3 / 3) (eggs / days) → 1 hen = (1 / 3) (egg / days)) :A2: ''Zero or one'' (it's hard to lay a third of an egg). One can argue about the answers of many brain teasers; in the given example with hens, one might claim that all the eggs in the question were laid in the first day, so the answer would be three. :Q: ''Mary's father has five daughters: 1. Nana, 2. Nene, 3. Nini, 4. Nono. What is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book '' Disquisitiones Arithmeticae'', published in 1801. A familiar example of modular arithmetic is the hour hand on a 12-hour clock. If the hour hand points to 7 now, then 8 hours later it will point to 3. Ordinary addition would result in , but 15 reads as 3 on the clock face. This is because the hour hand makes one rotation every 12 hours and the hour number starts over when the hour hand passes 12. We say that 15 is ''congruent'' to 3 modulo 12, written 15 ≡ 3 (mod 12), so that 7 + 8 ≡ 3 (mod 12). Similarly, if one starts at 12 and waits 8 hours, the hour hand will be at 8. If one instead waited twice as long, 16 hours, the hour hand would be on 4. This ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |