|
Markov Arrival Process
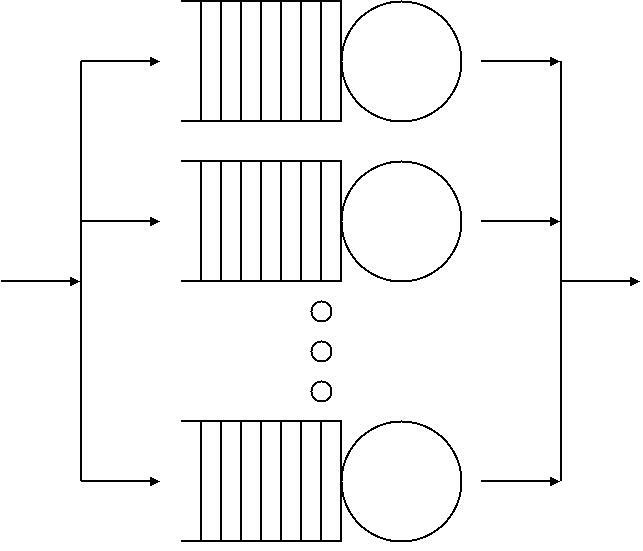
In queueing theory, a discipline within the mathematical theory of probability, a Markovian arrival process (MAP or MArP) is a mathematical model for the time between job arrivals to a system. The simplest such process is a Poisson process where the time between each arrival is exponentially distributed. The processes were first suggested by Neuts in 1979. Definition A Markov arrival process is defined by two matrices, ''D''0 and ''D''1 where elements of ''D''0 represent hidden transitions and elements of ''D''1 observable transitions. The block matrix ''Q'' below is a transition rate matrix for a continuous-time Markov chain. : Q=\left begin D_&D_&0&0&\dots\\ 0&D_&D_&0&\dots\\ 0&0&D_&D_&\dots\\ \vdots & \vdots & \ddots & \ddots & \ddots \end\right; . The simplest example is a Poisson process where ''D''0 = −''λ'' and ''D''1 = ''λ'' where there is only one possible transition, it is observable, and occurs at rate ''λ''. For ''Q'' to be a valid tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Theory
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang when he created models to describe the system of Copenhagen Telephone Exchange company, a Danish company. The ideas have since seen applications including telecommunication, traffic engineering, computing and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is ''Queueing Systems''. Single queueing nodes A queue, or queueing no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Process
In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy,G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of statistical planning and inference'', 50(3):311–326, 1996. biology,H. G. Othmer, S. R. Dunbar, and W. Alt. Models of dispersal in biological systems. ''Journal of mathematical biology'', 26(3):263–298, 1988. ecology,H. Thompson. Spatial point processes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Matrix
In mathematics, a block matrix or a partitioned matrix is a matrix that is '' interpreted'' as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned. This notion can be made more precise for an n by m matrix M by partitioning n into a collection \text, and then partitioning m into a collection \text. The original matrix is then considered as the "total" of these groups, in the sense that the (i, j) entry of the original matrix corresponds in a 1-to-1 way with some (s, t) offset entry of some (x,y), where x \in \text and y \in \text. Block matrix algebra arises in general from biproducts in categories of mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Rate Matrix
Transition or transitional may refer to: Mathematics, science, and technology Biology * Transition (genetics), a point mutation that changes a purine nucleotide to another purine (A ↔ G) or a pyrimidine nucleotide to another pyrimidine (C ↔ T) * Transitional fossil, any fossilized remains of a lifeform that exhibits the characteristics of two distinct taxonomic groups * A phase during childbirth contractions during which the cervix completes its dilation Gender and sex * Gender transitioning, the process of changing one's gender presentation to accord with one's internal sense of one's gender – the idea of what it means to be a man or woman * Sex reassignment therapy, the physical aspect of a gender transition Physics * Phase transition, a transformation of the state of matter; for example, the change between a solid and a liquid, between liquid and gas or between gas and plasma * Quantum phase transition, a phase transformation between different quantum phases * Quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous-time Markov Chain
A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state. An example of a CTMC with three states \ is as follows: the process makes a transition after the amount of time specified by the holding time—an exponential random variable E_i, where ''i'' is its current state. Each random variable is independent and such that E_0\sim \text(6), E_1\sim \text(12) and E_2\sim \text(18). When a transition is to be made, the process moves according to the jump chain, a discrete-time Markov chain with stochastic matrix: :\begin 0 & \frac & \frac \\ \frac & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase-type Distribution
A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the states of the Markov process represents one of the phases. It has a discrete-time equivalent the discrete phase-type distribution. The set of phase-type distributions is dense in the field of all positive-valued distributions, that is, it can be used to approximate any positive-valued distribution. Definition Consider a continuous-time Markov process with ''m'' + 1 states, where ''m'' ≥ 1, such that the states 1,...,''m'' are transient states and state 0 is an absorbing state. Further, let the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation–maximization Algorithm
In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the ''E'' step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step. History The EM algorithm was explained and given its name in a classic 1977 paper by Arthur Dempster, Nan Laird, and Donald Rubin. They pointed out that the method had been "proposed many times in special circumstances" by earlier authors. One of the earliest is the gene-counting method for estimating alle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. As of 2020, MATLAB has more than 4 million users worldwide. They come from various backgrounds of engineering, science, and economics. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was based on his 1960s PhD thesis. Moler became a math professor at the University of New Mexico an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Arrival Process
In queueing theory, a discipline within the mathematical theory of probability, a rational arrival process (RAP) is a mathematical model for the time between job arrivals to a system. It extends the concept of a Markov arrival process, allowing for dependent matrix-exponential distributed inter-arrival times. The processes were first characterised by Asmussen and Bladt and are referred to as rational arrival processes because the inter-arrival times have a rational Laplace–Stieltjes transform. Software Q-MAMa MATLAB MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation ... toolbox which can solve queueing systems with RAP arrivals. References Queueing theory {{probability-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Theory
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang when he created models to describe the system of Copenhagen Telephone Exchange company, a Danish company. The ideas have since seen applications including telecommunication, traffic engineering, computing and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is ''Queueing Systems''. Single queueing nodes A queue, or queueing no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |