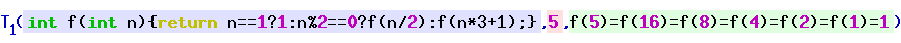|
M-recursive Function
In mathematical logic and computer science, a general recursive function, partial recursive function, or μ-recursive function is a partial function from natural numbers to natural numbers that is "computable" in an intuitive sense – as well as in a formal one. If the function is total, it is also called a total recursive function (sometimes shortened to recursive function). In computability theory, it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machines (this is one of the theorems that supports the Church–Turing thesis). The μ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every total recursive function is a primitive recursive function—the most famous example is the Ackermann function. Other equivalent classes of functions are the functions of lambda calculus and the functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logic
Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics. Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and analysis. In the early 20th century it was shaped by David Hilbert's program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to the program, and clarified the issues involved in proving consistency. Work in set theory s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
μ Operator
In computability theory, the μ-operator, minimization operator, or unbounded search operator searches for the least natural number with a given property. Adding the μ-operator to the five primitive recursive operators makes it possible to define all computable functions. Definition Suppose that R(''y'', ''x''1, ..., ''x''''k'') is a fixed (''k''+1)-ary relation on the natural numbers. The μ-operator "μ''y''", in either the unbounded or bounded form, is a "number theoretic function" defined from the natural numbers to the natural numbers. However, "μ''y''" contains a '' predicate'' over the natural numbers that delivers ''true'' when the predicate is satisfied and ''false'' when it is not. The ''bounded'' μ-operator appears earlier in Kleene (1952) ''Chapter IX Primitive Recursive Functions, §45 Predicates, prime factor representation'' as: :"\mu y_ R(y). \ \ \mbox \ y [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Turing Machine
In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input to that machine from its own tape. Alan Turing introduced the idea of such a machine in 1936–1937. This principle is considered to be the origin of the idea of a stored-program computer used by John von Neumann in 1946 for the "Electronic Computing Instrument" that now bears von Neumann's name: the von Neumann architecture.Martin Davis, ''The universal computer : the road from Leibniz to Turing'' (2017) In terms of computational complexity, a multi-tape universal Turing machine need only be slower by logarithmic factor compared to the machines it simulates. Introduction Every Turing machine computes a certain fixed partial computable function from the input strings over its alphabet. In that sense it b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marvin Minsky
Marvin Lee Minsky (August 9, 1927 – January 24, 2016) was an American cognitive and computer scientist concerned largely with research of artificial intelligence (AI), co-founder of the Massachusetts Institute of Technology's AI laboratory, and author of several texts concerning AI and philosophy. Minsky received many accolades and honors, including the 1969 Turing Award. Biography Marvin Lee Minsky was born in New York City, to an eye surgeon father, Henry, and to a mother, Fannie (Reiser), who was a Zionist activist. His family was Jewish. He attended the Ethical Culture Fieldston School and the Bronx High School of Science. He later attended Phillips Academy in Andover, Massachusetts. He then served in the US Navy from 1944 to 1945. He received a B.A. in mathematics from Harvard University in 1950 and a Ph.D. in mathematics from Princeton University in 1954. His doctoral dissertation was titled "Theory of neural-analog reinforcement systems and its application to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene's T Predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic. Informally, the ''T'' predicate tells whether a particular computer program will halt when run with a particular input, and the corresponding ''U'' function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.The predicate described here was presented in (Kleene 1943) and (Kleene 1952), and this is what is usually called "Kleene's ''T'' predicate". (Kleene 1967) uses the letter ''T'' to describe a different predicate related to computable functions, but which cannot be used to obtain Kleene's normal form theorem. Definition The definition depends on a suitable Gödel numbering that assigns natural numbers to computab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Church's Thesis
Church's is a high-end footwear manufacturer that was founded in 1873, by Thomas Church, in Northampton, England. In 1999 the company came under the control of Italian luxury fashion house Prada in a US$170 million deal. History Between the two world wars, Church's became actively involved in the development of the footwear industry in general. In 1919, the British Boot, Shoe and Allied Trades Research Association was created with Church's as a founder-member. As a result of this partnership, the Northampton Technical College was established in 1925. This went on to become the University of Northampton in 2005. The family business was taken over by Prada in 1999, in a US$170 million deal, and has since expanded its outlets overseas. In 2014 the company employed 650 people. The same year, Church's took over adjacent premises in St James Road, formerly a tram and later a bus depot, in anticipation of further expansion which was expected to create up to 140 more jobs. Some h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halting Problem
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever. Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program–input pairs cannot exist. For any program that might determine whether programs halt, a "pathological" program , called with some input, can pass its own source and its input to ''f'' and then specifically do the opposite of what ''f'' predicts ''g'' will do. No ''f'' can exist that handles this case. A key part of the proof is a mathematical definition of a computer and program, which is known as a Turing machine; the halting problem is '' undecidable'' over Turing machines. It is one of the first cases of decision problems proven to be unsolvable. This proof is significant to practical computing efforts, defining a class of applications which no programming inven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Turing Machine
In computability theory, a decider is a Turing machine that halts for every input. A decider is also called a total Turing machineKozen, 1997 as it represents a total function. Because it always halts, such a machine is able to decide whether a given string is a member of a formal language. The class of languages which can be decided by such machines is the set of recursive languages. Given an arbitrary Turing machine, determining whether it is a decider is an undecidable problem. This is a variant of the halting problem, which asks for whether a Turing machine halts on a specific input. Functions computable by total Turing machines In practice, many functions of interest are computable by machines that always halt. A machine that uses only finite memory on any particular input can be forced to halt for every input by restricting its flow control capabilities so that no input will ever cause the machine to enter an infinite loop. As a trivial example, a machine implementin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Junctor
A junctor is a circuit used in analog telephone exchanges, including the Number One Crossbar Switching System, Number Five Crossbar Switching System, 1ESS switch and other switches. In early electromechanical switches, a "district junctor" handled supervision and talk battery duties for outgoing calls, similar to the duties of the cord circuit of manual exchanges. The junctors for incoming calls were simple three-wire connections between the incoming frame and the line frame. In the later electromechanical 5XB switch, junctors only consisted of three wires to connect the two legs of a call: the line and the trunk, of which the latter supplied all talk battery and supervision. Stored-program analog switches such as the 1ESS switch, had both simple wire junctors and circuit junctors. Circuit junctors were in the form of plug-in circuit boards to provide talk battery and supervision for intraoffice calls and were closely similar to intraoffice trunk packs, with two scan points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Negation
In logic, negation, also called the logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P or \overline. It is interpreted intuitively as being true when P is false, and false when P is true. Negation is thus a unary logical connective. It may be applied as an operation on notions, propositions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes ''truth'' to ''falsity'' (and vice versa). In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition P is the proposition whose proofs are the refutations of P. Definition ''Classical negation'' is an operation on one logical value, typically the value of a proposition, that produces a value of ''true'' when its operand is false, and a value of ''false'' when its operand is true. Thus if statement is true, then \neg P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Square Root
In number theory, the integer square root (isqrt) of a non-negative integer ''n'' is the non-negative integer ''m'' which is the greatest integer less than or equal to the square root of ''n'', : \mbox( n ) = \lfloor \sqrt n \rfloor. For example, \mbox(27) = \lfloor \sqrt \rfloor = \lfloor 5.19615242270663 ... \rfloor = 5. Introductory remark Let y \text k be non-negative integers. Algorithms that compute (the decimal representation of) \sqrt y run forever on each input y which is not a perfect square. Algorithms that compute \lfloor \sqrt y \rfloor do not run forever. They are nevertheless capable of computing \sqrt y up to any desired accuracy k. Choose any k and compute \lfloor \sqrt \rfloor. For example (setting y = 2): :\begin & k = 0: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 1 \\ & k = 1: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 14 \\ & k = 2: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 141 \\ & k = 3: \lfloor \sqrt \rfloor = \lfloor \sqrt \r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive Function
In computability theory, a primitive recursive function is roughly speaking a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop can be determined before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not that easy to devise a computable function that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |