|
Long Wavelength Limit
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats. It is the distance between consecutive corresponding points of the same phase (waves), phase on the wave, such as two adjacent crests, troughs, or zero crossings, and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The multiplicative inverse, inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter ''lambda'' (λ). The term ''wavelength'' is also sometimes applied to modulation, modulated waves, and to the sinusoidal envelope (mathematics), envelopes of modulated waves or waves formed by Interference (wave propagation), interference of several sinusoids. Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wavelength
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted simply as \sin \theta and \cos \theta. More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and lig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the brain. Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of to . Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges. Acoustics Acoustics is the interdisciplinary science that deals with the study of mechanical waves in gasses, liquids, and solids including vibration, sound, ultrasound, and infrasound. A scientist who works in the field of acoustics is an ''acoustician'', while someone working in the field of acoustica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
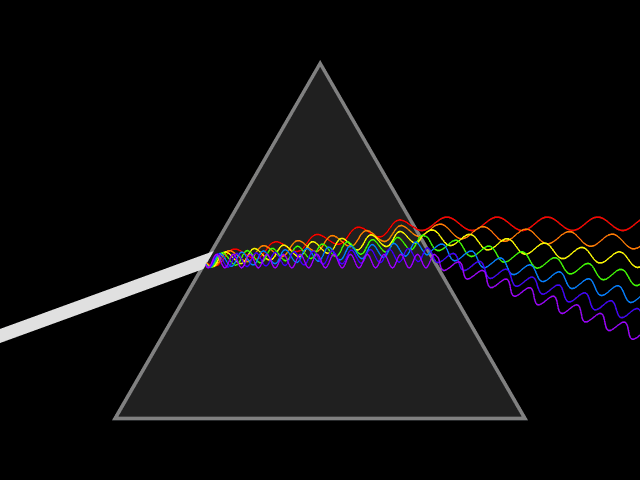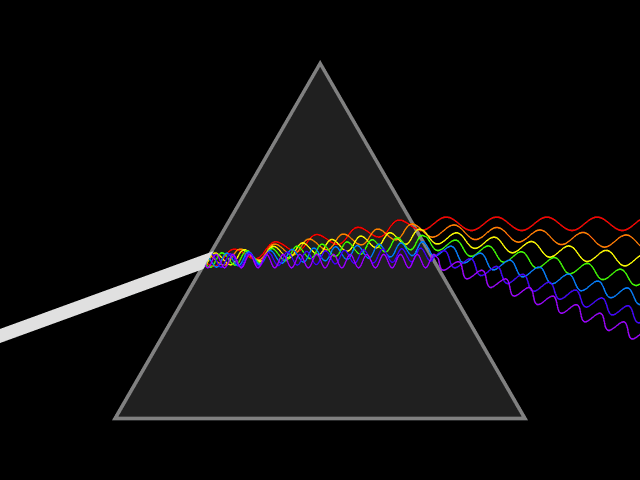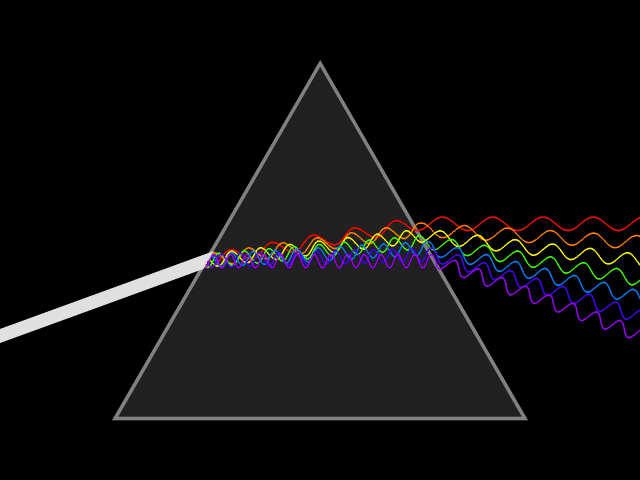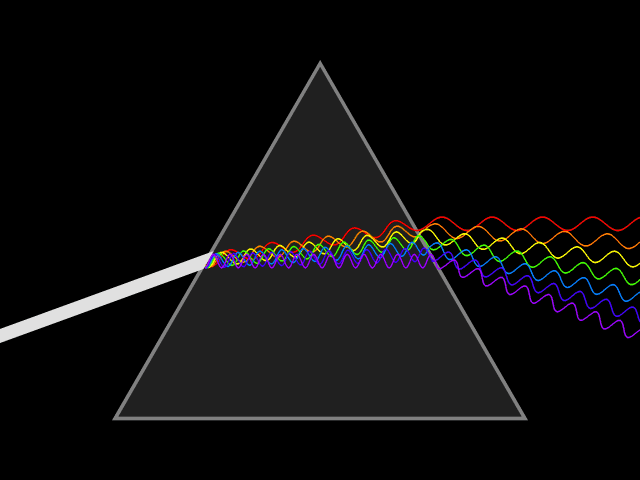
Dispersive Medium
In optics, and by analogy other branches of physics dealing with wave propagation, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular. A medium having this common property may be termed a dispersive medium (plural ''dispersive media''). Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the pulses of light in optical fiber. Physically, dispersion translates in a loss of kinetic energy through absorption. In optics, one important and familiar consequence of dispersion is the change in the angle of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength (lambda) and time period as :v_\mathrm = \frac. Equivalently, in terms of the wave's angular frequency , which specifies angular change per unit of time, and wavenumber (or angular wave number) , which represent the angular change per unit of space, :v_\mathrm = \frac. To gain some basic intuition for this equation, we consider a propagating (cosine) wave . We want to see how fast a particular phase of the wave travels. For example, we can choose , the phase of the first crest. This implies , and so . Formally, we let the phase and see immediately that and . So, it immediately follows that : \frac = -\frac \frac = \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor (Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily a real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibration Spectrum
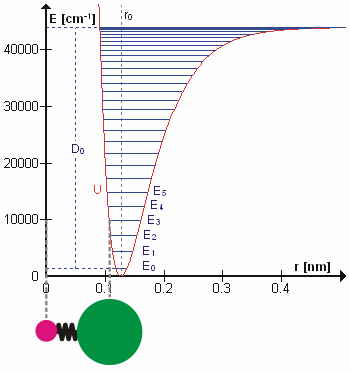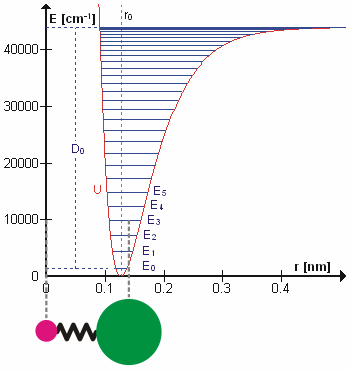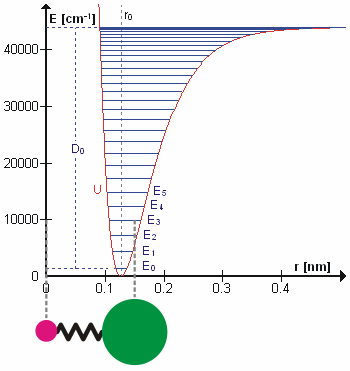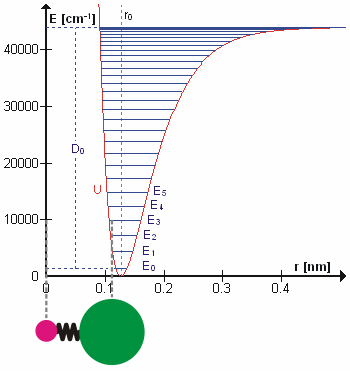
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 µm. For a diatomic molecule A−B, the vibrational frequency in s−1 is given by \nu = \frac \sqrt , where k is the force constant in dyne/cm or erg/cm2 and μ is the reduced mass given by \frac = \frac+\frac. The vibrational wavenumber in cm−1 is \tilde \;= \frac \sqrt, where c is the speed of light in cm/s. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of different parts of the molecule. In general, a non-linear molecule with ''N'' atoms has 3''N'' – 6 normal modes of vibration, but a ''linear'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound Spectrum
In the physical sciences, the term ''spectrum'' was introduced first into optics by Isaac Newton in the 17th century, referring to the range of colors observed when white light was dispersed through a prism. Soon the term referred to a plot of light intensity or power as a function of frequency or wavelength, also known as a ''spectral density plot''. Later it expanded to apply to other waves, such as sound waves and sea waves that could also be measured as a function of frequency (e.g., noise spectrum, sea wave spectrum). It has also been expanded to more abstract "signals", whose power spectrum can be analyzed and processed. The term now applies to any signal that can be measured or decomposed along a continuous variable, such as energy in electron spectroscopy or mass-to-charge ratio in mass spectrometry. Spectrum is also used to refer to a graphical representation of the signal as a function of the dependent variable. Electromagnetic spectrum Electromagnetic spectrum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Spectrum
The electromagnetic spectrum is the range of frequencies (the spectrum) of electromagnetic radiation and their respective wavelengths and photon energies. The electromagnetic spectrum covers electromagnetic waves with frequencies ranging from below one hertz to above 1025 hertz, corresponding to wavelengths from thousands of kilometers down to a fraction of the size of an atomic nucleus. This frequency range is divided into separate bands, and the electromagnetic waves within each frequency band are called by different names; beginning at the low frequency (long wavelength) end of the spectrum these are: radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays at the high-frequency (short wavelength) end. The electromagnetic waves in each of these bands have different characteristics, such as how they are produced, how they interact with matter, and their practical applications. There is no known limit for long and short wavelengths. Extreme ultr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
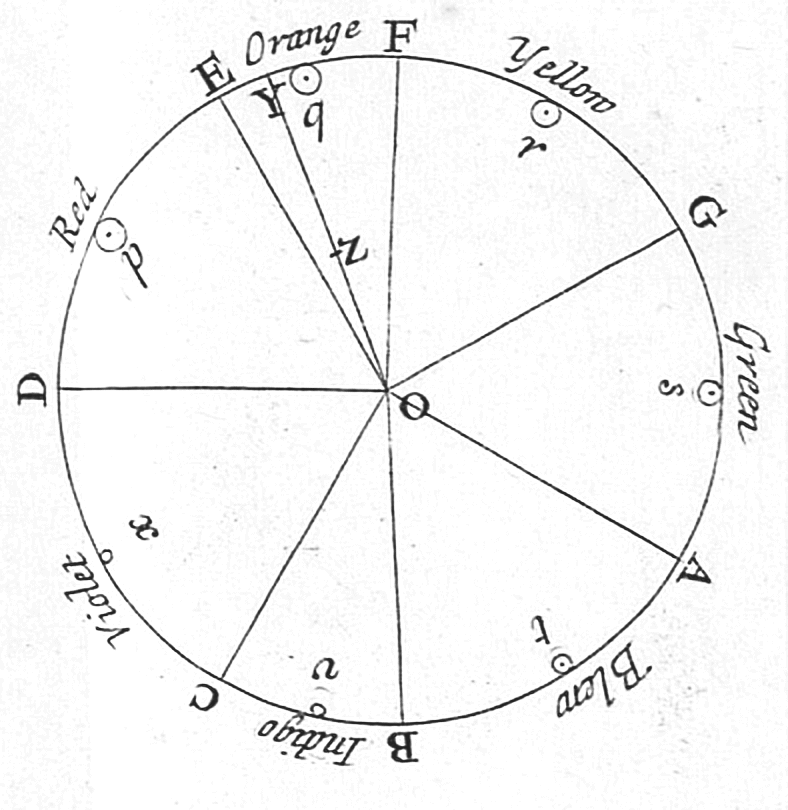
Visible Spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visual perception, visible to the human eye. Electromagnetic radiation in this range of wavelengths is called ''visible light'' or simply light. A typical human eye will respond to wavelengths from about 380 to about 750 nanometers. In terms of frequency, this corresponds to a band in the vicinity of 400–790 Terahertz (unit), terahertz. These boundaries are not sharply defined and may vary per individual. Under optimal conditions these limits of human perception can extend to 310 nm (ultraviolet) and 1100 nm (near infrared). The optical spectrum is sometimes considered to be the same as the visible spectrum, but some authors define the term more broadly, to include the ultraviolet and infrared parts of the electromagnetic spectrum as well. The spectrum does not contain all the colors that the human visual system can distinguish. ''Excitation purity, Unsaturated colors'' such as pink, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectrum
A spectrum (plural ''spectra'' or ''spectrums'') is a condition that is not limited to a specific set of values but can vary, without gaps, across a continuum. The word was first used scientifically in optics to describe the rainbow of colors in visible light after passing through a prism. As scientific understanding of light advanced, it came to apply to the entire electromagnetic spectrum. It thereby became a mapping of a range of magnitudes (wavelengths) to a range of qualities, which are the perceived "colors of the rainbow" and other properties which correspond to wavelengths that lie outside of the visible light spectrum. Spectrum has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the "autism spectrum". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of condition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Vibration
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name ''phonon'' comes from the Greek word (), which translates to ''sound'' or ''voice'', because long-wavelength phonons give rise to sound. The name is analogous to the word ''photon''. Definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)