Spectrum

A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics to describe the rainbow of colors in visible light after passing through a prism. In the optical spectrum, light wavelength is viewed as continuous, and spectral colors are seen to blend into one another smoothly when organized in order of their corresponding wavelengths. As scientific understanding of light advanced, the term came to apply to the entire electromagnetic spectrum, including radiation not visible to the human eye.

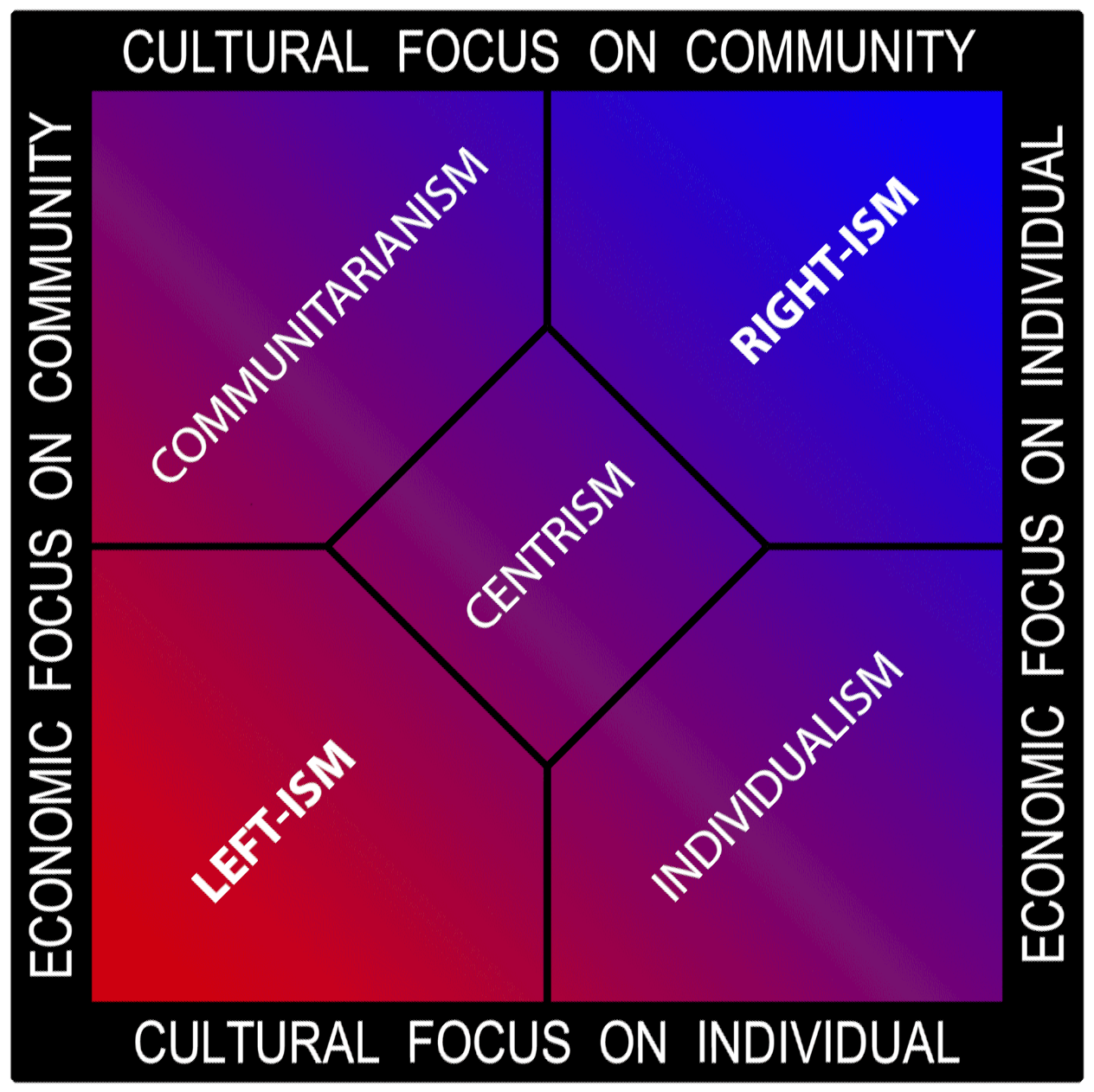
''Spectrum'' has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the " autism spectrum". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of conditions or behaviors grouped together and studied under a single title for ease of discussion. Nonscientific uses of the term ''spectrum'' are sometimes misleading. For instance, a single left–right spectrum of political opinion does not capture the full range of people's political beliefs. Political scientists use a variety of biaxial and multiaxial systems to more accurately characterize political opinion.

In most modern usages of ''spectrum'' there is a unifying theme between the extremes at either end. This was not always true in older usage.

Etymology

In Latin, ''spectrum'' means "image" or " apparition", including the meaning " spectre". Spectral evidence is testimony about what was done by spectres of persons not present physically, or hearsay evidence about what ghosts or apparitions of Satan said. It was used to convict a number of persons of witchcraft at Salem, Massachusetts in the late 17th century. The word "spectrum" pektrumwas strictly used to designate a ghostly optical afterimage by Goethe in his '' Theory of Colors'' and Schopenhauer in '' On Vision and Colors''.

The prefix "spectro-" is used to form words relating to spectra. For example, a spectrometer is a device used to record spectra and spectroscopy is the use of a spectrometer for chemical analysis.

Physical sciences

Biological science

Antibiotic spectrum of activity is a component of antibiotic classification. A broad-spectrum antibiotic is active against a wide range of bacteria, whereas a narrow-spectrum antibiotic is effective against specific families of bacteria.S.J. Hopkins, Drugs and Pharmacology for Nurses 12th ed., 1997 () An example of a commonly used broad-spectrum antibiotic is ampicillin. An example of a narrow spectrum antibiotic is Dicloxacillin, which acts on beta-lactamase-producing Gram-positive bacteria such as '' Staphylococcus aureus''.

In psychiatry, the spectrum approach uses the term spectrum to describe a range of linked conditions, sometimes also extending to include singular symptoms and traits. For example, the autism spectrum describes a range of conditions classified as neurodevelopmental disorders.

Mathematics

In mathematics, the spectrum of a matrix is the multiset of the eigenvalues of the matrix.

In functional analysis, the concept of the spectrum of a bounded operator is a generalization of the eigenvalue concept for matrices.

In algebraic topology, a spectrum is an object representing a generalized cohomology theory.

Social science

In social science, economic spectrum is used to indicate the range of social class along some indicator of wealth or income. In political science, the term political spectrum refers to a system of classifying political positions in one or more dimensions, for example in a range including right wing and left wing.

References

{{Authority control
Concepts in physics
Light
Broad-concept articles