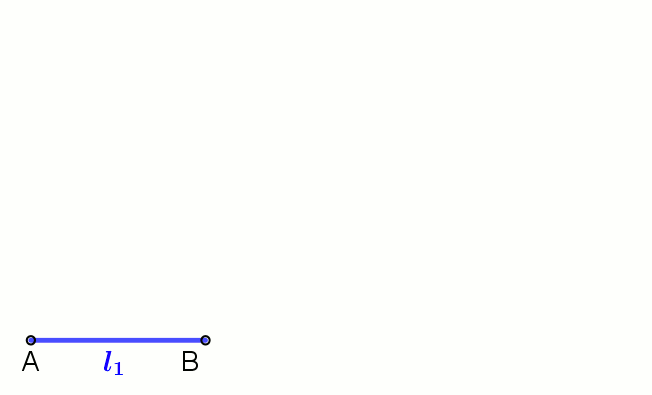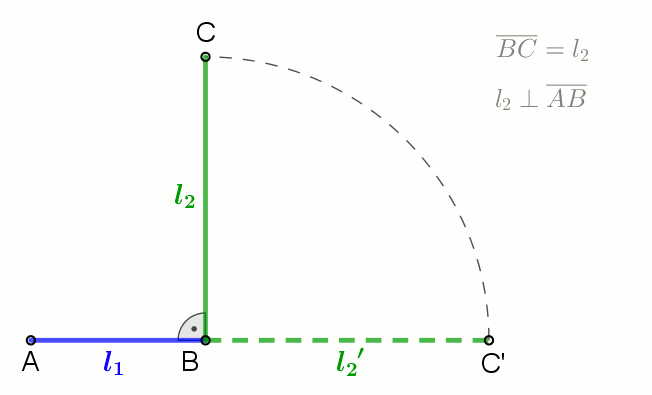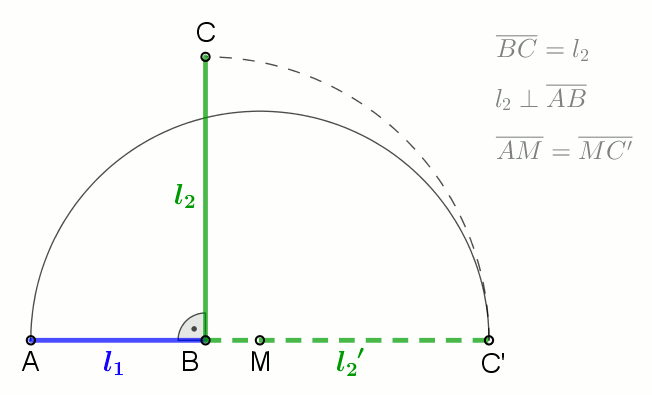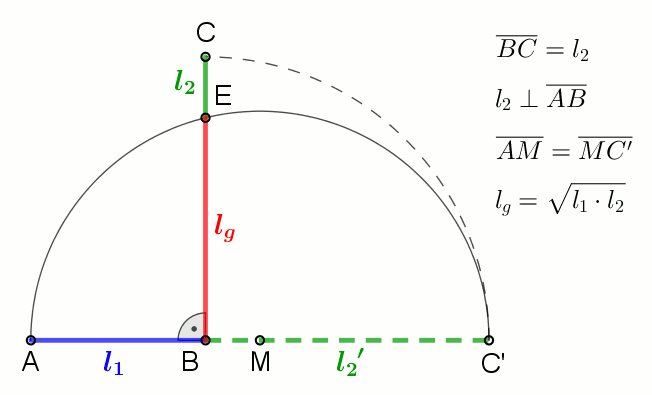|
List Of Operators
In mathematics, an operator or transform is a function from one space of functions to another. Operators occur commonly in engineering, physics and mathematics. Many are integral operators and differential operators. In the following ''L'' is an operator :L:\mathcal\to\mathcal which takes a function y\in\mathcal to another function L in\mathcal. Here, \mathcal and \mathcal are some unspecified function spaces, such as Hardy space, ''L''p space, Sobolev space, or, more vaguely, the space of holomorphic functions. {, class="wikitable" , - style="background:#eaeaea" ! style="text-align: center" , Expression ! style="text-align: center" , Curvedefinition ! style="text-align: center" , Variables ! style="text-align: center" , Description , - ! style="background:#eafaea" colspan=4, Linear transformations , - , L y^{(n)} , , , , , , Derivative of ''n''th order , - , L \int_a^t y \,dt , , Cartesian, , y=y(x)x=t, , Integral, area , - , L y\circ f, , , , , , Composition op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion Of Curves
Torsion may refer to: Science * Torsion (mechanics), the twisting of an object due to an applied torque * Torsion of spacetime, the field used in Einstein–Cartan theory and ** Alternatives to general relativity * Torsion angle, in chemistry Biology and medicine * Torsion fracture or spiral fracture, a bone fracture when torque is applied * Organ torsion, twisting that interrupts the blood supply to that organ: ** Splenic torsion, causing splenic infarction ** Ovarian torsion ** Testicular torsion * Penile torsion, a congenital condition * Torsion of the digestive tract in some domestic animals: ** Torsion, a type of horse colic ** Gastric torsion, or gastric dilatation volvulus * Torsion (gastropod), a developmental feature of all gastropods Mathematics * Torsion of a curve * Torsion tensor, in differential geometry * Torsion (algebra), in ring theory * Torsion group, in group theory and arithmetic geometry * Tor functor, the derived functors of the tensor product of modules ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Curvature
Special affine curvature, also known as the equiaffine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation (an affine transformation that preserves area). The curves of constant equiaffine curvature are precisely all non-singular plane conics. Those with are ellipses, those with are parabolae, and those with are hyperbolae. The usual Euclidean curvature of a curve at a point is the curvature of its osculating circle, the unique circle making second order contact (having three point contact) with the curve at the point. In the same way, the special affine curvature of a curve at a point is the special affine curvature of its hyperosculating conic, which is the unique conic making fourth order contact (having five point contact) with the curve at . In other words it is the limiting position of the (unique) conic through and four points on the curve, as each of the poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * Airport Regions Conference, a European organization of major airports * Amalgamated Roadstone Corporation, a British stone quarrying company * American Record Company (1904–1908, re-activated 1979), one of two United States record labels by this name * American Record Corporation (1929–1938), a United States record label also known as American Record Company * ARC (American Recording Company) (1978-present), a vanity label for Earth, Wind & Fire * ARC Document Solutions, a company based in California, formerly American Reprographics Company * Amey Roadstone Construction, a former British construction company * Aqaba Railway Corporation, a freight railway in Jordan * ARC/Architectural Resources Cambridge, Inc., Cambridge, Massachusett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subtangent
In geometry, the subtangent and related terms are certain line segments defined using the line tangent to a curve at a given point and the coordinate axes. The terms are somewhat archaic today but were in common use until the early part of the 20th century Definitions Let ''P'' = (''x'', ''y'') be a point on a given curve with ''A'' = (''x'', 0) its projection onto the ''x''-axis. Draw the tangent to the curve at ''P'' and let ''T'' be the point where this line intersects the ''x''-axis. Then ''TA'' is defined to be the subtangent at ''P''. Similarly, if normal to the curve at ''P'' intersects the ''x''-axis at ''N'' then ''AN'' is called the subnormal. In this context, the lengths ''PT'' and ''PN'' are called the tangent and normal, not to be confused with the tangent line and the normal line which are also called the tangent and normal. Equations Let ''φ'' be the angle of inclination of the tangent with respect to the ''x''-axis; this is also kno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Variation
In mathematics, the total variation identifies several slightly different concepts, related to the (local or global) structure of the codomain of a function or a measure. For a real-valued continuous function ''f'', defined on an interval 'a'', ''b''⊂ R, its total variation on the interval of definition is a measure of the one-dimensional arclength of the curve with parametric equation ''x'' ↦ ''f''(''x''), for ''x'' ∈ 'a'', ''b'' Functions whose total variation is finite are called functions of bounded variation. Historical note The concept of total variation for functions of one real variable was first introduced by Camille Jordan in the paper . He used the new concept in order to prove a convergence theorem for Fourier series of discontinuous periodic functions whose variation is bounded. The extension of the concept to functions of more than one variable however is not simple for various reasons. Definitions Total variation for functions of one real variable Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzian Derivative
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz. Definition The Schwarzian derivative of a holomorphic function of one complex variable is defined by : (Sf)(z) = \left( \frac\right)' - \frac\left(\right)^2 = \frac-\frac\left(\right)^2. The same formula also defines the Schwarzian derivative of a function of one real variable. The alternative notation :\ = (Sf)(z) is frequently used. Properties The Schwarzian derivative of any Möbius transformation : g(z) = \frac is zero. Conversely, the Möbius transformations are the only functions with this property. Thus, the Schwarzian der ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Of A Function
In mathematics, the elasticity or point elasticity of a positive differentiable function ''f'' of a positive variable (positive input, positive output) at point ''a'' is defined as :Ef(a) = \fracf'(a) :=\lim_\frac\frac=\lim_\frac\frac=\lim_\frac\approx \frac or equivalently :Ef(x) = \frac. It is thus the ratio of the relative (percentage) change in the function's output f(x) with respect to the relative change in its input x, for infinitesimal changes from a point (a, f(a)). Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. Generalisations to multi-input-multi-output cases also exist in the literature. The elasticity of a function is a constant \alpha if and only if the function has the form f(x) = C x ^ \alpha for a constant C>0. The elasticity at a point is the limit of the arc elasticity between two points as the separation between those two points approaches zero. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |