|
List Of Dynamical System Topics
This is a list of dynamical system and differential equation topics, by Wikipedia page. See also list of partial differential equation topics, list of equations. Dynamical systems, in general *Deterministic system (mathematics) *Linear system *Partial differential equation *Dynamical systems and chaos theory *Chaos theory ** Chaos argument ** Butterfly effect ** 0-1 test for chaos *Bifurcation diagram * Feigenbaum constant *Sharkovskii's theorem *Attractor **Strange nonchaotic attractor *Stability theory **Mechanical equilibrium **Astable ** Monostable **Bistability **Metastability *Feedback **Negative feedback **Positive feedback **Homeostasis *Damping ratio *Dissipative system *Spontaneous symmetry breaking *Turbulence *Perturbation theory *Control theory ** Non-linear control **Adaptive control ** Hierarchical control **Intelligent control ** Optimal control **Dynamic programming **Robust control ** Stochastic control *System dynamics, system analysis * Takens' theorem * Exponen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance. In dynamical systems, an orbit is called '' Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem invo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers. Turbulence is commonly observed in everyday phenomena such as surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices appear of many sizes which interact with each other, consequently drag due to friction effects increases. This increases the energy needed to pump fluid through a pipe. The onset of turbulence can be predicted by the dimensionless Rey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Symmetry Breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipative System
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter. A tornado may be thought of as a dissipative system. Dissipative systems stand in contrast to conservative systems. A dissipative structure is a dissipative system that has a dynamical regime that is in some sense in a reproducible steady state. This reproducible steady state may be reached by natural evolution of the system, by artifice, or by a combination of these two. Overview A dissipative structure is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. Examples in everyday life include convection, turbulent flow, cyclones, hurricanes and living organisms. Less common examples include lasers, Bénard cells, droplet cluster, and the Belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damping Ratio
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeostasis
In biology, homeostasis (British English, British also homoeostasis) Help:IPA/English, (/hɒmɪə(ʊ)ˈsteɪsɪs/) is the state of steady internal, physics, physical, and chemistry, chemical conditions maintained by organism, living systems. This is the condition of optimal functioning for the organism and includes many variables, such as body temperature and fluid balance, being kept within certain pre-set limits (homeostatic range). Other variables include the pH of extracellular fluid, the concentrations of sodium, potassium and calcium ions, as well as that of the blood sugar level, and these need to be regulated despite changes in the environment, diet, or level of activity. Each of these variables is controlled by one or more regulators or homeostatic mechanisms, which together maintain life. Homeostasis is brought about by a natural resistance to change when already in the optimal conditions, and equilibrium is maintained by many regulatory mechanisms: it is thought to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
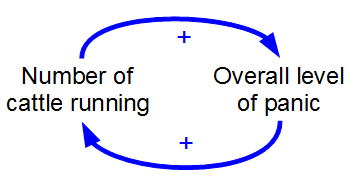
Positive Feedback
Positive feedback (exacerbating feedback, self-reinforcing feedback) is a process that occurs in a feedback loop which exacerbates the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, ''A produces more of B which in turn produces more of A''.Keesing, R.M. (1981). Cultural anthropology: A contemporary perspective (2nd ed.) p.149. Sydney: Holt, Rinehard & Winston, Inc. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics. Mathematically, positive feedback is defined as a positive loop gain around a closed loop of cause and effect. That is, positive feedback is in phase with the input, in the sense that it adds to make the input larger. Positive feedback tends to cause system instability. When the loop gain is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Feedback
Negative feedback (or balancing feedback) occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. Whereas positive feedback tends to lead to instability via exponential growth, oscillation or chaotic behavior, negative feedback generally promotes stability. Negative feedback tends to promote a settling to equilibrium, and reduces the effects of perturbations. Negative feedback loops in which just the right amount of correction is applied with optimum timing can be very stable, accurate, and responsive. Negative feedback is widely used in mechanical and electronic engineering, and also within living organisms, and can be seen in many other fields from chemistry and economics to physical systems such as the climate. General negative feedback systems are studied in control systems engineering. Negative feedback l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems: History Self-regulating mechanisms have existed since antiquity, and the idea of feedback had started to enter economic theory in Britain by the 18th century, but it was not at that time recognized as a universal abstraction and so did not have a name. The first ever known artificial feedback device was a float valve, for maintaining water at a constant level, invented in 270 BC in Alexandria, Egypt. This device illustrated the principle of feedback: a low water level opens the valve, the rising water then provides feedback into the system, closing the valve when the required level is reached. This then reoccurs in a circular fashion as the water level fluctuates. Centrifugal governors we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metastability
In chemistry and physics, metastability denotes an intermediate energetic state within a dynamical system other than the system's state of least energy. A ball resting in a hollow on a slope is a simple example of metastability. If the ball is only slightly pushed, it will settle back into its hollow, but a stronger push may start the ball rolling down the slope. Bowling pins show similar metastability by either merely wobbling for a moment or tipping over completely. A common example of metastability in science is isomerisation. Higher energy isomers are long lived because they are prevented from rearranging to their preferred ground state by (possibly large) barriers in the potential energy. During a metastable state of finite lifetime, all state-describing parameters reach and hold stationary values. In isolation: *the state of least energy is the only one the system will inhabit for an indefinite length of time, until more external energy is added to the system (unique "ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bistability
In a dynamical system, bistability means the system has two stable equilibrium states. Something that is bistable can be resting in either of two states. An example of a mechanical device which is bistable is a light switch. The switch lever is designed to rest in the "on" or "off" position, but not between the two. Bistable behavior can occur in mechanical linkages, electronic circuits, nonlinear optical systems, chemical reactions, and physiological and biological systems. In a conservative force field, bistability stems from the fact that the potential energy has two local minima, which are the stable equilibrium points. These rest states need not have equal potential energy. By mathematical arguments, a local maximum, an unstable equilibrium point, must lie between the two minima. At rest, a particle will be in one of the minimum equilibrium positions, because that corresponds to the state of lowest energy. The maximum can be visualized as a barrier between them. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> Spontaneous Symmetry Breaking")
