|
Lewis's Triviality Result
In the mathematical theory of probability, David Lewis's triviality result is a theorem about the impossibility of systematically equating the conditional probability P(B\mid A) with the probability of a so-called conditional event, A \rightarrow B. Conditional probability and conditional events The statement "The probability that if A, then B, is 20%" means (put intuitively) that event B may be expected to occur in 20% of the outcomes where event A occurs. The standard formal expression of this is P(B\mid A)=0.20, where the conditional probability P(B\mid A) equals, by definition, P(A \cap B)/P(A). Beginning in the 1960s, several philosophical logicians—most notably Ernest Adams and Robert Stalnaker—floated the idea that one might also write P(A \rightarrow B) = 0.20, where A \rightarrow B is the conditional event "If A, then B". That is, given events A and B, one might suppose there is an event, A \rightarrow B, such that P(A \rightarrow B) could be counted on to equal P( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Lewis (philosopher)
David Kellogg Lewis (September 28, 1941 – October 14, 2001) was an American philosopher who is widely regarded as one of the most important philosophers of the 20th century. Lewis taught briefly at UCLA and then at Princeton University from 1970 until his death. He is closely associated with Australia, whose philosophical community he visited almost annually for more than 30 years. Lewis made significant contributions in philosophy of mind, philosophy of probability, epistemology, philosophical logic, aesthetics, philosophy of mathematics, philosophy of time and philosophy of science. In most of these fields he is considered among the most important figures of recent decades. But Lewis is most famous for his work in metaphysics, philosophy of language and semantics, in which his books ''On the Plurality of Worlds'' (1986) and ''Counterfactuals'' (1973) are considered classics. His works on the logic and semantics of counterfactual conditionals are broadly used by philosop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bas Van Fraassen
Bastiaan Cornelis van Fraassen (; born 1941) is a Dutch-American philosopher noted for his contributions to philosophy of science, epistemology and formal logic. He is a Distinguished Professor of Philosophy at San Francisco State University and the McCosh Professor of Philosophy Emeritus at Princeton University. Biography and career Van Fraassen was born in the German-occupied Netherlands on 5 April 1941. His father, a steam fitter, was forced by the Nazis to work in a factory in Hamburg. After the war, the family reunited and, in 1956, emigrated to Edmonton, in western Canada. Van Fraassen earned his B.A. (1963) from the University of Alberta and his M.A. (1964) and Ph.D. (1966, under the direction of Adolf Grünbaum) from the University of Pittsburgh. He previously taught at Yale University, the University of Southern California, the University of Toronto and, from 1982 to 2008, at Princeton University, where he is now emeritus. Since 2008, van Fraassen has taught at San ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Articles Needing Expert Attention
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These conce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Event Algebra
A standard, Boolean algebra of events is a set of events related to one another by the familiar operations ''and'', ''or'', and ''not''. A conditional event algebra (CEA) contains not just ordinary events but also conditional events, which have the form "if ''A'', then ''B''". The usual purpose of a CEA is to enable the defining of a probability function, ''P'', that satisfies the equation ''P''(if ''A'' then ''B'') = ''P''(''A'' and ''B'') / ''P''(''A''). Motivation In standard probability theory, an event is a set of outcomes, any one of which would be an occurrence of the event. ''P''(''A''), the probability of event ''A'', is the sum of the probabilities of all ''A''-outcomes, ''P''(''B'') is the sum of the probabilities of all ''B''-outcomes, and ''P''(''A'' and ''B'') is the sum of the probabilities of all outcomes that are both ''A''-outcomes and ''B''-outcomes. In other words, ''and'', customarily represented by the logical symbol ∧, is interpreted as set intersection: ''P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Of Sets
In mathematics, the algebra of sets, not to be confused with the mathematical structure of ''an'' algebra of sets, defines the properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion. It also provides systematic procedures for evaluating expressions, and performing calculations, involving these operations and relations. Any set of sets closed under the set-theoretic operations forms a Boolean algebra with the join operator being ''union'', the meet operator being ''intersection'', the complement operator being ''set complement'', the bottom being \varnothing and the top being the universe set under consideration. Fundamentals The algebra of sets is the set-theoretic analogue of the algebra of numbers. Just as arithmetic addition and multiplication are associative and commutative, so are set union and intersection; just as the arithmetic relation "less than or equal" is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordered Pair
In mathematics, an ordered pair (''a'', ''b'') is a pair of objects. The order in which the objects appear in the pair is significant: the ordered pair (''a'', ''b'') is different from the ordered pair (''b'', ''a'') unless ''a'' = ''b''. (In contrast, the unordered pair equals the unordered pair .) Ordered pairs are also called 2-tuples, or sequences (sometimes, lists in a computer science context) of length 2. Ordered pairs of scalars are sometimes called 2-dimensional vectors. (Technically, this is an abuse of terminology since an ordered pair need not be an element of a vector space.) The entries of an ordered pair can be other ordered pairs, enabling the recursive definition of ordered ''n''-tuples (ordered lists of ''n'' objects). For example, the ordered triple (''a'',''b'',''c'') can be defined as (''a'', (''b'',''c'')), i.e., as one pair nested in another. In the ordered pair (''a'', ''b''), the object ''a'' is called the ''first entry'', and the object ''b'' the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radical Probabilism
Radical probabilism is a hypothesis in philosophy, in particular epistemology, and probability theory that holds that no facts are known for certain. That view holds profound implications for statistical inference. The philosophy is particularly associated with Richard Jeffrey who wittily characterised it with the ''dictum'' "It's probabilities all the way down." Background Bayes' theorem states a rule for updating a probability conditioned on other information. In 1967, Ian Hacking argued that in a static form, Bayes' theorem only connects probabilities that are held simultaneously; it does not tell the learner how to update probabilities when new evidence becomes available over time, contrary to what contemporary Bayesians suggested. According to Hacking, adopting Bayes' theorem is a temptation. Suppose that a learner forms probabilities ''P''old(''A'' & ''B'') = ''p'' and ''P''old(''B'') = ''q''. If the learner subsequently learns that ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagram Of Disjoint Events A And B, Together With The Conditional Event If A Or B, Then B
A diagram is a symbolic representation of information using visualization techniques. Diagrams have been used since prehistoric times on walls of caves, but became more prevalent during the Enlightenment. Sometimes, the technique uses a three-dimensional visualization which is then projected onto a two-dimensional surface. The word '' graph'' is sometimes used as a synonym for diagram. Overview The term "diagram" in its commonly used sense can have a general or specific meaning: * ''visual information device'' : Like the term "illustration", "diagram" is used as a collective term standing for the whole class of technical genres, including graphs, technical drawings and tables. * ''specific kind of visual display'' : This is the genre that shows qualitative data with shapes that are connected by lines, arrows, or other visual links. In science the term is used in both ways. For example, Anderson (1997) stated more generally: "diagrams are pictorial, yet abstract, represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
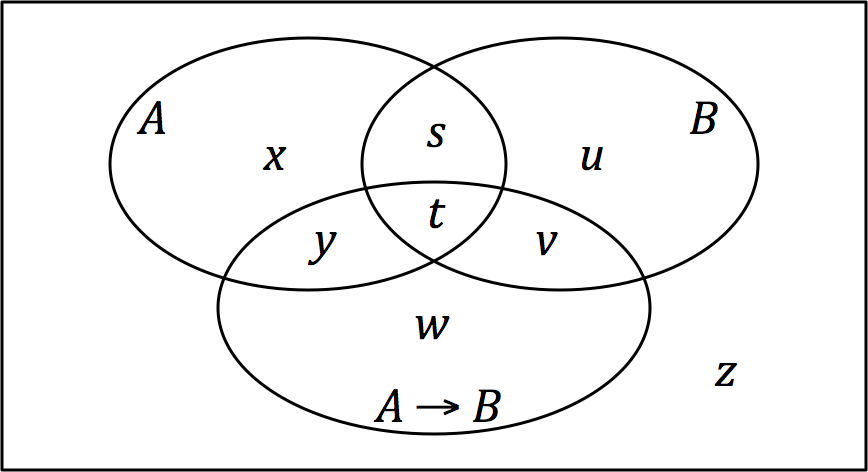
Venn Diagram Of Events A And B And The Conditional Event If A Then B
Venn is a surname and a given name. It may refer to: Given name * Venn Eyre (died 1777), Archdeacon of Carlisle, Cumbria, England * Venn Pilcher (1879–1961), Anglican bishop, writer, and translator of hymns * Venn Young (1929–1993), New Zealand politician Surname * Albert Venn (1867–1908), American lacrosse player * Anne Venn (1620s–1654), English religious radical and diarist * Blair Venn, Australian actor * Charles Venn (born 1973), British actor * Harry Venn (1844–1908), Australian politician * Henry Venn (Church Missionary Society) the younger (1796-1873), secretary of the Church Missionary Society, grandson of Henry Venn * Henry Venn (Clapham Sect) the elder (1725–1797), English evangelical minister * Horace Venn (1892–1953), English cricketer * John Venn (1834–1923), British logician and the inventor of Venn diagrams, son of Henry Venn the younger * John Venn (academic) (died 1687), English academic administrator * John Venn (politician) (1586–1650) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Axioms
The Kolmogorov axioms are the foundations of probability theory introduced by Russian mathematician Andrey Kolmogorov in 1933. These axioms remain central and have direct contributions to mathematics, the physical sciences, and real-world probability cases. An alternative approach to formalising probability, favoured by some Bayesians, is given by Cox's theorem. Axioms The assumptions as to setting up the axioms can be summarised as follows: Let (\Omega, F, P) be a measure space with P(E) being the probability of some event E'','' and P(\Omega) = 1. Then (\Omega, F, P) is a probability space, with sample space \Omega, event space F and probability measure P. First axiom The probability of an event is a non-negative real number: :P(E)\in\mathbb, P(E)\geq 0 \qquad \forall E \in F where F is the event space. It follows that P(E) is always finite, in contrast with more general measure theory. Theories which assign negative probability relax the first axiom. Second axiom This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Diagram
An Euler diagram (, ) is a diagrammatic means of representing sets and their relationships. They are particularly useful for explaining complex hierarchies and overlapping definitions. They are similar to another set diagramming technique, Venn diagrams. Unlike Venn diagrams, which show all possible relations between different sets, the Euler diagram shows only relevant relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler (1707–1783). In the United States, both Venn and Euler diagrams were incorporated as part of instruction in set theory as part of the new math movement of the 1960s. Since then, they have also been adopted by other curriculum fields such as reading as well as organizations and businesses. Euler diagrams consist of simple closed shapes in a two-dimensional plane that each depict a set or category. How or whether these shapes overlap demonstrates the relationships between the sets. Each curve divide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |