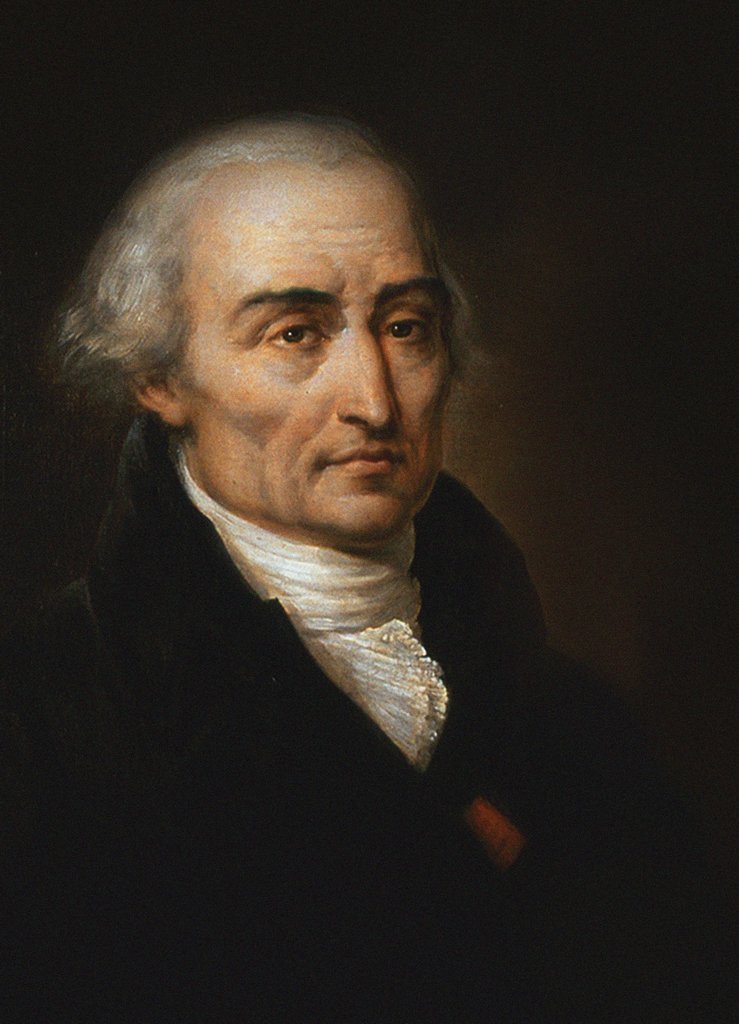|
Louis François Antoine Arbogast
Louis François Antoine Arbogast (4 October 1759 – 8 April 1803) was a French mathematician. He was born at Mutzig in Alsace and died at Strasbourg, where he was professor. He wrote on series and the derivatives known by his name: he was the first writer to separate the symbols of operation from those of quantity, introducing systematically the operator notation ''DF'' for the derivative of the function ''F''. In 1800, he published a calculus treatise where the first known statement of what is currently known as Faà di Bruno's formula appears, 55 years before the first published paper of Francesco Faà di Bruno on that topic. Biography He was professor of mathematics at the Collège de Colmar and entered a mathematical competition run by the St Petersburg Academy. His entry was to bring him fame and an important place in the history of the development of the calculus. Arbogast submitted an essay to the St Petersburg Academy in which he came down firmly on the side of Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutzig
Mutzig ( or ; german: Mützig) is a commune in the Bas-Rhin department in Grand Est, in north-eastern France. The commune of Mutzig is located at the entrance of the Bruche river valley, on the Route des Vins d'Alsace. History Evidences of human activities can be traced back to the Paleolithic era with the recent discovery of Neanderthal artifacts. The town Mutzig was first mentioned in the 10th century. It became part of the Prince-Bishopric of Strasbourg in 1308. In the 19th century, several industries were established in Mutzig among which a weapon manufactory on the grounds of the former castle of the . In 1893, when [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faà Di Bruno's Formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives. It is named after , although he was not the first to state or prove the formula. In 1800, more than 50 years before Faà di Bruno, the French mathematician Louis François Antoine Arbogast had stated the formula in a calculus textbook, which is considered to be the first published reference on the subject. Perhaps the most well-known form of Faà di Bruno's formula says that f(g(x))=\sum \frac\cdot f^(g(x))\cdot \prod_^n\left(g^(x)\right)^, where the sum is over all ''n''-tuples of nonnegative integers (''m''1, ..., ''m''''n'') satisfying the constraint 1\cdot m_1+2\cdot m_2+3\cdot m_3+\cdots+n\cdot m_n=n. Sometimes, to give it a memorable pattern, it is written in a way in which the coefficients that have the combinatorial interpretation discussed below are less explicit: : f(g(x)) =\sum \frac\cdot f^(g(x))\cdot \prod_^n\left(\frac\right)^. Combining the terms with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book '' Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential function an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace
Pierre-Simon, marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French scholar and polymath whose work was important to the development of engineering, mathematics, statistics, physics, astronomy, and philosophy. He summarized and extended the work of his predecessors in his five-volume ''Mécanique céleste'' (''Celestial Mechanics'') (1799–1825). This work translated the geometric study of classical mechanics to one based on calculus, opening up a broader range of problems. In statistics, the Bayesian interpretation of probability was developed mainly by Laplace. Laplace formulated Laplace's equation, and pioneered the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplacian differential operator, widely used in mathematics, is also named after him. He restated and developed the nebular hypothesis of the origin of the Solar System and was one of the first scientists to suggest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an and , later naturalized [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Series
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence (a_0, a_1, a_2, \ldots) defines a series that is denoted :S=a_0 +a_1+ a_2 + \cdots=\sum_^\infty a_k. The th partial sum is the sum of the first terms of the sequence; that is, :S_n = \sum_^n a_k. A series is convergent (or converges) if the sequence (S_1, S_2, S_3, \dots) of its partial sums tends to a limit; that means that, when adding one a_k after the other ''in the order given by the indices'', one gets partial sums that become closer and closer to a given number. More precisely, a series converges, if there exists a number \ell such that for every arbitrarily small positive number \varepsilon, there is a (sufficiently large) integer N such that for all n \ge N, :\left , S_n - \ell \right , 1 produce a convergent series: *: ++++++\cdots = . * Alternating the signs of reciprocals of powers of 2 also produces a convergent series: *: -+-+-+\cdots = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Académie Des Sciences
The French Academy of Sciences (French: ''Académie des sciences'') is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research. It was at the forefront of scientific developments in Europe in the 17th and 18th centuries, and is one of the earliest Academies of Sciences. Currently headed by Patrick Flandrin (President of the Academy), it is one of the five Academies of the Institut de France. History The Academy of Sciences traces its origin to Colbert's plan to create a general academy. He chose a small group of scholars who met on 22 December 1666 in the King's library, near the present-day Bibliothèque Nationals, and thereafter held twice-weekly working meetings there in the two rooms assigned to the group. The first 30 years of the Academy's existence were relatively informal, since no statutes had as yet been laid down for the institution. In contrast to its British ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: "More concepts and theorems have been named for Cauchy than for any other mathematician (in Elasticity (physics), elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discontinuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
St Petersburg
Saint Petersburg ( rus, links=no, Санкт-Петербург, a=Ru-Sankt Peterburg Leningrad Petrograd Piter.ogg, r=Sankt-Peterburg, p=ˈsankt pʲɪtʲɪrˈburk), formerly known as Petrograd (1914–1924) and later Leningrad (1924–1991), is the second-largest city in Russia. It is situated on the Neva River, at the head of the Gulf of Finland on the Baltic Sea, with a population of roughly 5.4 million residents. Saint Petersburg is the fourth-most populous city in Europe after Istanbul, Moscow and London, the most populous city on the Baltic Sea, and the world's northernmost city of more than 1 million residents. As Russia's Imperial capital, and a historically strategic port, it is governed as a federal city. The city was founded by Tsar Peter the Great on 27 May 1703 on the site of a captured Swedish fortress, and was named after apostle Saint Peter. In Russia, Saint Petersburg is historically and culturally associated with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Laplace")
