|
Log Wind Profile
The log wind profile is a semi-empirical relationship commonly used to describe the vertical distribution of horizontal mean wind speed within the lowest portion of the planetary boundary layer (PBL). The logarithmic profile of wind speeds is generally limited to the lowest 100 m of the atmosphere (i.e., the surface layer of the atmospheric boundary layer). The rest of the atmosphere is composed of the remaining part of the PBL (up to around 1 km) and the troposphere or free atmosphere. In the free atmosphere, geostrophic wind relationships should be used, instead. Formulation The equation to estimate the mean wind speed (u_z) at height z (meters) above the ground is: :u_z = \frac \left ln \left(\frac \right) + \psi(z,z_0,L)\right/math> where u_* is the friction velocity (m s−1), \kappa is the Von Kármán constant (~0.41), d is the zero plane displacement (in metres), z_0 is the surface roughness (in meters), and \psi is a stability term where L is the Obukhov length from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Position
Vertical position or vertical location is a position (mathematics), position along a vertical direction (the plumb line direction) above or below a given vertical datum (a reference level surface, such as mean sea level). Vertical distance or vertical separation is the distance between two vertical positions. Many vertical coordinates exist for expressing vertical position: depth, height, altitude, elevation, etc. Points lying on an equigeopotential surface are said to be on the same vertical level, as in a water level (device), water level. A function (mathematics), function with domain (mathematics), domain along the vertical line is called a ''vertical distribution'' or ''vertical profile''. Definitions The International Organization for Standardization (ISO), more specifically Spatial reference system, ISO 19111, offers the following two definitions: * ''depth'': "distance of a point from a chosen reference surface measured downward along a line perpendicular to that surface." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
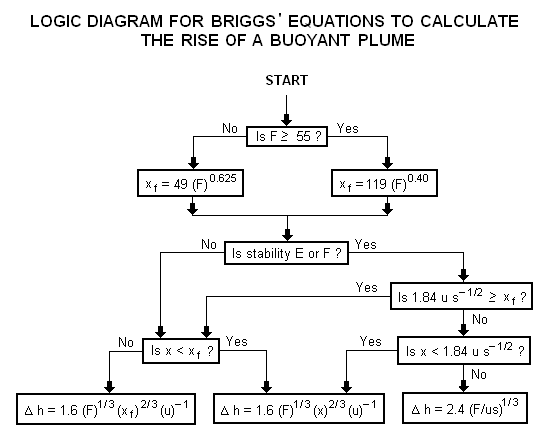
Air Pollution Dispersion Terminology
The following outline is provided as an overview of and topical guide to air pollution dispersion: In environmental science, air pollution dispersion is the distribution of air pollution into the atmosphere. ''Air pollution'' is the introduction of particulates, biological molecules, or other harmful materials into Earth's atmosphere, causing disease, death to humans, damage to other living organisms such as food crops, and the natural or built environment. Air pollution may come from anthropogenic or natural sources. ''Dispersion'' refers to what happens to the pollution during and after its introduction; understanding this may help in identifying and controlling it. Air pollution dispersion has become the focus of environmental conservationists and governmental environmental protection agencies (local, state, province and national) of many countries (which have adopted and used much of the terminology of this field in their laws and regulations) regarding air pollution contr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Layer Meteorology
Boundary or Boundaries may refer to: * Border, in political geography Entertainment * ''Boundaries'' (2016 film), a 2016 Canadian film * ''Boundaries'' (2018 film), a 2018 American-Canadian road trip film *Boundary (cricket), the edge of the playing field, or a scoring shot where the ball is hit to or beyond that point * Boundary (sports), the sidelines of a field * ''Boundary'' (video game), a defunct 2023 multiplayer video game set in outre space Mathematics and physics *Boundary (topology), the closure minus the interior of a subset of a topological space; an edge in the topology of manifolds, as in the case of a 'manifold with boundary' * Boundary (graph theory), the vertices of edges between a subgraph and the rest of a graph * Boundary (chain complex), its abstractization in chain complexes *Boundary value problem, a differential equation together with a set of additional restraints called the boundary conditions * Boundary (thermodynamics), the edge of a thermodynamic syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Dispersion Modeling
Atmospheric dispersion modeling is the mathematical simulation of how air pollutants disperse in the ambient atmosphere. It is performed with computer programs that include algorithms to solve the mathematical equations that govern the pollutant dispersion. The dispersion models are used to estimate the downwind ambient concentration of air pollutants or toxins emitted from sources such as industrial plants, vehicular traffic or accidental chemical releases. They can also be used to predict future concentrations under specific scenarios (i.e. changes in emission sources). Therefore, they are the dominant type of model used in air quality policy making. They are most useful for pollutants that are dispersed over large distances and that may react in the atmosphere. For pollutants that have a very high spatio-temporal variability (i.e. have very steep distance to source decay such as black carbon) and for epidemiological studies statistical land-use regression models are also u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Atmospheric Dispersion Models
Atmospheric dispersion models are computer programs that use mathematical algorithms to simulate how pollutants in the ambient atmosphere disperse and, in some cases, how they react in the atmosphere. US Environmental Protection Agency models Many of the dispersion models developed by or accepted for use by the U.S. Environmental Protection Agency (U.S. EPA) are accepted for use in many other countries as well. Those EPA models are grouped below into four categories. Preferred and recommended models * AERMOD – An atmospheric dispersion model based on atmospheric boundary layer turbulence structure and scaling concepts, including treatment of multiple ground-level and elevated point, area and volume sources. It handles flat or complex, rural or urban terrain and includes algorithms for building effects and plume penetration of inversions aloft. It uses Gaussian dispersion for stable atmospheric conditions (i.e., low turbulence) and non-Gaussian dispersion for unstable co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind Profile Power Law
The wind profile power law is a relationship between the wind speeds at one height, and those at another. Definition The wind profile power law relationship is :\frac = \bigg(\frac \bigg)^\alpha where u is the wind speed (in metres per second) at height z (in metres), and u_r is the known wind speed at a reference height z_r. The exponent (\alpha) is an empirically derived coefficient that varies dependent upon the stability of the atmosphere. For neutral stability conditions, \alpha is approximately 1/7, or 0.143. In order to estimate the wind speed at a certain height ''z'', the relationship would be rearranged to :u = u_r\bigg(\frac \bigg)^\alpha The value of 1/7 for α is commonly assumed to be constant in wind resource assessments, because the differences between the two levels are not usually so great as to introduce substantial errors into the estimates (usually < 50 m). However, when a constant exponent is used, it does not account for the roughness of the surface, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Dispersion Modeling
Atmospheric dispersion modeling is the mathematical simulation of how air pollutants disperse in the ambient atmosphere. It is performed with computer programs that include algorithms to solve the mathematical equations that govern the pollutant dispersion. The dispersion models are used to estimate the downwind ambient concentration of air pollutants or toxins emitted from sources such as industrial plants, vehicular traffic or accidental chemical releases. They can also be used to predict future concentrations under specific scenarios (i.e. changes in emission sources). Therefore, they are the dominant type of model used in air quality policy making. They are most useful for pollutants that are dispersed over large distances and that may react in the atmosphere. For pollutants that have a very high spatio-temporal variability (i.e. have very steep distance to source decay such as black carbon) and for epidemiological studies statistical land-use regression models are also u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind Profile Power Law
The wind profile power law is a relationship between the wind speeds at one height, and those at another. Definition The wind profile power law relationship is :\frac = \bigg(\frac \bigg)^\alpha where u is the wind speed (in metres per second) at height z (in metres), and u_r is the known wind speed at a reference height z_r. The exponent (\alpha) is an empirically derived coefficient that varies dependent upon the stability of the atmosphere. For neutral stability conditions, \alpha is approximately 1/7, or 0.143. In order to estimate the wind speed at a certain height ''z'', the relationship would be rearranged to :u = u_r\bigg(\frac \bigg)^\alpha The value of 1/7 for α is commonly assumed to be constant in wind resource assessments, because the differences between the two levels are not usually so great as to introduce substantial errors into the estimates (usually < 50 m). However, when a constant exponent is used, it does not account for the roughness of the surface, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roughness Length
Roughness length (z_0) is a parameter used in modeling the horizontal mean wind speed near the ground. In wind vertical profile such the log wind profile, the roughness length (with dimension of length and SI unit of metres) is equivalent to the height at which the wind speed theoretically becomes zero in the absence of wind-slowing obstacles and under neutral conditions. In reality, the wind at this height no longer follows a logarithm. It is so named because it is typically related to the height of terrain roughness elements (i.e. protrusions from and/or depressions into the surface). For instance, forests tend to have much larger roughness lengths than tundra. The roughness length does not exactly correspond to any physical length; however, it can be considered as a length-scale representation of the roughness of the surface. Mathematical foundation The roughness length z_0 appears in the expression for the mean wind speed u_z near the ground derived using the Monin–Obukhov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
