|
List Of Spherical Symmetry Groups
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry. This article lists the groups by Schoenflies notation, Coxeter notation, orbifold notation, and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion. Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.Sands, "Introduction to Crystallography", 1993 Involutional symmetry There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group (mathematics), group of all isometry, isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrix, orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetry, symmetries. All isometries of a Bounded set, bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the Origin (mathematics), origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with Euclidean group#Direct and indirect is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold Notation
In geometry, orbifold notation (or orbifold signature) is a system, invented by the mathematician William Thurston and promoted by John Horton Conway, John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration. Groups representable in this notation include the point groups in three dimensions, point groups on the sphere (S^2), the frieze groups and wallpaper groups of the Euclidean plane (E^2), and their analogues on the hyperbolic geometry, hyperbolic plane (H^2). Definition of the notation The following types of Euclidean transformation can occur in a group described by orbifold notation: * reflection through a line (or plane) * translation by a vector * rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Symmetry Group C2v
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the n-gon, -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition The word "dihedral" comes from "di-" and "-hedron". The latter comes from the Greek word hédra, which means "face of a geometrical solid". Overall it thus refers to the two faces of a polygon. Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetry, rotational symmetries and n reflection symmetry, reflection symmetries. Usually, we take n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Symmetry Group C2h
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
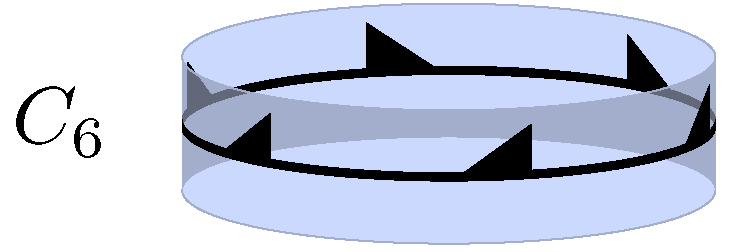
Cyclic Symmetries
In three dimensional geometry, there are four infinite series of point groups in three dimensions (''n''≥1) with ''n''-fold rotational or reflectional symmetry about one axis (by an angle of 360°/''n'') that does not change the object. They are the finite symmetry groups on a cone. For ''n'' = ∞ they correspond to four frieze groups. Schönflies notation is used. The terms horizontal (h) and vertical (v) imply the existence and direction of reflections with respect to a vertical axis of symmetry. Also shown are Coxeter notation in brackets, and, in parentheses, orbifold notation. Types ;Chiral: *''Cn'', sup>+, (''nn'') of order ''n'' - ''n''-fold rotational symmetry - acro-n-gonal group (abstract group ''Zn''); for ''n''=1: no symmetry (trivial group) ;Achiral: *''Cnh'', +,2 (''n''*) of order 2''n'' - prismatic symmetry or ortho-n-gonal group (abstract group ''Zn'' × ''Dih1''); for ''n''=1 this is denoted by ''Cs'' (1*) and called reflection symmetry, also bilatera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Symmetry Group Cs
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, generated by a single element. That is, it is a set (mathematics), set of Inverse element, invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer Exponentiation, power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a ''Generating set of a group, generator'' of the group. Every infinite cyclic group is isomorphic to the additive group \Z, the integers. Every finite cyclic group of Order (group theory), order n is isomorphic to the additive group of Quotient group, Z/''n''Z, the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
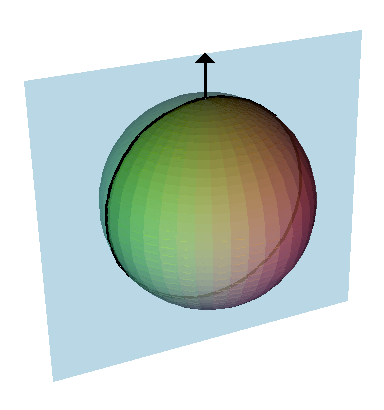
Sphere Symmetry Group C1
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |