|
List Of Polyhedral Stellations
In the geometry of three-dimensional space, three dimensions, a stellation extends a polyhedron to form a new figure that is also a polyhedron. The following is a list of stellations of various polyhedra. See also * List of Wenninger polyhedron models * The Fifty-Nine Icosahedra Footnotes References * * * {{DEFAULTSORT:Polyhedral stellations Polyhedral stellation, Mathematics-related lists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First Compound Stellation Of Icosahedron
First or 1st is the ordinal form of the number one (#1). First or 1st may also refer to: * World record, specifically the first instance of a particular achievement Arts and media Music * 1$T, American rapper, singer-songwriter, DJ, and record producer Albums * ''1st'' (album), a 1983 album by Streets * ''1st'' (Rasmus EP), a 1995 EP by The Rasmus, frequently identified as a single * '' 1ST'', a 2021 album by SixTones * ''First'' (Baroness EP), an EP by Baroness * ''First'' (Ferlyn G EP), an EP by Ferlyn G * ''First'' (David Gates album), an album by David Gates * ''First'' (O'Bryan album), an album by O'Bryan * ''First'' (Raymond Lam album), an album by Raymond Lam * ''First'', an album by Denise Ho Songs * "First" (Cold War Kids song), a song by Cold War Kids * "First" (Lindsay Lohan song), a song by Lindsay Lohan * "First", a song by Everglow from ''Last Melody'' * "First", a song by Lauren Daigle * "First", a song by Niki & Gabi * "First", a song by Jonas Br ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Great Icosahedron And Stellated Dodecahedron
Compound may refer to: Architecture and built environments * Compound (enclosure), a cluster of buildings having a shared purpose, usually inside a fence or wall ** Compound (fortification), a version of the above fortified with defensive structures * Compound (migrant labour), a hostel for migrant workers such as those historically connected with mines in South Africa * The Compound, an area of Palm Bay, Florida, US * Komboni or compound, a type of slum in Zambia Government and law * Composition (fine), a legal procedure in use after the English Civil War ** Committee for Compounding with Delinquents, an English Civil War institution that allowed Parliament to compound the estates of Royalists * Compounding treason, an offence under the common law of England * Compounding a felony, a previous offense under the common law of England Linguistics * Compound (linguistics), a word that consists of more than one radical element * Compound sentence (linguistics), a type of sentence ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
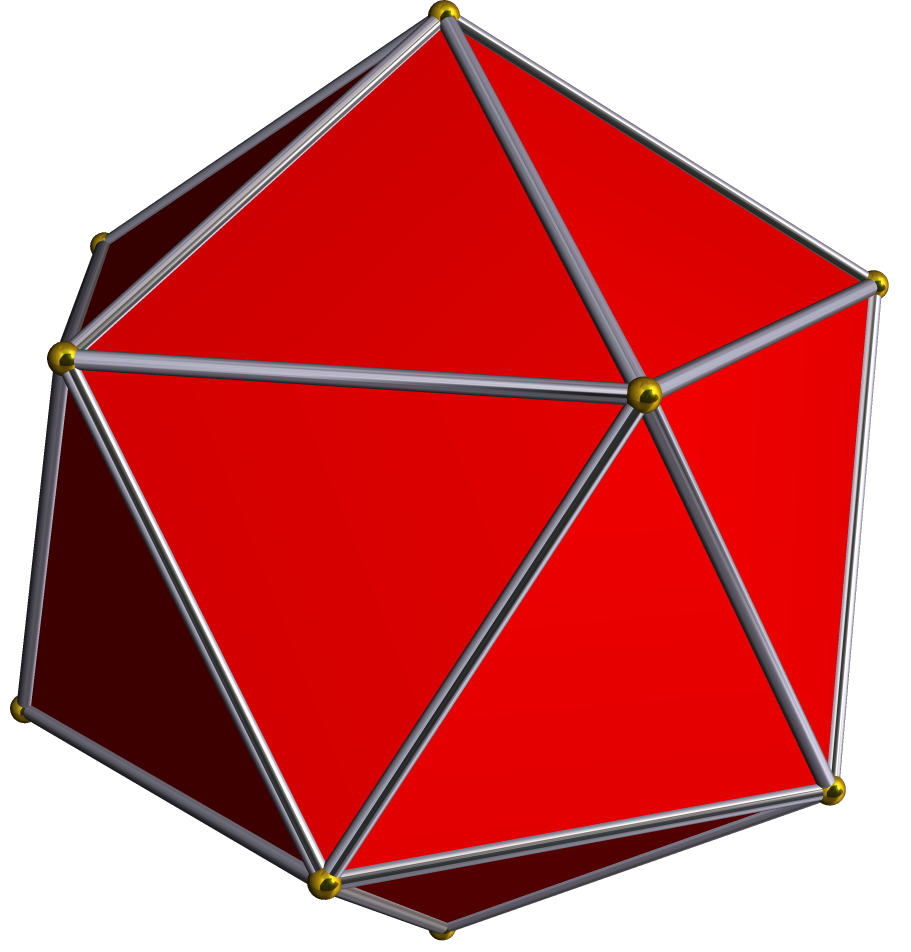
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty (''icosi'') triangular faces and twelve (''dodeca'') pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron. Geometry An icosidodecahedron has icosahedral symmetry, and its first stellation is the compound of a dodecahedron and its dual icosahedron, with the vertices of the icosidodecahedron located at the midpoints of the edges of either. Its dual polyhedron is the rhombic triacontahedron. An icosidodecahedron can be split along any of six planes to form a pair of pentagonal rotundae, which belong among the Johnson solids. The icosidodecahedron can be considered a ''pentagonal gyrobirotunda'', as a combination of two rotundae (compare pentagonal orthobirotunda, one of the Johnson solids) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Great Icosahedron And Great Stellated Dodecahedron
There are two different compounds of great icosahedron and great stellated dodecahedron: one is a dual compound and a stellation of the great icosidodecahedron, the other is a stellation of the icosidodecahedron. Dual compound It can be seen as a polyhedron compound of a great icosahedron and great stellated dodecahedron. It is one of five compounds constructed from a Platonic solid or Kepler-Poinsot solid, and its dual. It is a stellation of the great icosidodecahedron. It has icosahedral symmetry (I''h'') and it has the same vertex arrangement as a great rhombic triacontahedron. This can be seen as one of the two three-dimensional equivalents of the compound of two pentagrams ( " decagram"); this series continues into the fourth dimension as compounds of star 4-polytopes. Stellation of the icosidodecahedron This polyhedron is a stellation of the icosidodecahedron, and given as Wenninger model index 61. It has the same vertex arrangement as a rhombic triacontahedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Compound Stellation Of Icosidecahedron
The second (symbol: s) is the unit of time in the International System of Units (SI), historically defined as of a day – this factor derived from the division of the day first into 24 hours, then to 60 minutes and finally to 60 seconds each (24 × 60 × 60 = 86400). The current and formal definition in the International System of Units ( SI) is more precise:The second ..is defined by taking the fixed numerical value of the caesium frequency, Δ''ν''Cs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be when expressed in the unit Hz, which is equal to s−1. This current definition was adopted in 1967 when it became feasible to define the second based on fundamental properties of nature with caesium clocks. Because the speed of Earth's rotation varies and is slowing ever so slightly, a leap second is added at irregular intervals to civil time to keep clocks in sync with Earth's rotation. Uses Analog clocks and watches often have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Triacontahedron
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron. The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, , so that the acute angles on each face measure or approximately 63.43°. A rhombus so obtained is called a ''golden rhombus''. Being the dual of an Archimedean solid, the rhombic triacontahedron is ''face-transitive'', meaning the symmetry group of the solid acts transitively on the set of faces. This means that for any two faces, and , there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face to face . The rhombic triacontahedron is somewhat special in being one of the nine edge-transitive c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Cubes
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876. It is one of five regular compounds, and dual to the compound of five octahedra. It can be seen as a faceting of a regular dodecahedron. It is one of the stellations of the rhombic triacontahedron. It has icosahedral symmetry (Ih). Geometry The compound is a faceting of a dodecahedron (where pentagrams can be seen correlating to the pentagonal faces). Each cube represents a selection of 8 of the 20 vertices of the dodecahedron. If the shape is considered as a union of five cubes yielding a simple nonconvex solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182 − 540 + 360 = 2. Edge arrangement Its convex hull is a regular dodecahedron. It additionally shares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Triambic Icosahedron
In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical Dual polyhedron, dual uniform polyhedra. The exterior surface also represents the The Fifty-Nine Icosahedra, De2f2 Great_triambic_icosahedron#As_a_stellation, stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true Vertex (geometry), vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ. The 12 vertices of the convex hull matches the vertex arrangement of an icosahedron. Great triambic icosahedron The great triambic icosahedron is the dual of the great ditrigonal icosidodecahedron, U47. It has 20 inverted-hexagonal (triambus) faces, shaped like a three-bladed propeller. It has 32 vertices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
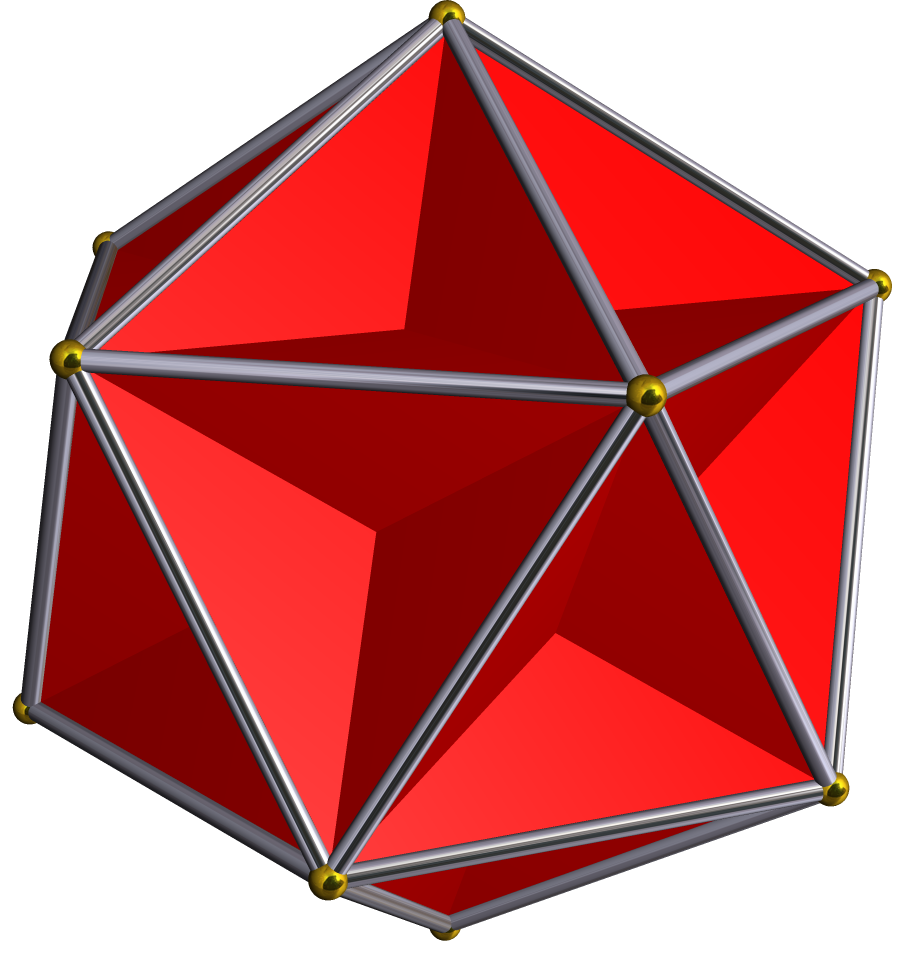
Stellation Icosahedron De2f2
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word ''stellation'' comes from the Latin ''stellātus'', "starred", which in turn comes from Latin ''stella'', "star". Stellation is the reciprocal or dual process to '' faceting''. Kepler's definition In 1619 Kepler defined stellation for polygons and polyhedra as the process of extending edges or faces until they meet to form a new polygon or polyhedron. He stellated the regular dodecahedron to obtain two regular star polyhedra, the small stellated dodecahedron and great stellated dodecahedron. He also stellated the regular octa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Triambic Icosahedron
In geometry, the small triambic icosahedron is a star polyhedron composed of 20 intersecting non-regular hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8. It is an isohedron, meaning that all of its faces are symmetric to each other. Branko Grünbaum has conjectured that it is the only Euclidean isohedron with convex faces of six or more sides, but the small hexagonal hexecontahedron is another example. Geometry The faces are equilateral hexagons, with alternating angles of \arccos(-\frac)\approx 104.477\,512\,185\,93^ and \arccos(\frac)+60^\approx 135.522\,487\,814\,07^. The dihedral angle equals \arccos(-\frac)\approx 109.471\,220\,634\,49. Related shapes The external surface of the small triambic icosahedron (removing the parts of each hexagonal face that are surrounded by other faces, but interpreting the resulting disconnected plane figures as still being faces) coincides with one of the stellations of the icosahedron. (1st Edn Unive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First Stellation Of Icosahedron
In geometry, the small triambic icosahedron is a star polyhedron composed of 20 intersecting non-regular hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8. It is an isohedron, meaning that all of its faces are symmetric to each other. Branko Grünbaum has conjectured that it is the only Euclidean isohedron with convex faces of six or more sides, but the small hexagonal hexecontahedron is another example. Geometry The faces are equilateral hexagons, with alternating angles of \arccos(-\frac)\approx 104.477\,512\,185\,93^ and \arccos(\frac)+60^\approx 135.522\,487\,814\,07^. The dihedral angle equals \arccos(-\frac)\approx 109.471\,220\,634\,49. Related shapes The external surface of the small triambic icosahedron (removing the parts of each hexagonal face that are surrounded by other faces, but interpreting the resulting disconnected plane figures as still being faces) coincides with one of the stellations of the icosahedron. (1st Edn Univers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |