|
List Of Scientific Equations Named After People ...
This is a list of scientific equations named after people (eponymous equations)."Reflections on the Natural History of Eponymy and Scientific Law", Donald deB. Beaver, ''Social Studies of Science'', volume 6, number 1 (February, 1976), pages 89–98 See also * Eponym * List of eponymous laws * List of laws in science * List of equations * Scientific constants named after people * Scientific phenomena named after people * Scientific laws named after people References {{reflist Equations named after people Scientific equations named after people Equations Equations In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adams–Williamson Equation
The Adams–Williamson equation, named after Leason H. Adams and E. D. Williamson, is an equation used to determine density as a function of radius, more commonly used to determine the relation between the velocities of seismic waves and the density of the Earth's interior. Given the average density of rocks at the Earth's surface and profiles of the P-wave and S-wave speeds as function of depth, it can predict how density increases with depth. It assumes that the compression is adiabatic and that the Earth is spherically symmetric, homogeneous, and in hydrostatic equilibrium. It can also be applied to spherical shells with that property. It is an important part of models of the Earth's interior such as the Preliminary reference Earth model (PREM). History Williamson and Adams first developed the theory in 1923. They concluded that "It is therefore impossible to explain the high density of the Earth on the basis of compression alone. The dense interior cannot consist of ord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bateman Equation
In nuclear physics, the Bateman equation is a mathematical model describing abundances and activities in a decay chain as a function of time, based on the decay rates and initial abundances. The model was formulated by Ernest Rutherford in 1905 and the analytical solution was provided by Harry Bateman in 1910. If, at time ''t'', there are N_i(t) atoms of isotope i that decays into isotope i+1 at the rate \lambda_i, the amounts of isotopes in the ''k''-step decay chain evolves as: : \begin \frac & =-\lambda_1 N_1(t) \\ pt\frac & =-\lambda_i N_i(t) + \lambda_N_(t) \\ pt\frac & = \lambda_N_(t) \end (this can be adapted to handle decay branches). While this can be solved explicitly for ''i'' = 2, the formulas quickly become cumbersome for longer chains. The Bateman equation is a classical master equation where the transition rates are only allowed from one species (i) to the next (i+1) but never in the reverse sense (i+1 to i is forbidden). Bateman found a general expl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Differential Equation
In mathematics, an ordinary differential equation is called a Bernoulli differential equation if it is of the form : y'+ P(x)y = Q(x)y^n, where n is a real number. Some authors allow any real n, whereas others require that n not be 0 or 1. The equation was first discussed in a work of 1695 by Jacob Bernoulli, after whom it is named. The earliest solution, however, was offered by Gottfried Leibniz, who published his result in the same year and whose method is the one still used today. Bernoulli equations are special because they are nonlinear differential equations with known exact solutions. A notable special case of the Bernoulli equation is the logistic differential equation. Transformation to a linear differential equation When n = 0, the differential equation is linear. When n = 1, it is separable. In these cases, standard techniques for solving equations of those forms can be applied. For n \neq 0 and n \neq 1, the substitution u = y^ reduces any Bernoulli equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Bernoulli
Daniel Bernoulli FRS (; – 27 March 1782) was a Swiss mathematician and physicist and was one of the many prominent mathematicians in the Bernoulli family from Basel. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. His name is commemorated in the Bernoulli's principle, a particular example of the conservation of energy, which describes the mathematics of the mechanism underlying the operation of two important technologies of the 20th century: the carburetor and the airplane wing. Early life Daniel Bernoulli was born in Groningen, in the Netherlands, into a family of distinguished mathematicians.Rothbard, MurrayDaniel Bernoulli and the Founding of Mathematical Economics ''Mises Institute'' (excerpted from '' An Austrian Perspective on the History of Economic Thought'') The Bernoulli family came originally from Antwerp, at that time in the Spanish Neth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
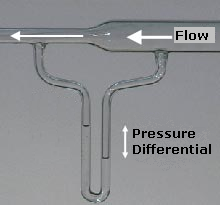
Bernoulli's Equation
In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book ''Hydrodynamica'' in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form. The principle is only applicable for isentropic flows: when the effects of irreversible processes (like turbulence) and non-adiabatic processes (e.g. thermal radiation) are small and can be neglected. Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation. The simple form of Bernoulli's equation is valid for incompressible flows (e.g. most liquid flows and gases moving at low Mach number). More advanced forms may be applied ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerry L
Jerry may refer to: Animals * Jerry (Grand National winner), racehorse, winner of the 1840 Grand National * Jerry (St Leger winner), racehorse, winner of 1824 St Leger Stakes Arts, entertainment, and media * ''Jerry'' (film), a 2006 Indian film * "Jerry", a song from the album ''Young and Free'' by Rock Goddess * Tom and Jerry (other) People * Jerry (given name), including a list of people and fictional characters with the name * Harold A. Jerry, Jr. (1920–2001), New York politician * Thomas Jeremiah (d. 1775), commonly known simply as "Jerry", a free Negro in colonial South Carolina Places * Branche à Jerry, a tributary of the Baker River in Quebec and New Brunswick, Canada * Jerry, Washington, a community in the United States Other uses * Jerry (company) * Jerry (WWII), Allied nickname for Germans, originally from WWI but widely used in World War II * Jerry Rescue (1851), involving American slave William Henry, who called himself "Jerry" See also * Geri (disa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brooke Benjamin
Thomas Brooke Benjamin, FRS (15 April 1929 – 16 August 1995) was an English mathematical physicist and mathematician, best known for his work in mathematical analysis and fluid mechanics, especially in applications of nonlinear differential equations. Education and career Benjamin was educated at Wallasey Grammar School on the Wirral, the University of Liverpool (BEng. 1950) and Yale University (MEng. 1952), before being awarded his doctorate at King's College, Cambridge in 1955. He was a fellow of King's from 1955 to 1964. From 1979 until his death in 1995 he was Sedleian Professor of Natural Philosophy at the Mathematical Institute, University of Oxford, and a fellow of The Queen's College, Oxford. Contributions The Benjamin–Ono equation describes one-dimensional internal waves in deep water. It was introduced by Benjamin in 1967, and later studied also by Hiroaki Ono. Another equation named after Benjamin, the Benjamin–Bona–Mahony equation, models long surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benjamin–Ono Equation
In mathematics, the Benjamin–Ono equation is a nonlinear partial integro-differential equation that describes one-dimensional internal waves in deep water. It was introduced by and . The Benjamin–Ono equation is :u_t+uu_x+Hu_=0 where ''H'' is the Hilbert transform. See also * Bretherton equation In mathematics, the Bretherton equation is a nonlinear partial differential equation introduced by Francis Bretherton in 1964: :u_+u_+u_+u = u^p, with p integer and p \ge 2. While u_t, u_x and u_ denote partial derivatives of the scalar field ... References * * External linksBenjamin-Ono equations: Solitons and Shock Waves Nonlinear partial differential equations Integrable systems {{theoretical-physics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benjamin–Bona–Mahony Equation
The Benjamin–Bona–Mahony equation (BBM equation, also regularized long-wave equation; RLWE) is the partial differential equation :u_t+u_x+uu_x-u_=0.\, This equation was studied in as an improvement of the Korteweg–de Vries equation (KdV equation) for modeling long surface gravity waves of small amplitude – propagating uni-directionally in 1+1 dimensions. They show the stability and uniqueness of solutions to the BBM equation. This contrasts with the KdV equation, which is unstable in its high wavenumber components. Further, while the KdV equation has an infinite number of integrals of motion, the BBM equation only has three. Before, in 1966, this equation was introduced by Peregrine, in the study of undular bores. A generalized ''n''-dimensional version is given by :u_t-\nabla^2u_t+\operatorname\,\varphi(u)=0.\, where \varphi is a sufficiently smooth function from \mathbb R to \mathbb R^n. proved global existence of a solution in all dimensions. Solitary wave ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benedict–Webb–Rubin Equation
The Benedict–Webb–Rubin equation (BWR), named after Manson Benedict, G. B. Webb, and L. C. Rubin, is an equation of state used in fluid dynamics. Working at the research laboratory of the M. W. Kellogg Company, the three researchers rearranged the Beattie–Bridgeman equation of state and increased the number of experimentally determined constants to eight. The original BWR equation :P=\rho RT + \left(B_0 RT-A_0 - \frac \right) \rho^2 + \left(bRT-a\right) \rho^3 + \alpha a \rho^6 + \frac\left(1 + \gamma\rho^2\right)\exp\left(-\gamma\rho^2\right), where \rho is the molar density Molar may refer to: *Molar (tooth), a kind of tooth found in mammals *Molar (grape), another name for the Spanish wine grape Listan Negro *Molar (unit), a unit of concentration equal to 1 mole per litre *Molar mass *Molar volume *El Molar, Tarragon .... The BWRS equation of state A modification of the Benedict–Webb–Rubin equation of state by Professor Kenneth E. Starling of the University of Ok ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Coordinates
In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifold are local coordinates where the metric is conformal to the Euclidean metric. This means that in isothermal coordinates, the Riemannian metric locally has the form : g = \varphi (dx_1^2 + \cdots + dx_n^2), where \varphi is a positive smooth function. (If the Riemannian manifold is oriented, some authors insist that a coordinate system must agree with that orientation to be isothermal.) Isothermal coordinates on surfaces were first introduced by Gauss. Korn and Lichtenstein proved that isothermal coordinates exist around any point on a two dimensional Riemannian manifold. By contrast, most higher-dimensional manifolds do not admit isothermal coordinates anywhere; that is, they are not usually locally conformally flat. In dimension 3, a Riemannian metric is locally conformally flat if and only if its Cotton tensor vanishes. In dimensions > 3, a metric is locally conformally fla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |