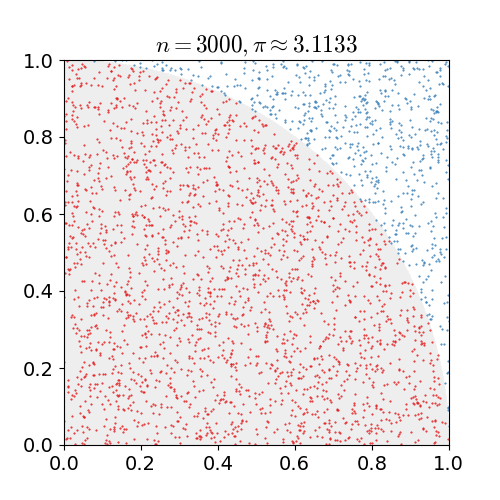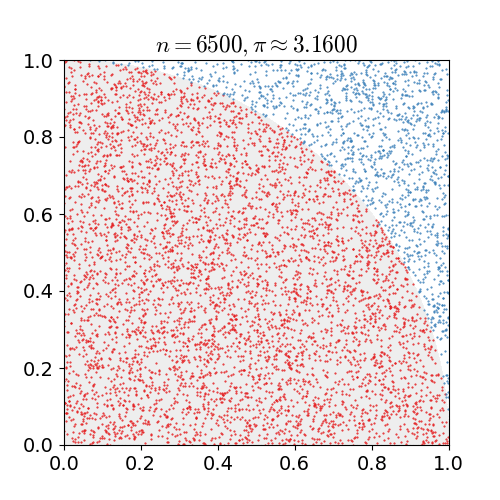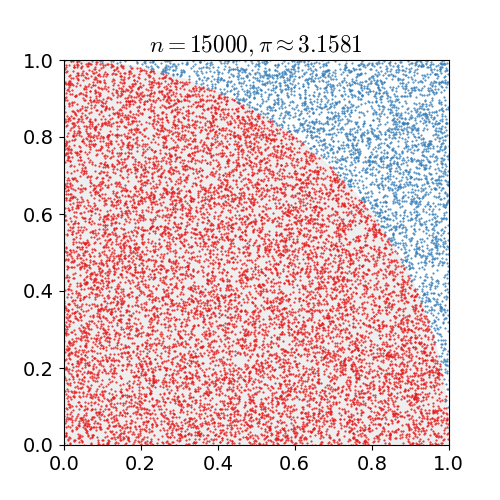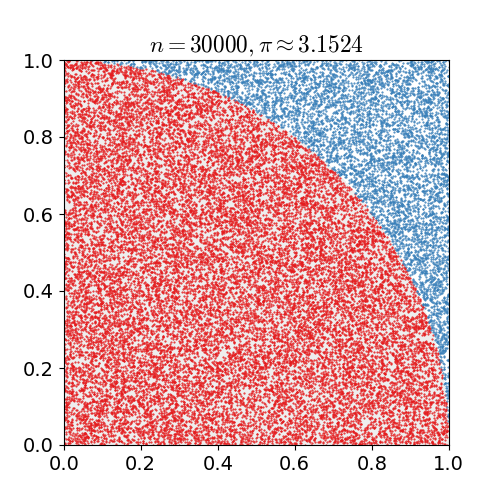
|
Lilliefors Test
In statistics, the Lilliefors test is a normality test based on the Kolmogorov–Smirnov test. It is used to test the null hypothesis that data come from a normally distributed population, when the null hypothesis does not specify ''which'' normal distribution; i.e., it does not specify the expected value and variance of the distribution. It is named after Hubert Lilliefors, professor of statistics at George Washington University. A variant of the test can be used to test the null hypothesis that data come from an exponentially distributed population, when the null hypothesis does not specify which exponential distribution. The test The test proceeds as follows: # First estimate the population mean and population variance based on the data. # Then find the maximum discrepancy between the empirical distribution function and the cumulative distribution function (CDF) of the normal distribution with the estimated mean and estimated variance. Just as in the Kolmogorov–Smirnov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by an ''upwards continuous'' ''monotonic increasing'' cumulative distribution function F : \mathbb R \rightarrow ,1/math> satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability that the random variable X takes on a value less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python (programming Language)
Python is a high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is dynamically-typed and garbage-collected. It supports multiple programming paradigms, including structured (particularly procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC programming language and first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000 and introduced new features such as list comprehensions, cycle-detecting garbage collection, reference counting, and Unicode support. Python 3.0, released in 2008, was a major revision that is not completely backward-compatible with earlier versions. Python 2 was discontinued with version 2.7.18 in 2020. Python consistently ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jarque–Bera Test
In statistics, the Jarque–Bera test is a goodness-of-fit test of whether sample data have the skewness and kurtosis matching a normal distribution. The test is named after Carlos Jarque and Anil K. Bera. The test statistic is always nonnegative. If it is far from zero, it signals the data do not have a normal distribution. The test statistic ''JB'' is defined as : \mathit = \frac \left( S^2 + \frac14 (K-3)^2 \right) where ''n'' is the number of observations (or degrees of freedom in general); ''S'' is the sample skewness, ''K'' is the sample kurtosis : : S = \frac = \frac , : K = \frac = \frac , where \hat_3 and \hat_4 are the estimates of third and fourth central moments, respectively, \bar is the sample mean, and \hat^2 is the estimate of the second central moment, the variance. If the data comes from a normal distribution, the ''JB'' statistic asymptotically has a chi-squared distribution with two degrees of freedom, so the statistic can be us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Order
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable A may be neither stochastically greater than, less than nor equal to another random variable B. Many different orders exist, which have different applications. Usual stochastic order A real random variable A is less than a random variable B in the "usual stochastic order" if :\Pr(A>x) \le \Pr(B>x)\textx \in (-\infty,\infty), where \Pr(\cdot) denotes the probability of an event. This is sometimes denoted A \preceq B or A \le_ B. If additionally \Pr(A>x) x) for some x, then A is stochastically strictly less than B, sometimes denoted A \prec B. In decision theory, under this circumstance ''B'' is said to be first-order stochastically dominant over ''A''. Characterizations The following rules describe situations when one random variable is stochastically less than or equal to another. Str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
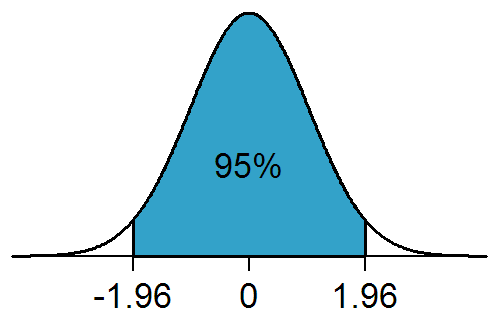
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Distribution Function
In statistics, an empirical distribution function (commonly also called an empirical Cumulative Distribution Function, eCDF) is the distribution function associated with the empirical measure of a sample. This cumulative distribution function is a step function that jumps up by at each of the data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value. The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution, according to the Glivenko–Cantelli theorem. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function. Definition Let be independent, identically distributed real random variables with the common cumulative distrib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normality Test
In statistics, normality tests are used to determine if a data set is well-modeled by a normal distribution and to compute how likely it is for a random variable underlying the data set to be normally distributed. More precisely, the tests are a form of model selection, and can be interpreted several ways, depending on one's interpretations of probability: * In descriptive statistics terms, one measures a goodness of fit of a normal model to the data – if the fit is poor then the data are not well modeled in that respect by a normal distribution, without making a judgment on any underlying variable. * In frequentist statistics statistical hypothesis testing, data are tested against the null hypothesis that it is normally distributed. * In Bayesian statistics, one does not "test normality" per se, but rather computes the likelihood that the data come from a normal distribution with given parameters ''μ'',''σ'' (for all ''μ'',''σ''), and compares that with the likelihood that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |