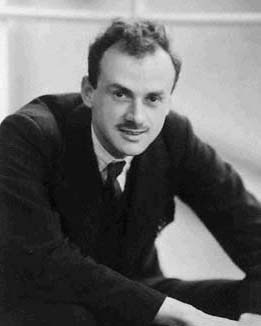|
Light Front Quantization
The light-front quantization of Quantum field theory, quantum field theories provides a useful alternative to ordinary equal-time Quantization (physics), quantization. In particular, it can lead to a Special relativity, relativistic description of Bound state, bound systems in terms of Quantum mechanics, quantum-mechanical wave functions. The quantization is based on the choice of light-front coordinates, where x^+\equiv ct+z plays the role of time and the corresponding spatial coordinate is x^-\equiv ct-z. Here, t is the ordinary time, z is one Cartesian coordinate system, Cartesian coordinate, and c is the speed of light. The other two Cartesian coordinates, x and y, are untouched and often called transverse or perpendicular, denoted by symbols of the type \vec x_\perp = (x,y). The choice of the frame of reference where the time t and z-axis are defined can be left unspecified in an exactly soluble relativistic theory, but in practical calculations some choices may be m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
World Line
The world line (or worldline) of an object is the path that an object traces in 4- dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics. The concept of a "world line" is distinguished from concepts such as an " orbit" or a " trajectory" (e.g., a planet's ''orbit in space'' or the ''trajectory'' of a car on a road) by the ''time'' dimension, and typically encompasses a large area of spacetime wherein perceptually straight paths are recalculated to show their ( relatively) more absolute position states—to reveal the nature of special relativity or gravitational interactions. The idea of world lines originates in physics and was pioneered by Hermann Minkowski. The term is now most often used in relativity theories (i.e., special relativity and general relativity). Usage in physics In physics, a world line of an object (approximated as a point in space, e.g., a particle or observer) is the sequence of spacetime events corr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SLAC
SLAC National Accelerator Laboratory, originally named the Stanford Linear Accelerator Center, is a United States Department of Energy National Laboratory operated by Stanford University under the programmatic direction of the U.S. Department of Energy Office of Science and located in Menlo Park, California. It is the site of the Stanford Linear Accelerator, a 3.2 kilometer (2-mile) linear accelerator constructed in 1966 and shut down in the 2000s, that could accelerate electrons to energies of 50 GeV. Today SLAC research centers on a broad program in atomic and solid-state physics, chemistry, biology, and medicine using X-rays from synchrotron radiation and a free-electron laser as well as experimental and theoretical research in elementary particle physics, astroparticle physics, and cosmology. History Founded in 1962 as the Stanford Linear Accelerator Center, the facility is located on of Stanford University-owned land on Sand Hill Road in Menlo Park ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Amplitude
In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The modulus squared of this quantity represents a probability density. Probability amplitudes provide a relationship between the quantum state vector of a system and the results of observations of that system, a link was first proposed by Max Born, in 1926. Interpretation of values of a wave function as the probability amplitude is a pillar of the Copenhagen interpretation of quantum mechanics. In fact, the properties of the space of wave functions were being used to make physical predictions (such as emissions from atoms being at certain discrete energies) before any physical interpretation of a particular function was offered. Born was awarded half of the 1954 Nobel Prize in Physics for this understanding, and the probability thus calculated is sometimes called the "Born probability". These probabilistic concepts, namely the probability density and quantum measurem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fock State
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an important role in the second quantization formulation of quantum mechanics. The particle representation was first treated in detail by Paul Dirac for bosons and by Pascual Jordan and Eugene Wigner for fermions. The Fock states of bosons and fermions obey useful relations with respect to the Fock space creation and annihilation operators. Definition One specifies a multiparticle state of N non-interacting identical particles by writing the state as a sum of tensor products of N one-particle states. Additionally, depending on the integrality of the particles' spin, the tensor products must be alternating (anti-symmetric) or symmetric products of the underlying one-particle Hilbert space. Specifically: * Fermions, having half-integer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annihilation
In particle physics, annihilation is the process that occurs when a subatomic particle collides with its respective antiparticle to produce other particles, such as an electron colliding with a positron to produce two photons. The total energy and momentum of the initial pair are conserved in the process and distributed among a set of other particles in the final state. Antiparticles have exactly opposite additive quantum numbers from particles, so the sums of all quantum numbers of such an original pair are zero. Hence, any set of particles may be produced whose total quantum numbers are also zero as long as conservation of energy and conservation of momentum are obeyed. During a low-energy annihilation, photon production is favored, since these particles have no mass. High-energy particle colliders produce annihilations where a wide variety of exotic heavy particles are created. The word "annihilation" takes use informally for the interaction of two particles that are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Creation
Even restricting the discussion to physics, scientists do not have a unique definition of what matter is. In the currently known particle physics, summarised by the standard model of elementary particles and interactions, it is possible to distinguish in an absolute sense particles of matter and particles of antimatter. This is particularly easy for those particles that carry electric charge, such as electrons, protons or quarks, while the distinction is more subtle in the case of neutrinos, fundamental elementary particles that do not carry electric charge. In the standard model, it is not possible to create a net amount of matter particles—or more precisely, it is not possible to change the net number of leptons or of quarks in any perturbative reaction among particles. This remark is consistent with all existing observations. However, similar processes are not considered to be impossible and are expected in other models of the elementary particles, that extend the standard m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called ''color''. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years. QCD exhibits three salient properties: * Color confinement. Due to the force between two color charges remaining constant as they are separated, the energy grows until a quark–antiquark pair is spontaneously produced, turning the initial hadron into a pair of hadrons instead of isolating a color charge. Al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Electrodynamics
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction. In technical terms, QED can be described as a perturbation theory of the electromagnetic quantum vacuum. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. History The first formulation of a quantum theory describing radiation and matter interaction is attributed to British scientist Paul Dirac, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics. Kinematics is used in astrophysics to describe the motion of celestial bodies and collections of such bodies. In mechanical engineering, robotics, and biomechanics kinematics is use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from 1, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Dirac
Paul Adrien Maurice Dirac (; 8 August 1902 – 20 October 1984) was an English theoretical physicist who is regarded as one of the most significant physicists of the 20th century. He was the Lucasian Professor of Mathematics at the University of Cambridge, a professor of physics at Florida State University and the University of Miami, and a 1933 Nobel Prize recipient. Dirac made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics. Among other discoveries, he formulated the Dirac equation which describes the behaviour of fermions and predicted the existence of antimatter. Dirac shared the 1933 Nobel Prize in Physics with Erwin Schrödinger "for the discovery of new productive forms of atomic theory". He also made significant contributions to the reconciliation of general relativity with quantum mechanics. Dirac was regarded by his friends and colleagues as unusual in character. In a 1926 letter to Paul Ehrenfest, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |