|
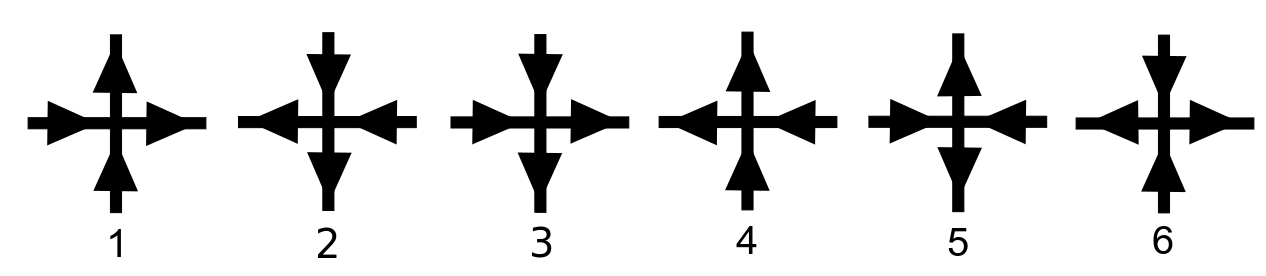
Lieb's Square Ice Constant
Lieb's square ice constant is a mathematical constant used in the field of combinatorics to quantify the number of Eulerian orientations of grid graphs. It was introduced by Elliott H. Lieb in 1967. Definition An ''n'' × ''n'' grid graph (with periodic boundary conditions and ''n'' ≥ 2) has ''n''2 vertices and 2''n''2 edges; it is 4-regular, meaning that each vertex has exactly four neighbors. An orientation of this graph is an assignment of a direction to each edge; it is an Eulerian orientation if it gives each vertex exactly two incoming edges and exactly two outgoing edges. Denote the number of Eulerian orientations of this graph by ''f''(''n''). Then : \lim_\sqrt ^2\left(\frac\right)^\frac=\frac=1.5396007\dots is Lieb's square ice constant. Lieb used a transfer-matrix method to compute this exactly. The function f(n) also counts the number of 3-colorings of grid graphs, the number of nowhere-zero 3-flows in 4-regular graphs, and the number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Constant
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory, statistics, and calculus. What it means for a constant to arise "naturally", and what makes a constant "interesting", is ultimately a matter of taste, with some mathematical constants being notable more for historical reasons than for their intrinsic mathematical interest. The more popular constants have been studied throughout the ages and computed to many decimal places. All named mathematical constants are definable numbers, and usually are also computable numbers ( Chaitin's constant being a significant exception). Basic mathematical constants These are constants which one is likely to encount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Ice
A spin ice is a magnetic substance that does not have a single minimal-energy state. It has magnetic moments (i.e. "spin") as elementary degrees of freedom which are subject to frustrated interactions. By their nature, these interactions prevent the moments from exhibiting a periodic pattern in their orientation down to a temperature much below the energy scale set by the said interactions. Spin ices show low-temperature properties, residual entropy in particular, closely related to those of common crystalline water ice. The most prominent compounds with such properties are dysprosium titanate (Dy2Ti2O7) and holmium titanate (Ho2Ti2O7). The orientation of the magnetic moments in spin ice resembles the positional organization of hydrogen atoms (more accurately, ionized hydrogen, or protons) in conventional water ice (see figure 1). Experiments have found evidence for the existence of deconfined magnetic monopoles in these materials, with properties resembling those of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ice-type Model
In statistical mechanics, the ice-type models or six-vertex models are a family of vertex models for crystal lattices with hydrogen bonds. The first such model was introduced by Linus Pauling in 1935 to account for the residual entropy of water ice. Variants have been proposed as models of certain ferroelectric and antiferroelectric crystals. In 1967, Elliott H. Lieb found the exact solution to a two-dimensional ice model known as "square ice". The exact solution in three dimensions is only known for a special "frozen" state. Description An ice-type model is a lattice model defined on a lattice of coordination number 4. That is, each vertex of the lattice is connected by an edge to four "nearest neighbours". A state of the model consists of an arrow on each edge of the lattice, such that the number of arrows pointing inwards at each vertex is 2. This restriction on the arrow configurations is known as the ice rule. In graph theoretic terms, the states are Eulerian orient ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miura Fold
The is a method of folding a flat surface such as a sheet of paper into a smaller area. The fold is named for its inventor, Japanese astrophysicist Kōryō Miura. The crease patterns of the Miura fold form a tessellation of the surface by parallelograms. In one direction, the creases lie along straight lines, with each parallelogram forming the mirror reflection of its neighbor across each crease. In the other direction, the creases zigzag, and each parallelogram is the translation of its neighbor across the crease. Each of the zigzag paths of creases consists solely of mountain folds or of valley folds, with mountains alternating with valleys from one zigzag path to the next. Each of the straight paths of creases alternates between mountain and valley folds.. Reproduced in ''British Origami'', 1981, and online at the British Origami Society web site. The Miura fold is related to the Kresling fold, the Yoshimura fold and the Hexagonal fold, and can be framed as a genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nowhere-zero Flow
In graph theory, a nowhere-zero flow or NZ flow is a network flow that is nowhere zero. It is intimately connected (by duality) to coloring planar graphs. Definitions Let ''G'' = (''V'',''E'') be a digraph and let ''M'' be an abelian group. A map ''φ'': ''E'' → ''M'' is an ''M''-circulation if for every vertex ''v'' ∈ ''V'' :\sum_ \phi(e) = \sum_ \phi(e), where ''δ''+(''v'') denotes the set of edges out of ''v'' and ''δ''−(''v'') denotes the set of edges into ''v''. Sometimes, this condition is referred to as Kirchhoff's law. If ''φ''(''e'') ≠ 0 for every ''e'' ∈ ''E'', we call ''φ'' a nowhere-zero flow, an ''M''-flow, or an NZ-flow. If ''k'' is an integer and 0 < , ''φ''(''e''), < ''k'' then ''φ'' is a ''k''-flow. Other notions Let ''G'' = (''V'',''E'') be an . An or ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer-matrix Method
In statistical mechanics, the transfer-matrix method is a mathematical technique which is used to write the partition function into a simpler form. It was introduced in 1941 by Hans Kramers and Gregory Wannier. In many one dimensional lattice models, the partition function is first written as an ''n''-fold summation over each possible microstate, and also contains an additional summation of each component's contribution to the energy of the system within each microstate. Overview Higher dimensional models contain even more summations. For systems with more than a few particles, such expressions can quickly become too complex to work out directly, even by computer. Instead, the partition function can be rewritten in an equivalent way. The basic idea is to write the partition function in the form : \mathcal = \mathbf_0 \cdot \left\ \cdot \mathbf_ where v0 and v''N''+1 are vectors of dimension ''p'' and the ''p'' × ''p'' matrices W''k'' are the so-called tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orientation (graph Theory)
In graph theory, an orientation of an undirected graph is an assignment of a direction to each edge, turning the initial graph into a directed graph. Oriented graphs A directed graph is called an oriented graph if none of its pairs of vertices is linked by two symmetric edges. Among directed graphs, the oriented graphs are the ones that have no 2-cycles (that is at most one of and may be arrows of the graph). A tournament is an orientation of a complete graph. A polytree is an orientation of an undirected tree. Sumner's conjecture states that every tournament with vertices contains every polytree with vertices. The number of non-isomorphic oriented graphs with vertices (for ) is : 1, 2, 7, 42, 582, 21480, 2142288, 575016219, 415939243032, … . Tournaments are in one-to-one correspondence with complete directed graphs (graphs in which there is a directed edge in one or both directions between every pair of distinct vertices). A complete directed graph can be converted to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree is called a graph or regular graph of degree . Also, from the handshaking lemma, a regular graph contains an even number of vertices with odd degree. Regular graphs of degree at most 2 are easy to classify: a graph consists of disconnected vertices, a graph consists of disconnected edges, and a graph consists of a disjoint union of cycles and infinite chains. A graph is known as a cubic graph. A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number of neighbors in common, and every non-adjacent pair of vertices has the same number of neighbors in common. The smallest graphs that are regular but not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Boundary Conditions
Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a ''unit cell''. PBCs are often used in computer simulations and mathematical models. The topology of two-dimensional PBC is equal to that of a ''world map'' of some video games; the geometry of the unit cell satisfies perfect two-dimensional tiling, and when an object passes through one side of the unit cell, it re-appears on the opposite side with the same velocity. In topological terms, the space made by two-dimensional PBCs can be thought of as being mapped onto a torus (compactification). The large systems approximated by PBCs consist of an infinite number of unit cells. In computer simulations, one of these is the original simulation box, and others are copies called ''images''. During the simulation, only the properties of the original simulation box need to be recorded and propagated. The ''minimum-image conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |