|
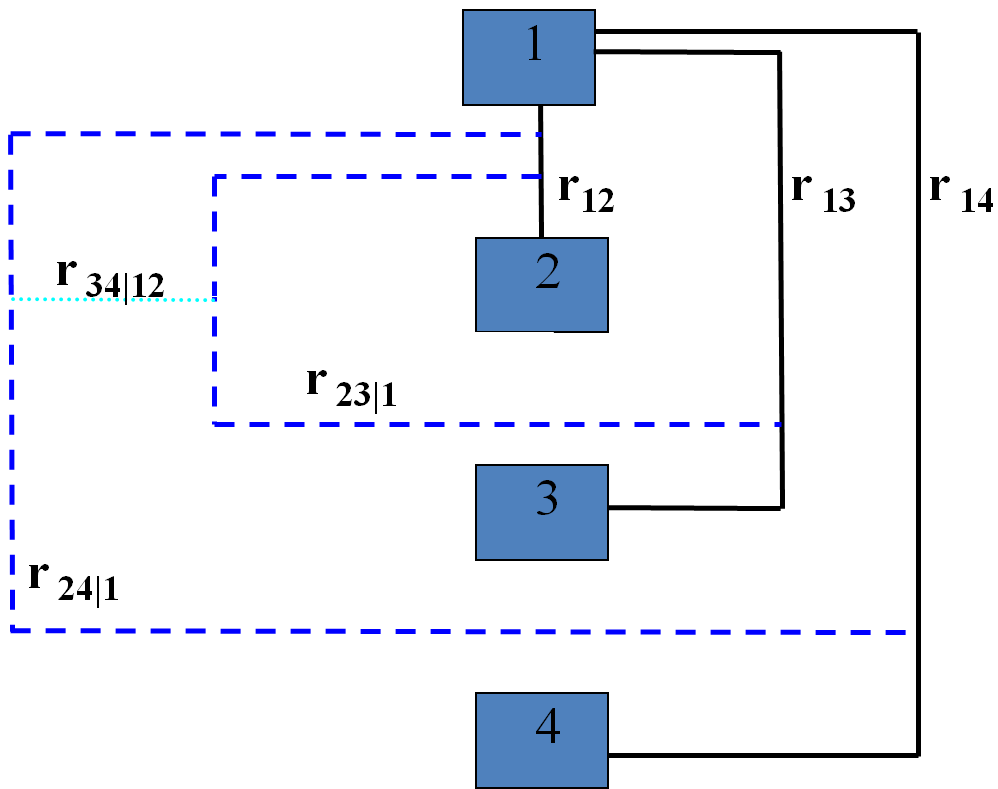
Lewandowski-Kurowicka-Joe Distribution
In probability theory and Bayesian statistics, the Lewandowski-Kurowicka-Joe distribution, often referred to as the LKJ distribution, is a probability distribution over positive definite symmetric matrices with unit diagonals. Introduction The LKJ distribution was first introduced in 2009 in a more general context by Daniel Lewandowski, Dorota Kurowicka, and Harry Joe. It is an example of the vine copula, an approach to constrained high-dimensional probability distributions. The distribution has a single shape parameter \eta and the probability density function for a d\times d matrix \mathbf is :p(\mathbf; \eta) = C \times det(\mathbf) with normalizing constant C=2^\prod_^\left \left(\eta + (d-k-1)/2, \eta + (d-k-1)/2\right)\right, a complicated expression including a product over Beta functions. For \eta=1, the distribution is uniform over the space of all correlation matrices; i.e. the space of positive definite matrices with unit diagonal. Usage The LKJ distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation that views probability as the limit of the relative frequency of an event after many trials. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can be used to estimate the parameters of a probability distribution or statistical model. Since Bayesian statistics treats probabi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it defines a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vine Copula
A vine is a graphical tool for labeling constraints in high-dimensional probability distributions. A regular vine is a special case for which all constraints are two-dimensional or conditional two-dimensional. Regular vines generalize trees, and are themselves specializations of Cantor tree. Combined with bivariate copulas, regular vines have proven to be a flexible tool in high-dimensional dependence modeling. Copulas are multivariate distributions with uniform univariate margins. Representing a joint distribution as univariate margins plus copulas allows the separation of the problems of estimating univariate distributions from the problems of estimating dependence. This is handy in as much as univariate distributions in many cases can be adequately estimated from data, whereas dependence information is rough known, involving summary indicators and judgment. Although the number of parametric multivariate copula families with flexible dependence is limited, there are many parametr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral : \Beta(z_1,z_2) = \int_0^1 t^(1-t)^\,dt for complex number inputs z_1, z_2 such that \Re(z_1), \Re(z_2)>0. The beta function was studied by Leonhard Euler and Adrien-Marie Legendre and was given its name by Jacques Binet; its symbol is a Greek capital beta. Properties The beta function is symmetric, meaning that \Beta(z_1,z_2) = \Beta(z_2,z_1) for all inputs z_1 and z_2.Davis (1972) 6.2.2 p.258 A key property of the beta function is its close relationship to the gamma function: : \Beta(z_1,z_2)=\frac. A proof is given below in . The beta function is also closely related to binomial coefficients. When (or , by symmetry) is a positive integer, it follows from the definition of the gamma function thatDavis (1972) 6.2.1 p.258 : \Beta(m,n) =\dfrac = \frac \B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse-Wishart Distribution
In statistics, the inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution defined on real-valued positive-definite matrices. In Bayesian statistics it is used as the conjugate prior for the covariance matrix of a multivariate normal distribution. We say \mathbf follows an inverse Wishart distribution, denoted as \mathbf\sim \mathcal^(\mathbf\Psi,\nu), if its inverse \mathbf^ has a Wishart distribution \mathcal(\mathbf \Psi^, \nu) . Important identities have been derived for the inverse-Wishart distribution. Density The probability density function of the inverse Wishart is: : f_(; , \nu) = \frac \left, \mathbf\^ e^ where \mathbf and are p\times p positive definite matrices, , \cdot , is the determinant, and Γ''p''(·) is the multivariate gamma function. Theorems Distribution of the inverse of a Wishart-distributed matrix If \sim \mathcal(,\nu) and is of size p \times p, then \mathbf=^ has an inverse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stan (software)
Stan is a probabilistic programming language for statistical inference written in C++.Stan Development Team. 2015Stan Modeling Language User's Guide and Reference Manual, Version 2.9.0/ref> The Stan language is used to specify a (Bayesian) statistical model with an imperative program calculating the log probability density function. Stan is licensed under the New BSD License. Stan is named in honour of Stanislaw Ulam, pioneer of the Monte Carlo method. Stan was created by a development team consisting of 34 members that includes Andrew Gelman, Bob Carpenter, Matt Hoffman, and Daniel Lee. Interfaces The Stan language itself can be accessed through several interfaces: * CmdStan – a command-line executable for the shell, * CmdStanR and rstan – R software libraries, * CmdStanPy and PyStan – libraries for the Python programming language, * MatlabStan – integration with the MATLAB numerical computing environment, * Stan.jl – integration with the Julia programming langua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probabilistic Programming Language
Probabilistic programming (PP) is a programming paradigm in which probabilistic models are specified and inference for these models is performed automatically. It represents an attempt to unify probabilistic modeling and traditional general purpose programming in order to make the former easier and more widely applicable.Pfeffer, Avrom (2014), ''Practical Probabilistic Programming'', Manning Publications. p.28. It can be used to create systems that help make decisions in the face of uncertainty. Programming languages used for probabilistic programming are referred to as "probabilistic programming languages" (PPLs). Applications Probabilistic reasoning has been used for a wide variety of tasks such as predicting stock prices, recommending movies, diagnosing computers, detecting cyber intrusions and image detection. However, until recently (partially due to limited computing power), probabilistic programming was limited in scope, and most inference algorithms had to be written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing (software)
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher, and theoretical biologist. Turing was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. He is widely considered to be the father of theoretical computer science and artificial intelligence. Born in Maida Vale, London, Turing was raised in southern England. He graduated at King's College, Cambridge, with a degree in mathematics. Whilst he was a fellow at Cambridge, he published a proof demonstrating that some purely mathematical yes–no questions can never be answered by computation and defined a Turing machine, and went on to prove that the halting problem for Turing machines is undecidable. In 1938, he obtained his PhD from the Department o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julia (programming Language)
Julia is a high-level, dynamic programming language. Its features are well suited for numerical analysis and computational science. Distinctive aspects of Julia's design include a type system with parametric polymorphism in a dynamic programming language; with multiple dispatch as its core programming paradigm. Julia supports concurrent, (composable) parallel and distributed computing (with or without using MPI or the built-in corresponding to "OpenMP-style" threads), and direct calling of C and Fortran libraries without glue code. Julia uses a just-in-time (JIT) compiler that is referred to as "just- ahead-of-time" (JAOT) in the Julia community, as Julia compiles all code (by default) to machine code before running it. Julia is garbage-collected, uses eager evaluation, and includes efficient libraries for floating-point calculations, linear algebra, random number generation, and regular expression matching. Many libraries are available, including some (e.g., for fast Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |