|
Laplace Motion
In the theory of stochastic processes, a part of the mathematical theory of probability, the variance gamma process (VG), also known as Laplace motion, is a Lévy process determined by a random time change. The process has finite moments distinguishing it from many Lévy processes. There is no diffusion component in the VG process and it is thus a pure jump process. The increments are independent and follow a variance-gamma distribution, which is a generalization of the Laplace distribution. There are several representations of the VG process that relate it to other processes. It can for example be written as a Brownian motion W(t) with drift \theta t subjected to a random time change which follows a gamma process \Gamma(t; 1, \nu) (equivalently one finds in literature the notation \Gamma(t;\gamma=1/\nu,\lambda=1/\nu)): : X^(t; \sigma, \nu, \theta) \;:=\; \theta \,\Gamma(t; 1, \nu) + \sigma\,W(\Gamma(t; 1, \nu)) \quad. An alternative way of stating this is that the varianc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kurtosis
In probability theory and statistics, kurtosis (from el, κυρτός, ''kyrtos'' or ''kurtos'', meaning "curved, arching") is a measure of the "tailedness" of the probability distribution of a real-valued random variable. Like skewness, kurtosis describes a particular aspect of a probability distribution. There are different ways to quantify kurtosis for a theoretical distribution, and there are corresponding ways of estimating it using a sample from a population. Different measures of kurtosis may have different interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as "peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configuration of data near the mean. It is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
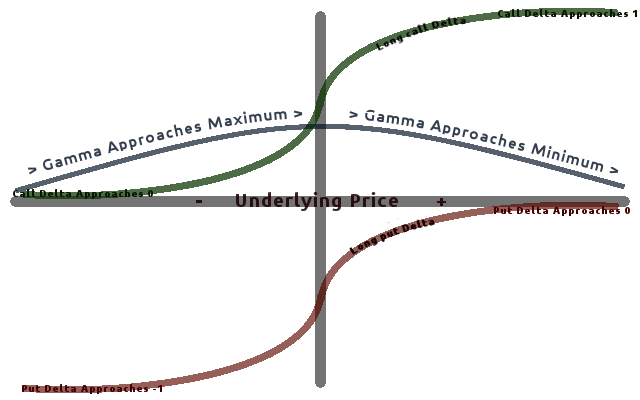
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2-EPT Probability Density Function
In probability theory, a 2-EPT probability density function is a class of probability density functions on the real line. The class contains the density functions of all distributions that have characteristic functions that are strictly proper rational functions (i.e., the degree of the numerator is strictly less than the degree of the denominator). Definition A 2-EPT probability density function is a probability density function on \mathbb with a strictly proper rational characteristic function. On either [0, +\infty) or (-\infty, 0) these probability density functions are exponential-polynomial-trigonometric (EPT) functions. Any EPT density function on (-\infty, 0) can be represented as :f(x)=\textbf_Ne^\textbf_N , where ''e'' represents a matrix exponential, (\textbf_N,\textbf_P) are square matrices, (\textbf_N,\textbf_P) are column vectors and (\textbf_N,\textbf_P) are row vectors. Similarly the EPT density function on [0, -\infty) is expressed as :f(x)=\textbf_Pe^\textbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Credit Default Swap
A credit default swap (CDS) is a financial swap agreement that the seller of the CDS will compensate the buyer in the event of a debt default (by the debtor) or other credit event. That is, the seller of the CDS insures the buyer against some reference asset defaulting. The buyer of the CDS makes a series of payments (the CDS "fee" or "spread") to the seller and, in exchange, may expect to receive a payoff if the asset defaults. In the event of default, the buyer of the credit default swap receives compensation (usually the face value of the loan), and the seller of the CDS takes possession of the defaulted loan or its market value in cash. However, anyone can purchase a CDS, even buyers who do not hold the loan instrument and who have no direct insurable interest in the loan (these are called "naked" CDSs). If there are more CDS contracts outstanding than bonds in existence, a protocol exists to hold a credit event auction. The payment received is often substantially less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Credit Risk
A credit risk is risk of default on a debt that may arise from a borrower failing to make required payments. In the first resort, the risk is that of the lender and includes lost principal and interest, disruption to cash flows, and increased collection costs. The loss may be complete or partial. In an efficient market, higher levels of credit risk will be associated with higher borrowing costs. Because of this, measures of borrowing costs such as yield spreads can be used to infer credit risk levels based on assessments by market participants. Losses can arise in a number of circumstances, for example: * A consumer may fail to make a payment due on a mortgage loan, credit card, line of credit, or other loan. * A company is unable to repay asset-secured fixed or floating charge debt. * A business or consumer does not pay a trade invoice when due. * A business does not pay an employee's earned wages when due. * A business or government bond issuer does not make a payment on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asian Option
An Asian option (or ''average value'' option) is a special type of option contract. For Asian options the payoff is determined by the average underlying price over some pre-set period of time. This is different from the case of the usual European option and American option, where the payoff of the option contract depends on the price of the underlying instrument at exercise; Asian options are thus one of the basic forms of exotic options. There are two types of Asian options: fixed strike, where averaging price is used in place of underlying price; and fixed price, where averaging price is used in place of strike. One advantage of Asian options is that these reduce the risk of market manipulation of the underlying instrument at maturity. Another advantage of Asian options involves the relative cost of Asian options compared to European or American options. Because of the averaging feature, Asian options reduce the volatility inherent in the option; therefore, Asian options are typic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Computational Finance
''The Journal of Computational Finance'' is a peer-reviewed academic journal, published five times per year, covering advances in numerical and computational techniques in pricing, hedging, and risk management of financial instruments. It was established in 1997 and is published by Infopro Digital as part of theiRisk Journalsportfolio. The editor-in-chief is Christoph Reisinger (Mathematical Institute, University of Oxford). According to the ''Journal Citation Reports'', the journal has a 2015 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as i ... of 0.758. References External links * Finance journals Publications established in 1997 English-language journals Quarterly journals {{Computer-science-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Option
In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as "vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging. American and European options The key difference between American and European options relates to when the options can be exercised: * A European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time. * An American option on the other hand may be exercised at any time before the expiration date. For both, the payoff—when it occurs—is given by * \max\, for a call option * \max\, for a put option where K is the strike pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
European Option
In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as "vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging. American and European options The key difference between American and European options relates to when the options can be exercised: * A European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time. * An American option on the other hand may be exercised at any time before the expiration date. For both, the payoff—when it occurs—is given by * \max\, for a call option * \max\, for a put option where K is the strike pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Business
''The Journal of Business'' was an academic journal published by the University of Chicago Press The University of Chicago Press is the largest and one of the oldest university presses in the United States. It is operated by the University of Chicago and publishes a wide variety of academic titles, including ''The Chicago Manual of Style'', .... It aimed to cover "a comprehensive range of areas, including business finance and investment, money and banking, marketing, security markets, business economics, accounting practices, social issues and public policy, management organization, statistics and econometrics, administration and management, international trade and finance, and personnel, industrial relations, and labor." Originally titled ''The Journal of Business of the University of Chicago'' when it debuted in 1928, the journal shortened its name to ''The Journal of Business'' in 1954. Its broad scope became a liability as specialization in business scholarship grew and num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas). This pattern of motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the equipartition theorem). This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking throu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
