|
Langlands Classification
In mathematics, the Langlands classification is a description of the irreducible representations of a reductive Lie group ''G'', suggested by Robert Langlands (1973). There are two slightly different versions of the Langlands classification. One of these describes the irreducible Admissible representation, admissible (''g'', ''K'')-module (mathematics), modules, for ''g'' a Lie algebra of a reductive Lie group ''G'', with maximal compact subgroup ''K'', in terms of tempered representations of smaller groups. The tempered representations were in turn classified by Anthony W. Knapp, Anthony Knapp and Gregg Zuckerman. The other version of the Langlands classification divides the irreducible representations into L-packets, and classifies the L-packets in terms of certain homomorphisms of the Weil group of R or C into the Langlands dual group. Notation *''g'' is the Lie algebra of a real reductive Lie group ''G'' in the Harish-Chandra class. *''K'' is a maximal compact subgroup of ''G'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Dual Group
In representation theory, a branch of mathematics, the Langlands dual ''L''''G'' of a reductive algebraic group ''G'' (also called the ''L''-group of ''G'') is a group that controls the representation theory of ''G''. If ''G'' is defined over a field ''k'', then ''L''''G'' is an extension of the absolute Galois group of ''k'' by a complex Lie group. There is also a variation called the Weil form of the ''L''-group, where the Galois group is replaced by a Weil group. Here, the letter ''L'' in the name also indicates the connection with the theory of L-functions, particularly the ''automorphic'' L-functions. The Langlands dual was introduced by in a letter to A. Weil. The ''L''-group is used heavily in the Langlands conjectures of Robert Langlands. It is used to make precise statements from ideas that automorphic forms are in a sense functorial in the group ''G'', when ''k'' is a global field. It is not exactly ''G'' with respect to which automorphic forms and representations are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nolan Wallach
Nolan Russell Wallach (born August 3, 1940) is a mathematician known for work in the representation theory of reductive algebraic groups. He is the author of the two-volume treatise ''Real Reductive Groups''. Education and career Wallach did his undergraduate studies at the University of Maryland, graduating in 1962.UCSD Mathematics Profile: Nolan Wallach , retrieved 2013-09-01. He earned his Ph.D. from in 1966, under the supervision of Jun-Ichi Hano. He became an instructor and then lecturer at the |
Armand Borel
Armand Borel (21 May 1923 – 11 August 2003) was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993. He worked in algebraic topology, in the theory of Lie groups, and was one of the creators of the contemporary theory of linear algebraic groups. Biography He studied at the ETH Zürich, where he came under the influence of the topologist Heinz Hopf and Lie-group theorist Eduard Stiefel. He was in Paris from 1949: he applied the Leray spectral sequence to the topology of Lie groups and their classifying spaces, under the influence of Jean Leray and Henri Cartan. With Hirzebruch, he significantly developed the theory of characteristic classes in the early 1950s. He collaborated with Jacques Tits in fundamental work on algebraic groups, and with Harish-Chandra on their arithmetic subgroups. In an algebraic group ''G'' a '' Borel subgroup'' ''H'' is one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory Of SL2(R)
In mathematics, the main results concerning irreducible unitary representations of the Lie group SL(2, R) are due to Gelfand and Naimark (1946), V. Bargmann (1947), and Harish-Chandra (1952). Structure of the complexified Lie algebra We choose a basis ''H'', ''X'', ''Y'' for the complexification of the Lie algebra of SL(2, R) so that ''iH'' generates the Lie algebra of a compact Cartan subgroup ''K'' (so in particular unitary representations split as a sum of eigenspaces of ''H''), and is an sl2-triple, which means that they satisfy the relations : ,X2X, \quad ,Y-2Y, \quad ,YH. One way of doing this is as follows: :H=\begin0 & -i\\ i & 0\end corresponding to the subgroup ''K'' of matrices \begin\cos(\theta) & -\sin(\theta)\\ \sin(\theta)& \cos(\theta)\end :X=\begin1 & i\\ i & -1\end :Y=\begin1 & -i\\ -i & -1\end The Casimir operator Ω is defined to be :\Omega= H^2+1+2XY+2YX. It generates the center of the universal enveloping algebra of the complexified Lie algeb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup ''P'' of a semisimple Lie group as a product P=MAN of a reductive subgroup ''M'', an abelian subgroup ''A'', and a nilpotent subgroup ''N''. Applications A key application is in parabolic induction, which leads to the Langlands program In mathematics, the Langlands program is a set of conjectures about connections between number theory, the theory of automorphic forms, and geometry. It was proposed by . It seeks to relate the structure of Galois groups in algebraic number t ...: if G is a reductive algebraic group and P=MAN is the Langlands decomposition of a parabolic subgroup ''P'', then parabolic induction consists of taking a representation of MA, extending it to P by letting N act trivially, and inducing the result from P to G. See also * Lie group decompositions References Sources * A. W. Knapp, Structure theory of semisimple Lie groups. . Lie groups Algebraic groups {{Mathan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borel Subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group ''G'' is a maximal Zariski closed and connected solvable algebraic subgroup. For example, in the general linear group ''GLn'' (''n x n'' invertible matrices), the subgroup of invertible upper triangular matrices is a Borel subgroup. For groups realized over algebraically closed fields, there is a single conjugacy class of Borel subgroups. Borel subgroups are one of the two key ingredients in understanding the structure of simple (more generally, reductive) algebraic groups, in Jacques Tits' theory of groups with a (''B'', ''N'') pair. Here the group ''B'' is a Borel subgroup and ''N'' is the normalizer of a maximal torus contained in ''B''. The notion was introduced by Armand Borel, who played a leading role in the development of the theory of algebraic groups. Parabolic subgroups Subgroups between a Borel subgroup ''B'' and the ambient group ''G'' are called parabolic subgroups. Parabolic subgr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Admissible Representation
In mathematics, admissible representations are a well-behaved class of Group representation, representations used in the representation theory of reductive group, reductive Lie groups and locally compact group, locally compact totally disconnected groups. They were introduced by Harish-Chandra. Real or complex reductive Lie groups Let ''G'' be a connected reductive (real or complex) Lie group. Let ''K'' be a maximal compact subgroup. A continuous representation (π, ''V'') of ''G'' on a complex Hilbert space ''V''I.e. a homomorphism (where GL(''V'') is the group of bounded linear operators on ''V'' whose inverse is also bounded and linear) such that the associated map is continuous. is called admissible if π restricted to ''K'' is unitary representation, unitary and each irreducible representation, irreducible unitary representation of ''K'' occurs in it with finite multiplicity. The prototypical example is that of an irreducible unitary representation of ''G''. An admissib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
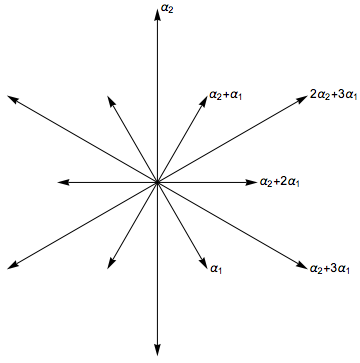
Simple Root (root System)
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors span the whole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root System
In mathematics, a root system is a configuration of vector space, vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors Li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartan Involution
In mathematics, the Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition or singular value decomposition of matrices. Its history can be traced to the 1880s work of Élie Cartan and Wilhelm Killing. Cartan involutions on Lie algebras Let \mathfrak be a real semisimple Lie algebra and let B(\cdot,\cdot) be its Killing form. An involution on \mathfrak is a Lie algebra automorphism \theta of \mathfrak whose square is equal to the identity. Such an involution is called a ''Cartan involution'' on \mathfrak if B_\theta(X,Y) := -B(X,\theta Y) is a positive definite bilinear form. Two involutions \theta_1 and \theta_2 are considered equivalent if they differ only by an inner automorphism. Any real semisimple Lie algebra has a Cartan involution, and any two Cartan involutions are equivalent. Examples * A Cartan involution on \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harish-Chandra Class
In mathematics, Harish-Chandra's class is a class of Lie groups used in representation theory. Harish-Chandra's class contains all semisimple connected linear Lie groups and is closed under natural operations, most importantly, the passage to Levi subgroups. This closure property is crucial for many inductive arguments in representation theory of Lie groups, whereas the classes of semisimple or connected semisimple Lie groups are not closed in this sense. Definition A Lie group ''G'' with the Lie algebra ''g'' is said to be in Harish-Chandra's class if it satisfies the following conditions: *''g'' is a reductive Lie algebra (the product of a semisimple and abelian Lie algebra). *The Lie group ''G'' has only a finite number of connected components. *The adjoint action of any element of ''G'' on ''g'' is given by an action of an element of the connected component of the Lie group of Lie algebra automorphisms of the complexification In mathematics, the complexification of a vect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |