|
L-functions
In mathematics, an ''L''-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An ''L''-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an ''L''-function via analytic continuation. The Riemann zeta function is an example of an ''L''-function, and one important conjecture involving ''L''-functions is the Riemann hypothesis and its generalization. The theory of ''L''-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the ''L''-series for a Dirichlet character are constructed, and their general properties, in most cases still out of reach of proof, are set out in a systematic way. Because of the Euler product formula there is a deep connection between ''L''-functions and the theory of prime numbers. The mathematical field that studies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-adic L-function
In mathematics, a ''p''-adic zeta function, or more generally a ''p''-adic ''L''-function, is a function analogous to the Riemann zeta function, or more general ''L''-functions, but whose domain and target are ''p-adic'' (where ''p'' is a prime number). For example, the domain could be the ''p''-adic integers Z''p'', a profinite ''p''-group, or a ''p''-adic family of Galois representations, and the image could be the ''p''-adic numbers Q''p'' or its algebraic closure. The source of a ''p''-adic ''L''-function tends to be one of two types. The first source—from which Tomio Kubota and Heinrich-Wolfgang Leopoldt gave the first construction of a ''p''-adic ''L''-function —is via the ''p''-adic interpolation of special values of ''L''-functions. For example, Kubota–Leopoldt used Kummer's congruences for Bernoulli numbers to construct a ''p''-adic ''L''-function, the ''p''-adic Riemann zeta function ζ''p''(''s''), whose values at negative odd integers are those of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
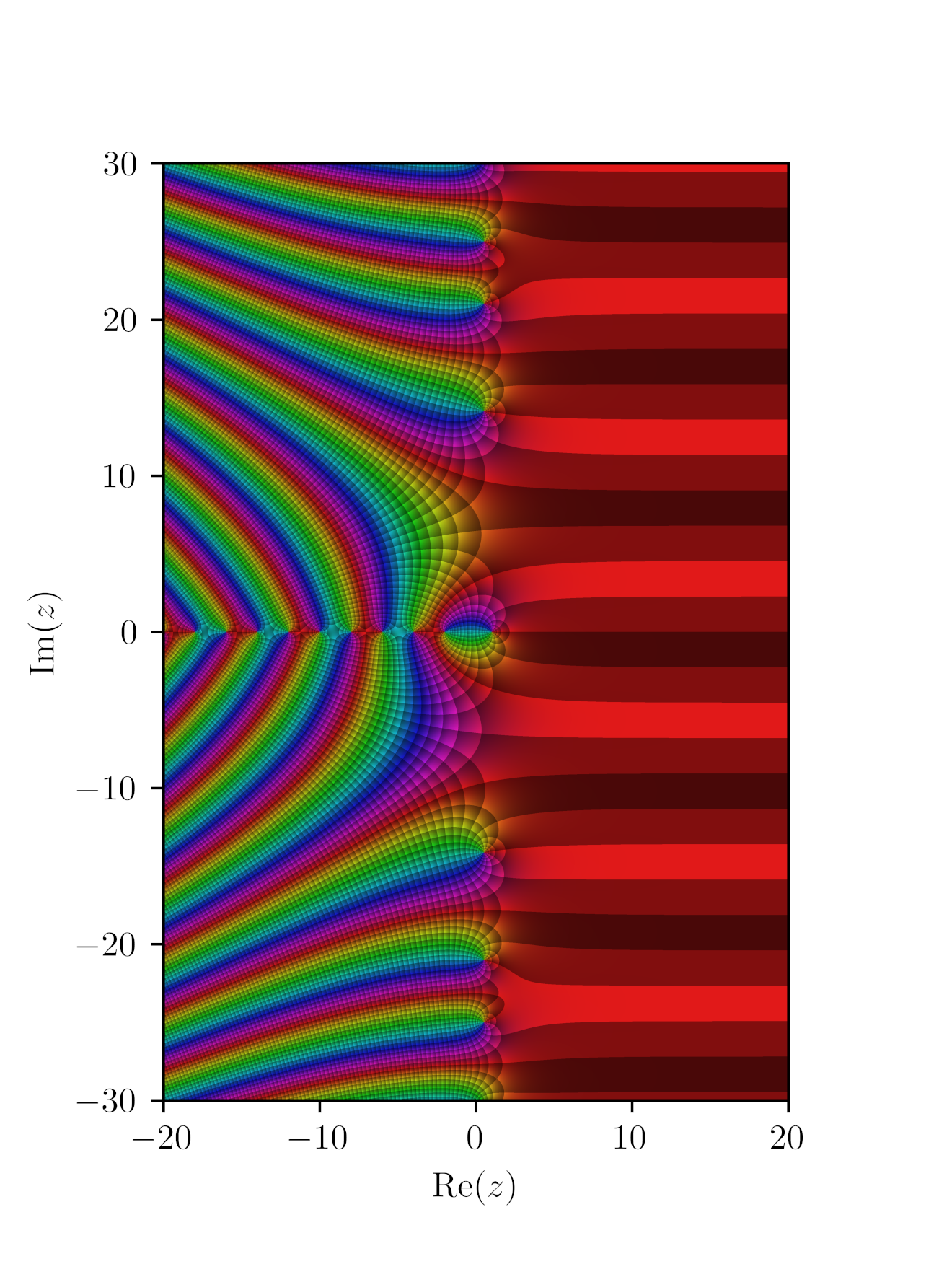
Riemann Hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by , after whom it is named. The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems, which offers a million dollars to anyone who solves any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields. The Riemann zeta function ζ(''s'') is a function whose argument ''s'' may be any complex number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Character
In analytic number theory and related branches of mathematics, a complex-valued arithmetic function \chi:\mathbb\rightarrow\mathbb is a Dirichlet character of modulus m (where m is a positive integer) if for all integers a and b: :1) \chi(ab) = \chi(a)\chi(b); i.e. \chi is completely multiplicative. :2) \chi(a) \begin =0 &\text\; \gcd(a,m)>1\\ \ne 0&\text\;\gcd(a,m)=1. \end (gcd is the greatest common divisor) :3) \chi(a + m) = \chi(a); i.e. \chi is periodic with period m. The simplest possible character, called the principal character, usually denoted \chi_0, (see Notation below) exists for all moduli: : \chi_0(a)= \begin 0 &\text\; \gcd(a,m)>1\\ 1 &\text\;\gcd(a,m)=1. \end The German mathematician Peter Gustav Lejeune Dirichlet—for whom the character is named—introduced these functions in his 1837 paper on primes in arithmetic progressions. Notation \phi(n) is Euler's totient function. \zeta_n is a complex primitive n-th root of uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet L-function
In mathematics, a Dirichlet ''L''-series is a function of the form :L(s,\chi) = \sum_^\infty \frac. where \chi is a Dirichlet character and ''s'' a complex variable with real part greater than 1. It is a special case of a Dirichlet series. By analytic continuation, it can be extended to a meromorphic function on the whole complex plane, and is then called a Dirichlet ''L''-function and also denoted ''L''(''s'', ''χ''). These functions are named after Peter Gustav Lejeune Dirichlet who introduced them in to prove the theorem on primes in arithmetic progressions that also bears his name. In the course of the proof, Dirichlet shows that is non-zero at ''s'' = 1. Moreover, if ''χ'' is principal, then the corresponding Dirichlet ''L''-function has a simple pole at ''s'' = 1. Otherwise, the ''L''-function is entire. Euler product Since a Dirichlet character ''χ'' is completely multiplicative, its ''L''-function can also be written as an Euler product in the half-plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ( zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article " On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selberg Class
In mathematics, the Selberg class is an axiomatic definition of a class of ''L''-functions. The members of the class are Dirichlet series which obey four axioms that seem to capture the essential properties satisfied by most functions that are commonly called ''L''-functions or zeta functions. Although the exact nature of the class is conjectural, the hope is that the definition of the class will lead to a classification of its contents and an elucidation of its properties, including insight into their relationship to automorphic forms and the Riemann hypothesis. The class was defined by Atle Selberg in , who preferred not to use the word "axiom" that later authors have employed. Definition The formal definition of the class ''S'' is the set of all Dirichlet series :F(s)=\sum_^\infty \frac absolutely convergent for Re(''s'') > 1 that satisfy four axioms (or assumptions as Selberg calls them): Comments on definition The condition that the real part of μ''i'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Riemann Hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-function, ''L''-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these ''L''-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case (not the number field case). Global ''L''-functions can be associated to elliptic curves, number fields (in which case they are called Dedekind zeta-functions), Maass forms, and Dirichlet characters (in which case they are called Dirichlet L-series, Dirichlet L-functions). When the Riemann hypothesis is formulated for Dedekind zeta-functions, it is known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural. Introduction A prototypical example, the Riemann zeta function has a functional equation relating its value at the complex number ''s'' with its value at 1 − ''s''. In every case this relates to some value ζ(''s'') that is only defined by analytic continuation from the infinite series definition. That is, writingas is conventionalσ for the real part of ''s'', the functional equation relates the cases :σ > 1 and σ < 0, and also changes a case with :0 < σ < 1 in the ''critical strip'' to another such case, reflected in the line σ = ½. Therefore, use of the functional equation is basic, in order to study the zeta-function in the whole |
Galois Module
In mathematics, a Galois module is a ''G''-module, with ''G'' being the Galois group of some extension of fields. The term Galois representation is frequently used when the ''G''-module is a vector space over a field or a free module over a ring in representation theory, but can also be used as a synonym for ''G''-module. The study of Galois modules for extensions of local or global fields and their group cohomology is an important tool in number theory. Examples *Given a field ''K'', the multiplicative group (''Ks'')× of a separable closure of ''K'' is a Galois module for the absolute Galois group. Its second cohomology group is isomorphic to the Brauer group of ''K'' (by Hilbert's theorem 90, its first cohomology group is zero). *If ''X'' is a smooth proper scheme over a field ''K'' then the ℓ-adic cohomology groups of its geometric fibre are Galois modules for the absolute Galois group of ''K''. Ramification theory Let ''K'' be a valued field (with valuat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic K-theory
Algebraic ''K''-theory is a subject area in mathematics with connections to geometry, topology, ring theory, and number theory. Geometric, algebraic, and arithmetic objects are assigned objects called ''K''-groups. These are groups in the sense of abstract algebra. They contain detailed information about the original object but are notoriously difficult to compute; for example, an important outstanding problem is to compute the ''K''-groups of the integers. ''K''-theory was discovered in the late 1950s by Alexander Grothendieck in his study of intersection theory on algebraic varieties. In the modern language, Grothendieck defined only ''K''0, the zeroth ''K''-group, but even this single group has plenty of applications, such as the Grothendieck–Riemann–Roch theorem. Intersection theory is still a motivating force in the development of (higher) algebraic ''K''-theory through its links with motivic cohomology and specifically Chow groups. The subject also includes class ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Numbers
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Number Theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet ''L''-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers (involving the Prime Number Theorem and Riemann zeta function) and additive number theory (such as the Goldbach conjecture and Waring's problem). Branches of analytic number theory Analytic number theory can be split up into two major parts, divided more by the type of problems they attempt to solve than fundamental differences in technique. * Multiplicative number theory deals with the distribution of the prime numbers, such as estimating the number of primes in an interval, and includes the prime number theorem and Dirichlet's theorem on primes in arithmetic progressions. * Additive n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |